主页
搜索
最近更新
数据统计
申请密钥
系统公告
1
/
1
请查看完所有公告
从压缩 trie 到 SAM
最后更新于 2025-07-31 10:09:16
作者
UKBwyx
分类
算法·理论
复制 Markdown
查看原文
删除文章
更新内容
让我们直入主题吧。 ## 压缩 trie 或许这里的压缩 trie 并不是很标准的压缩 trie。 众所周知,假设你要插入 $n$ 个字符串 $s_i$ 到一个 trie 里,假设字符集大小为 $k$, 通常的写法是时空复杂度 $O(k\sum s_i)$ 的,关键在于建立的节点个数是 $O(\sum s_i)$ 的,这样不够好,我们可以考虑这颗字典树每个字符串结尾节点建出的虚树,这样可以把节点个数压缩成 $O(n)$ 个,时空压成 $O(kn+\sum s_i)$,其中 $kn$ 用来记录节点的每种字符开头的出边,$\sum s_i$ 记录所有边。 或者如果你无法理解,可以先看个例子对比一下。 考虑将 $aab$,$abca$,$abaa$,$abbaa$ 建出一颗**普通 trie**,它应该长这样。 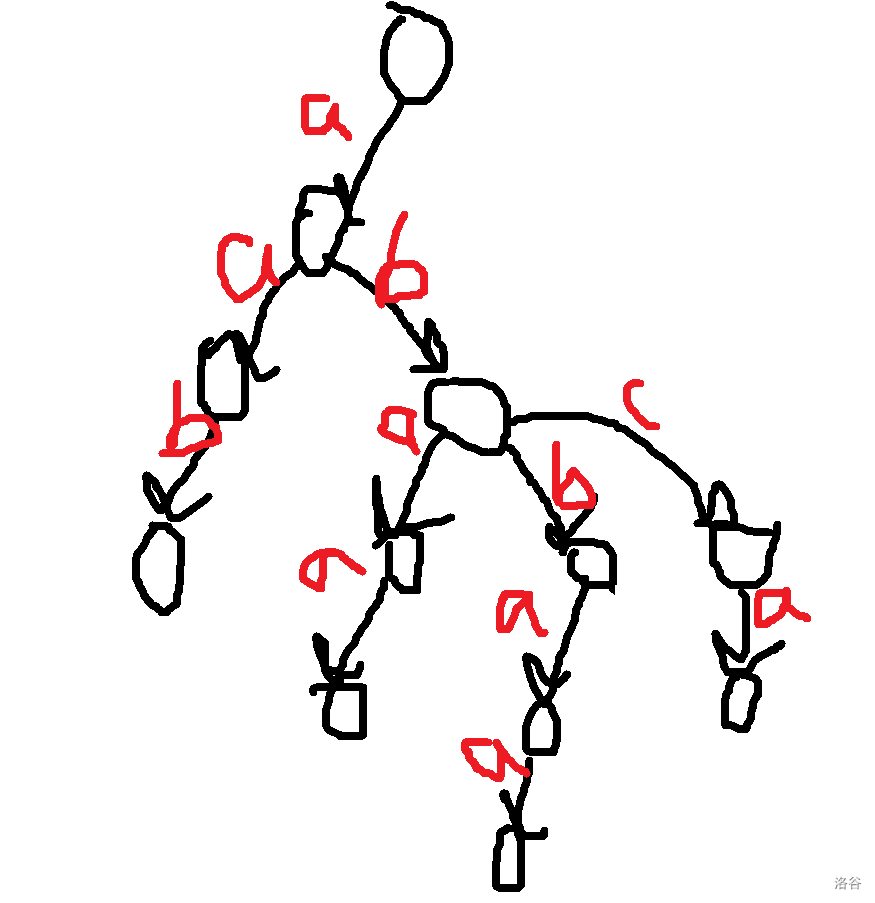 而如果把它们建出一颗**压缩 trie**,则长这样。 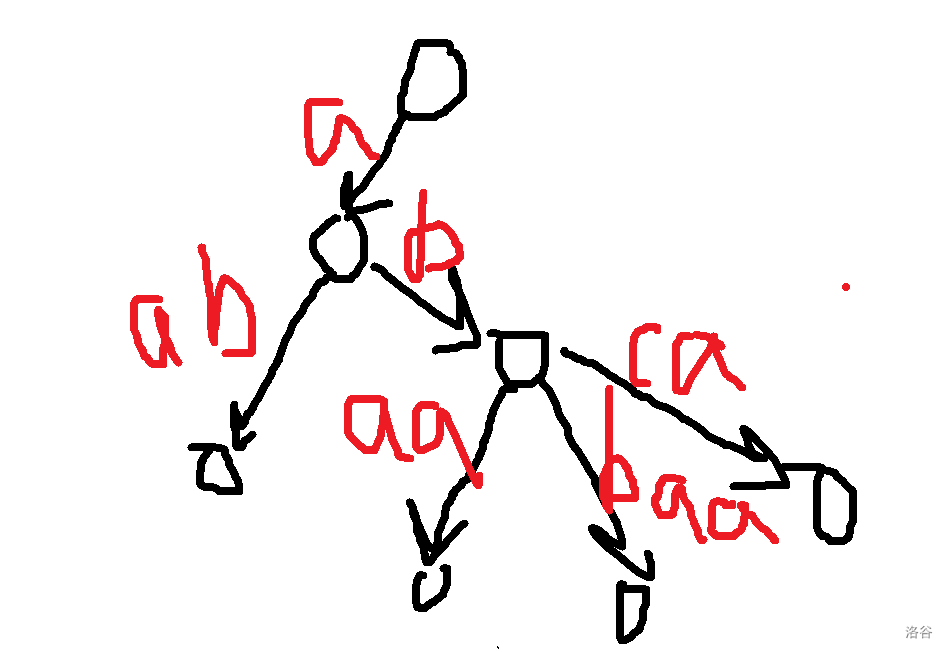 它的核心的思路在于把一条链压缩成一条边。 **需要注意的是,通常来说,压缩 trie 某个字符串的终止节点不能省**。 然后就没了,具体实现可以自己想想,这里懒得说了。 如果仔细想想可以发现,如果能够以很低的空间存储 $\sum s_i$,并支持比较,空间可以降到 $O(kn)$,如果还能用一些神秘方法降低时间复杂度就完成了。 压缩 trie 能实现而普通 trie 不能实现的根本原因是普通 trie 有 $\sum s_i$ 个节点,所以压缩 trie 做到的主要是减少了节点个数。 ## SAM(可能吧) **注意:如果你以前学过 SAM,那么这里的 SAM 的讲法可能和其他的很不一样。** 然后考虑这样一个问题: 你有一个字符串 $s$,初始为空,你要在线完成 $m$ 次以下操作: 操作 1:在 $s$ 的末尾加上一个字符 $c$。 操作 2:给你一个字符串 $t$,判断 $t$ 是不是 $s$ 的一个子串。 $\sum t\le 10^6$,$m\le 10^6$,时限 $1$ s。 判断一个字符串是不是 $s$ 的子串可以考虑这个字符串它是不是 $s$ 的任何一个位置开头的一段前缀,不过这里既然是在末尾,我们可以考虑倒着建字典树,然后把 $t$ 也反转一下就行了。 啥意思呢,我们可以举个例子,比如说 $abaab$,我们建出来长这样。 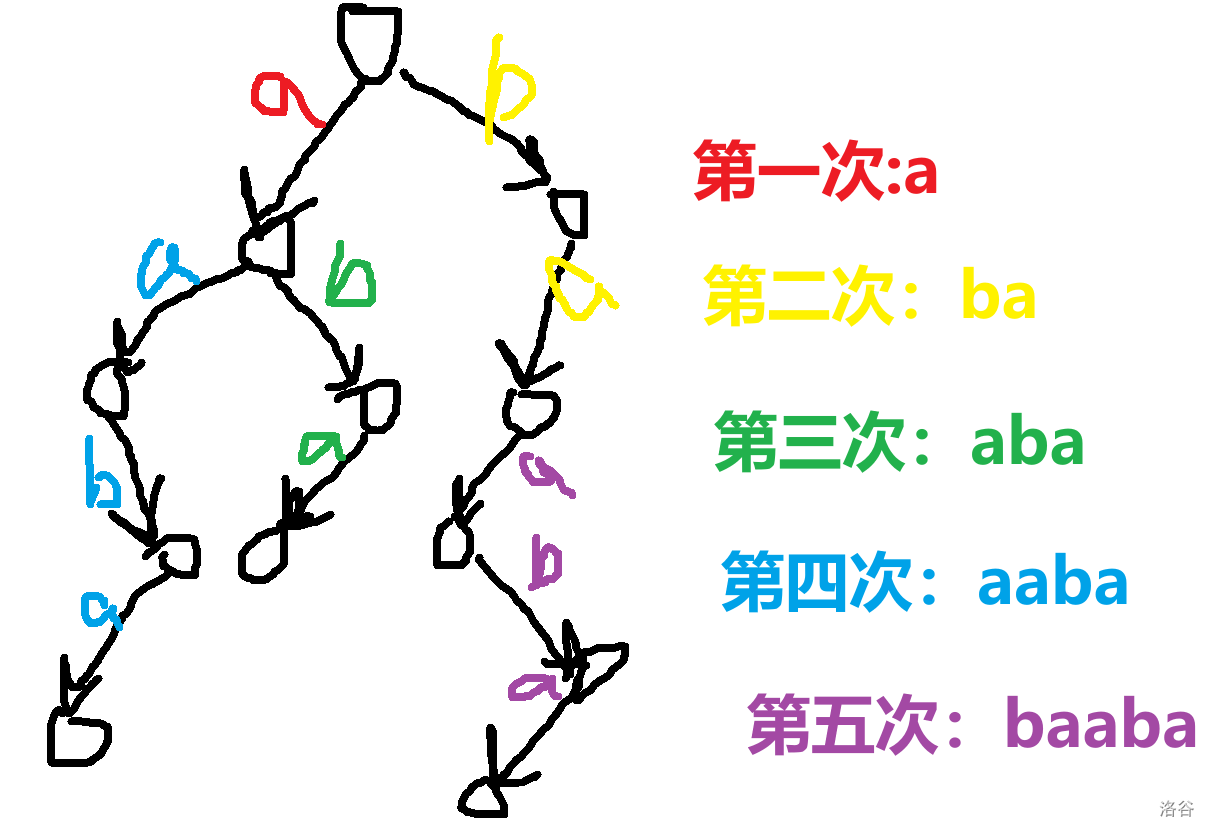 人话就是倒着建字典树,而这样做的好处是,在这题里每次在结尾加入一个字符,只需要在 trie 中加入一个字符串,于是这方便了我们建压缩 trie。 一个事实是这题 trie 中插入字符串的次数只有 $O(m)$ 次,所以压缩 trie 的节点只会有 $O(m)$ 个,虽然所谓的 $\sum s_i$,即插入的字符总数,有 $O(m^2)$ 个,但是不难发现对于压缩 trie 上的一条边可以用一对 $(l,r)$ 表示它是从 $s_r$ 到 $s_l$ 的一段字符串(因为是反过来的,所以是从右到左)。 所以通过这么做,我们得到了什么呢? 我们得到了一棵只有 $O(m)$ 个节点的字典树,它的每条边是 $s$ 的一段子串倒过来。 现在我们差的,只有快速建出这棵字典树了。 我们考虑加入一个新的后缀是什么样的。 接下来我们用 $S$ 表示新的后缀,需要注意 $S$ 是当前的 $s$ 倒过来。 它形如这样。 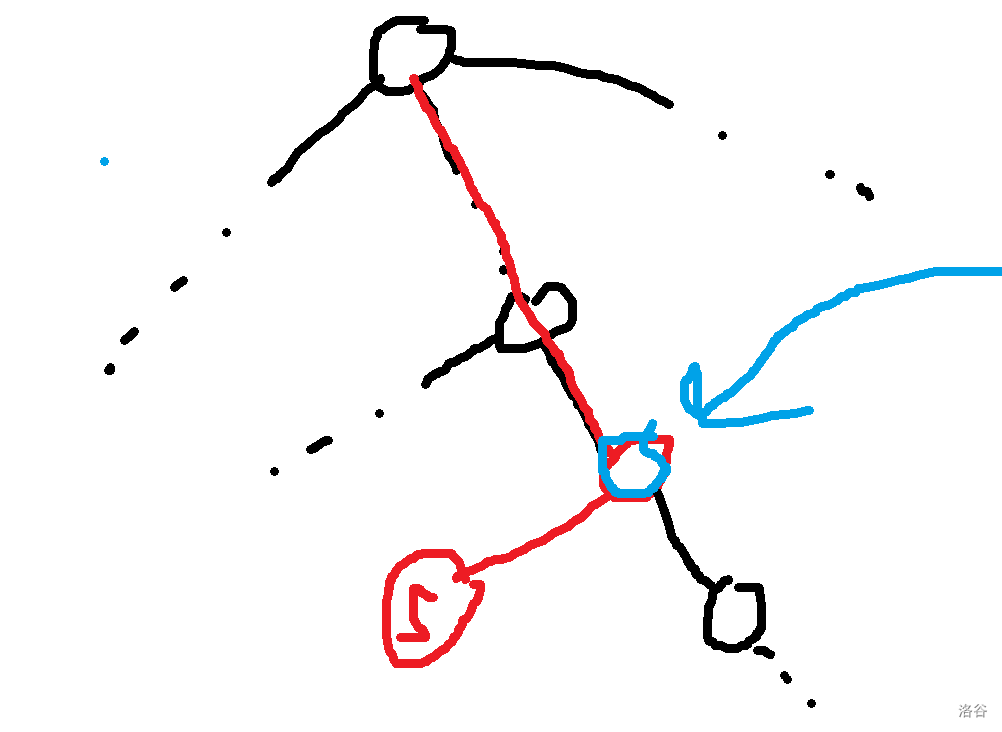 我们不难发现 $S$ 直接连向蓝色节点,所以只要考虑如何快速找出蓝色节点就行了。 设 $S'$ 是上一次插入的字符串,$S$ 是这次要插入的字符串。 我们可以考虑 $S'$ 和 $S$ 间的关系。 假设插入前字典树大概长这样。 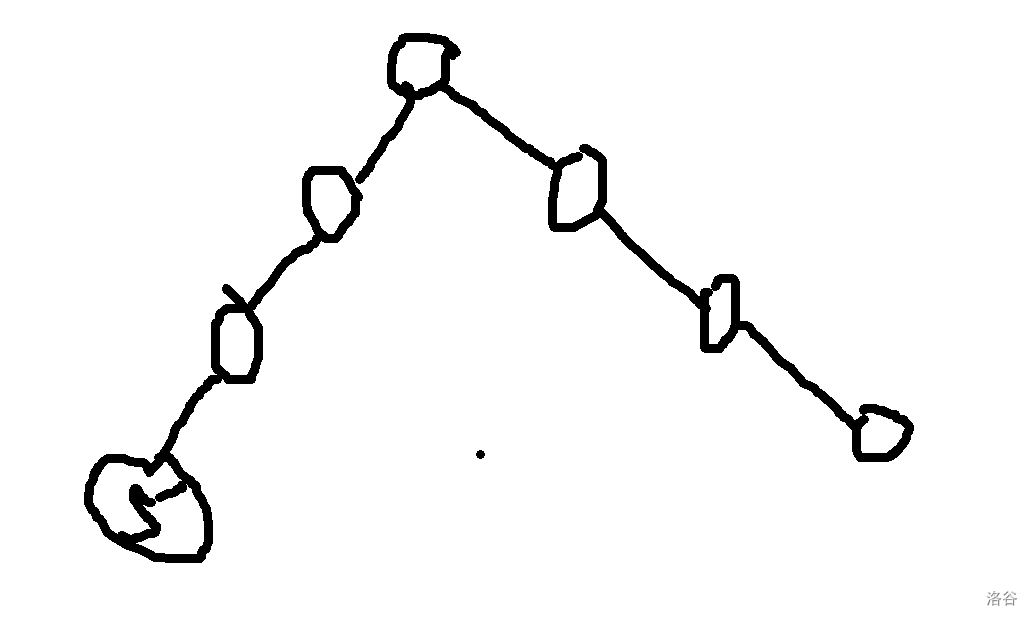 这里其实省略了很多节点,不过不太重要。 然后你要在蓝色节点插入 $S$。 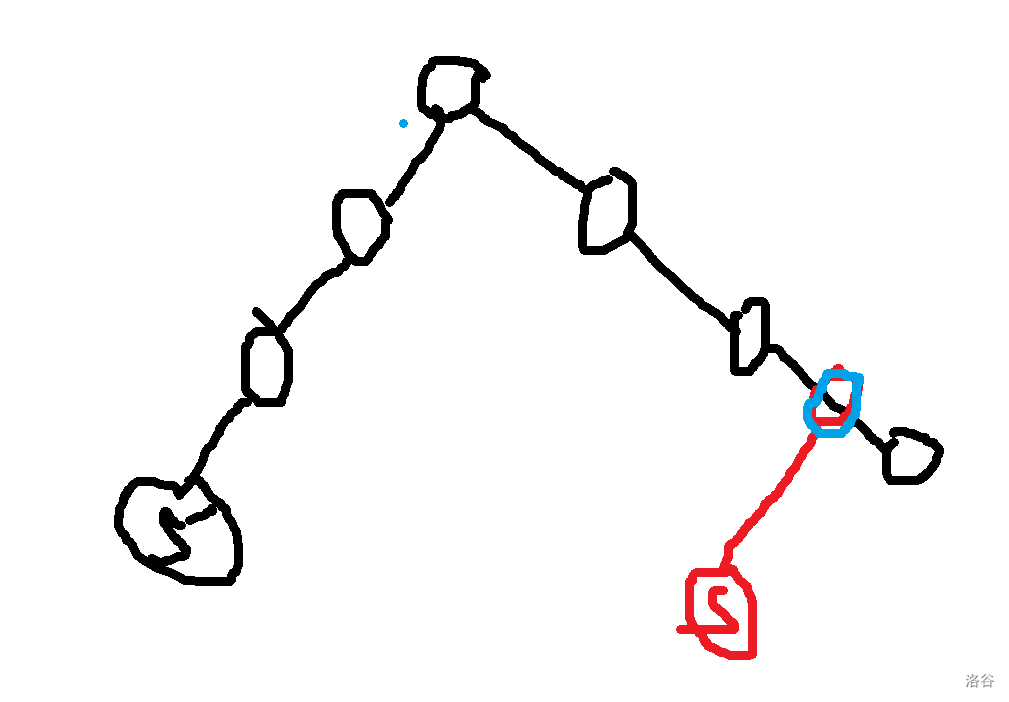 我们知道蓝色节点所对应的字符串一定在之前出现过。 假设蓝色节点所对于的字符串是 $T$。 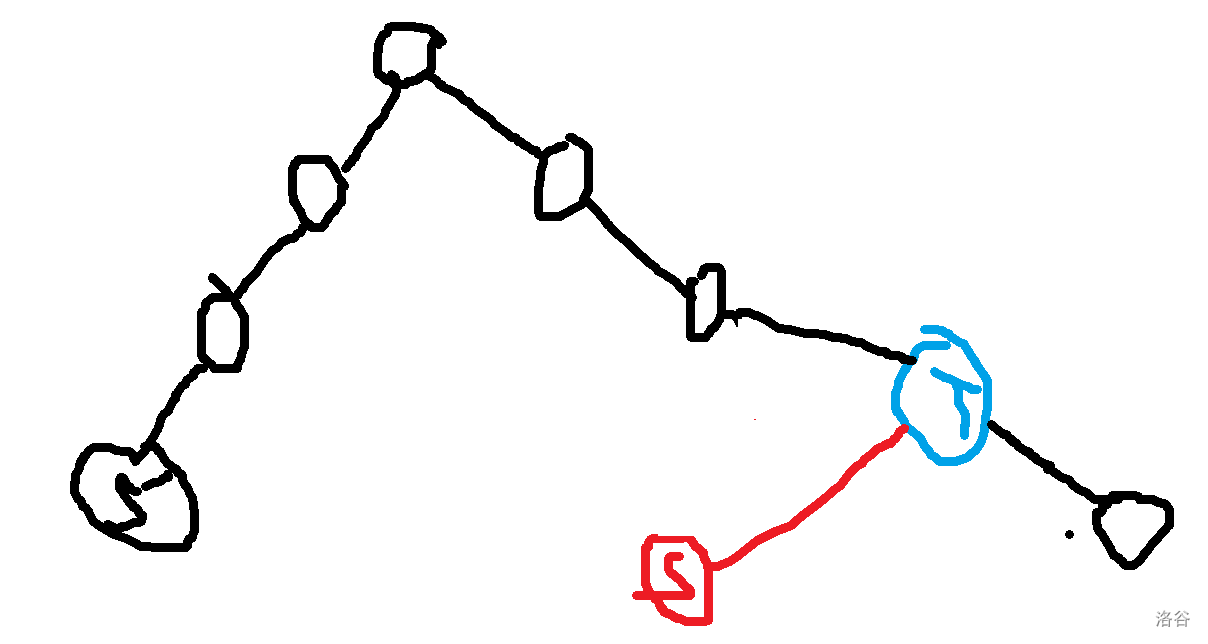 我们知道 $T$ 一定是以 $c$ 开头的,其中 $c$ 是一个字符,是 $S=c+S'$ 的 $c$。 令 $T=c+T'$。 因为 $T$ 是 $S$ 的一段前缀,所以 $T'$ 是 $S'$ 的一段前缀。 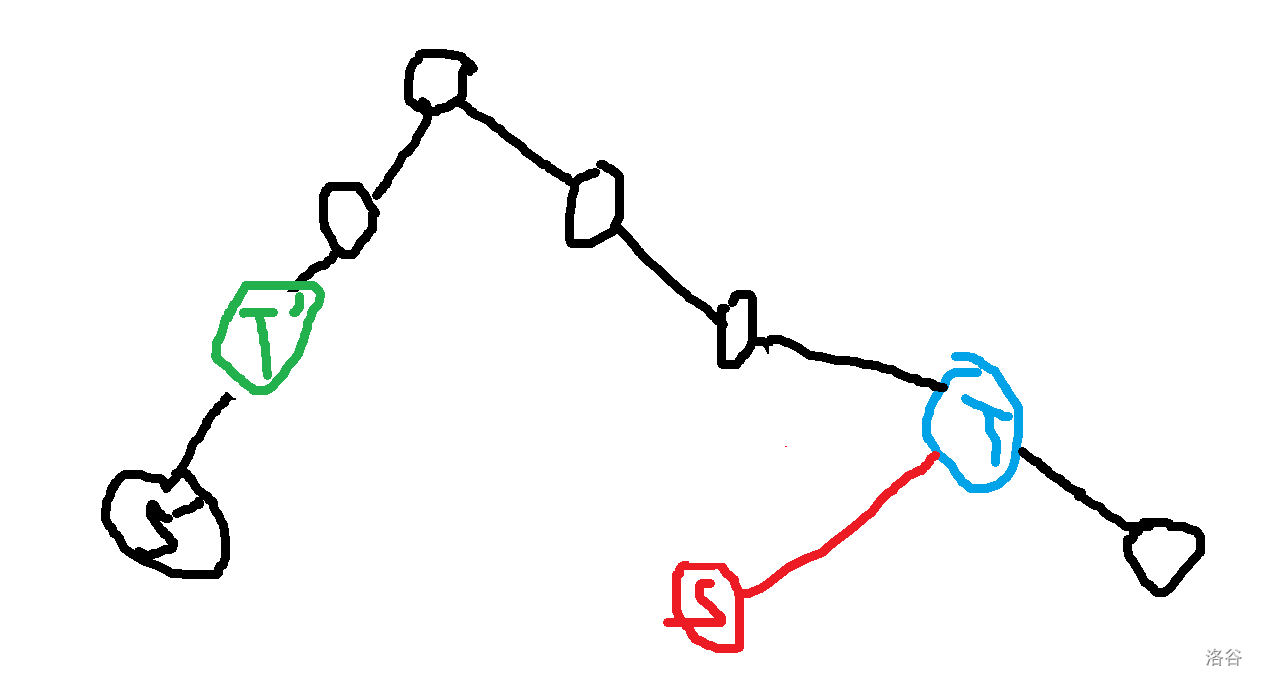 但是我们为什么要找到这个 $T'$ 呢? 因为这个 $T'$ 一定是 $S'$ 的祖先,并且找到了 $T'$ 后,只要我们通过某种方式对于一个节点,记录在它前面加一个字符 $c$ 会跳到哪个节点或哪条边上的节点,就可以从 $T'$ 跳到 $T$ 了。 并且我们稍加思索便能发现 $T'$ 一定是一个已经存在的节点,也就是,它不是在两个点的边中间的。 为什么呢? 然后我用了一个很冗长的证明(悲)。 ## 证明 我们首先要注意到很重要的一点是对于从原点向任意的 $c$ 走一条边,所构成的“子字典树”,把它“移”到原点,一定能被原树“覆盖”。 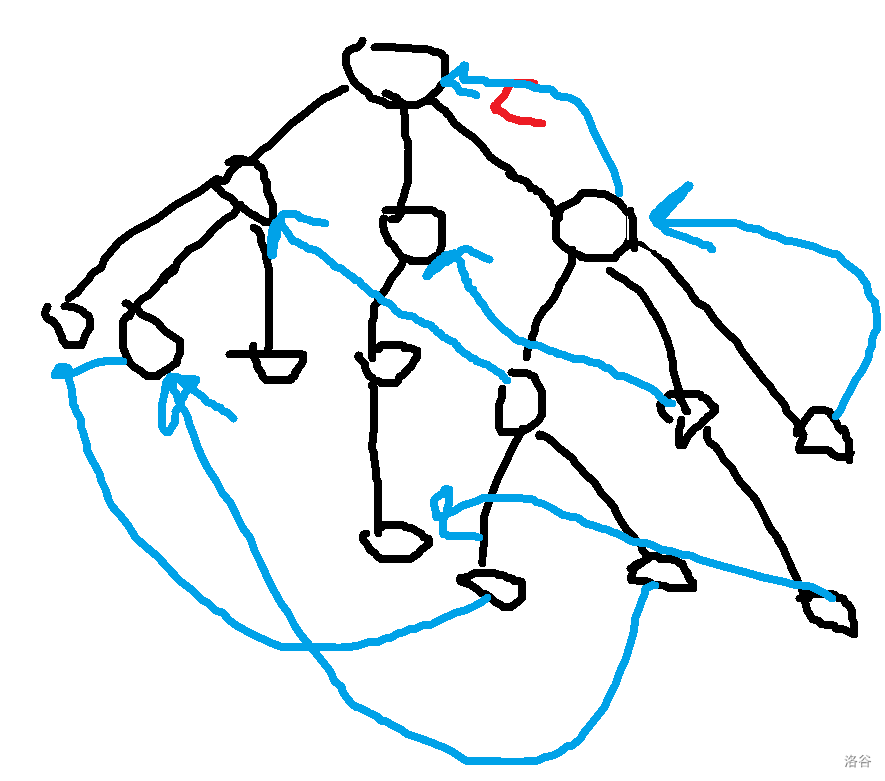 或者,换句话说,如果把字典树展开,那么每一个在 $c$ 边所对应的子树里的每一个节点,都对应 $S$ 的一个以 $c$ 开头的子串(注意 $S$ 是翻转后的 $s$),那么很显然把这个的第一个 $c$ 去掉也是 $S$ 的一个子串。 人话就是每一个 $c$ 子字典树内的节点都能对应到原字典树中的一个节点。 如果你上面都听懂了,那么对于压缩 trie,原点的节点相对于 $c$ 子树节点也是只多不少。 ~~当然如果你感性理解的话很显然~~。 反正就是,加完 $S$ 之后节点 $T$ 节点对应的 $T'$ 肯定是有的,所以加之前 $T'$ 肯定也有。 ## 跳过证明 如果一条边上的节点所对应的字符串前面可以加 $c$,而这条边后面的节点不可以加 $c$,感性理解,这是不可能的。 或者如果你看过别的后缀自动机的题解,用 endpos 来解释是很显然的,当然,我不太想写和别人一样的(?)。 暴力跳找 $T'$ 是不会有问题的,不过之后再说。 先想想对于一个节点,怎样通过某种方式,记录在它前面加一个字符 $c$ 会跳到哪个节点或哪条边上的节点。 我们不难想到,对于一条边上的节点,可以用它下面的节点找到。 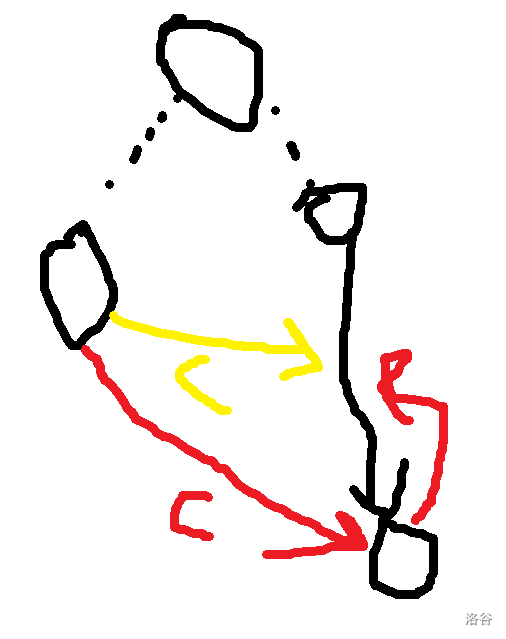 如果换个看法的话,你也可以认为是,一个节点对应的字符串包括了到它的那条边上的字符串。 设 $to_{u,c}$ 表示从第 $u$ 个节点对应的字符串前面加 $c$ 跳到的字符串。 假设现在已经找到了 $T'$,且之前的 $to$ 都被正确的处理出来了,现在我们考虑怎么维护这个 $to$。 假设目前的 $to$ 长这个样子。 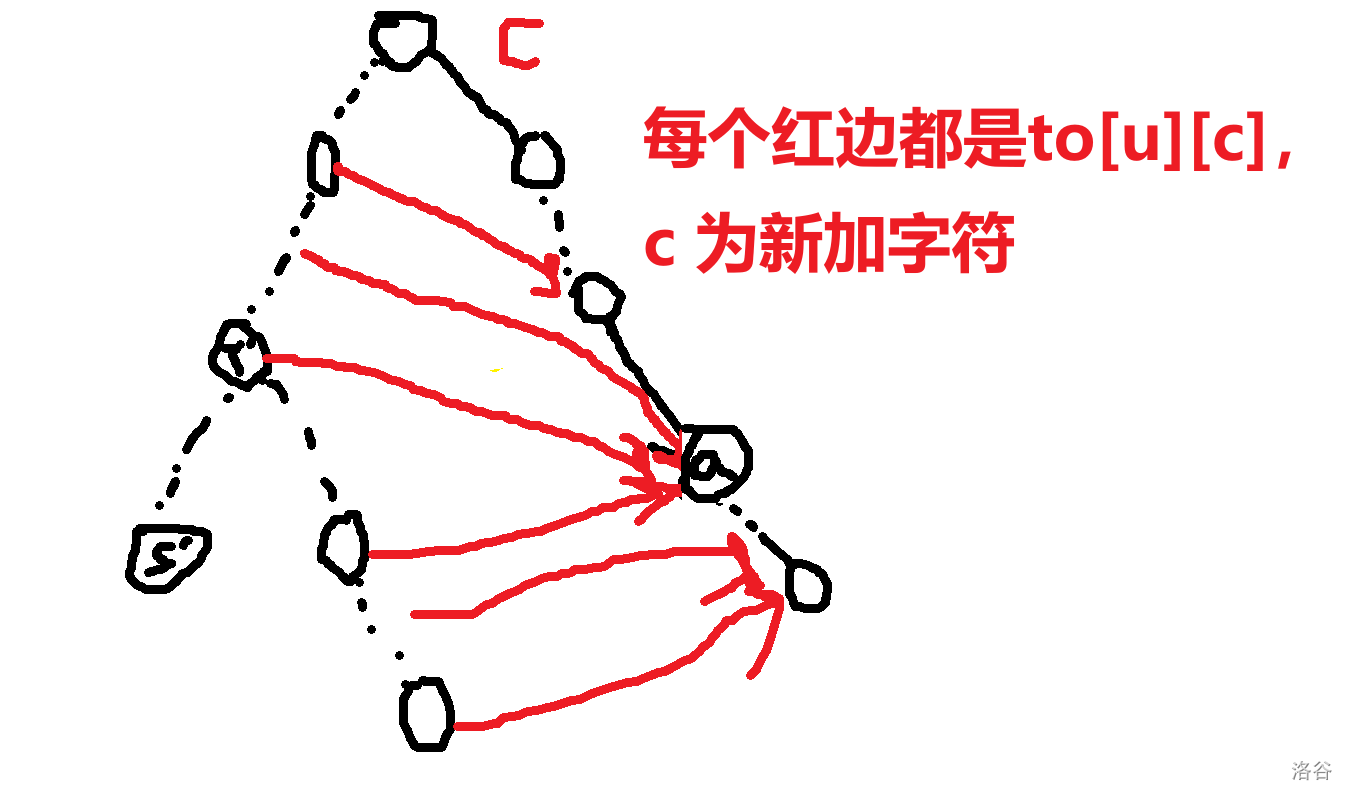 那些用虚线画的边可能有很多个点,实线画的边真的只是一条边。 很显然 $T$ 在 $a$ 和 $a$ 的父节点之间。 然后你把 $T$ 和 $S$ 插入,它应该会变成这样: 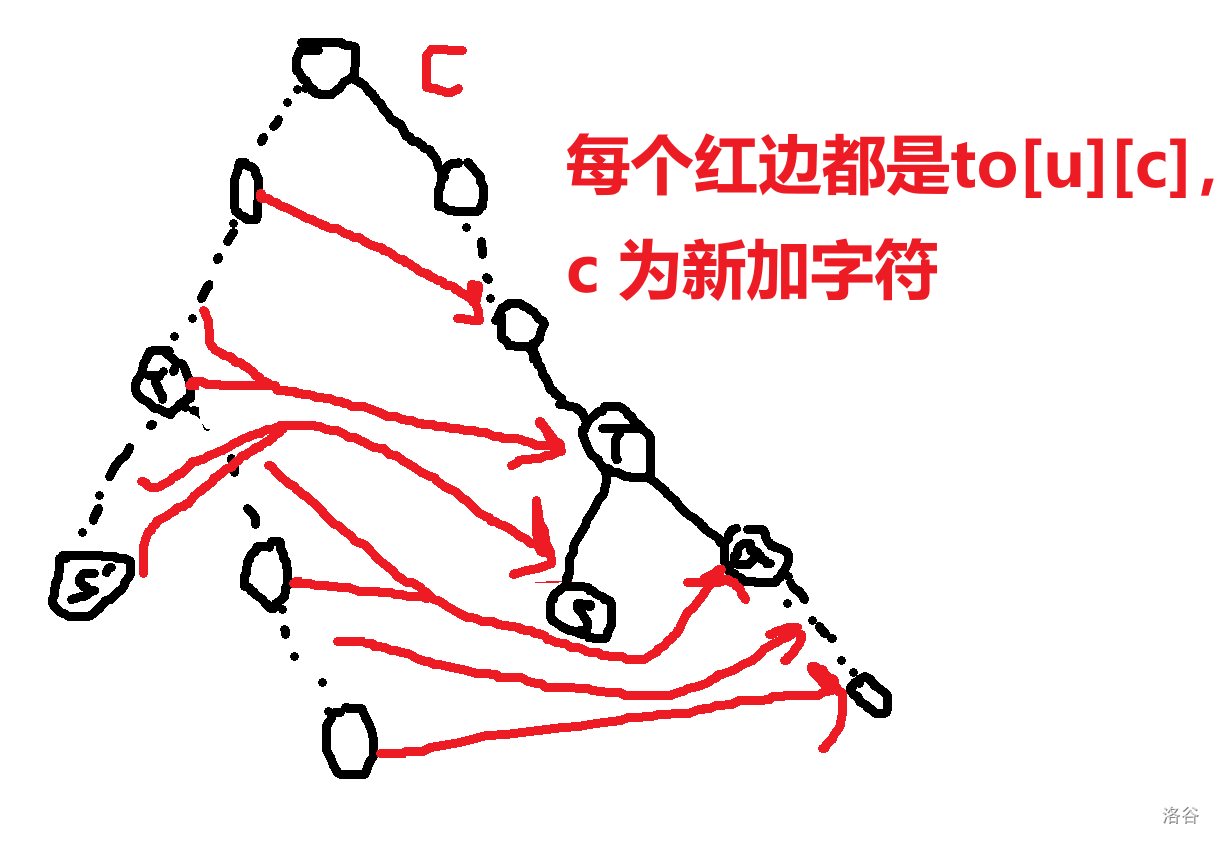 如果你问怎么找到 $T$ 啊?可以记录 $T'$ 等东西的对应的字符串长度,$T$ 的长度为 $T'$ 的长度加 $1$ 即可。 所以我们仔细看看上面怎么变化的,其实分为下面几个部分: $S'$ 到 $T'$ 前的 $to[u][c]$ 连到 $S$ 上。 $T'$ 到某个 $to$ 连到 $T$ 祖先的位置前的 $to$ 连到 $T$ 上。 其他剩下的都不变。 ~~于是我们用 LCT 维护 to 并跳链,做完了~~。 当然这里的比较特殊,如果均摊分析的话可以不用 LCT。 反正考虑压缩 trie 上你假设有个当前节点 $cur$ 到根之间的节点数为 $v$,$cur$ 初始是 $S'$。 跳 $T'$ 时,每跳一次 $cur$ 减 $1$。 从 $T'$ 沿着 $to$ 走的时候,$cur$ 至多加 $1$,因为前面说的 $c$ 子树的结构不会比原字典树更多,除此之外,最多还有一条从根到 $c$ 的边。 然后考虑暴力改从 $T'$ 到某个 $to$ 连到 $T$ 祖先的位置前的 $to$ 连到 $T$ 上,每改一次从 $T'$ 沿着 $to$ 走时 $cur$ 减 $1$。 然后从 $T$ 走到 $S$,$cur$ 加 $1$。 不管怎么说,这样就做完了。 如果你在 $s$ 上看的话(注意到是小 $s$),$to[u][c]$ 相当于在后面加一个字符 $c$ 会到的节点,而在压缩 trie 上向上跳相当于去掉一段后缀且这段后缀的 $to$ 相同,压缩 trie 上向下跳相当于加上一段以某个字符开头的后缀。 然后这就是大概流程,代码大概长这样,有几个边界条件没说,不过是简单的。 ```cpp struct SAM { int pa[2000005],to[2000005][26],l[2000005],d[2000005],cur=1,sl=1; int cnt[2000005]; inline void ins(char c) { c-='a'; int wz=++sl; cnt[wz]=1; d[wz]=0; l[wz]=l[cur]+1; while(cur!=1&&!to[cur][c])to[cur][c]=wz,cur=pa[cur]; int t=to[cur][c]; if(t) { if(l[t]!=l[cur]+1) { int t1=++sl; memcpy(to[t1],to[t],sizeof(to[t])); l[t1]=l[cur]+1; d[t1]=1; cnt[t1]=0; pa[t1]=pa[t]; pa[t]=t1; while(to[cur][c]==t)to[cur][c]=t1,cur=pa[cur]; t=t1; } d[t]++; pa[wz]=t; } else { to[cur][c]=wz; d[cur]++; pa[wz]=cur; } cur=wz; } } c; ```
正在渲染内容...
点赞
0
收藏
0