清北学堂 J to S Day-1

# 基本常识  
## 位运算相关  
### 左移右移  
$x << y = x \times 2 ^ y$  
$x >> y = x \div 2 ^ y$  
# 基本数据结构  
## 1.队列  
### 队列的手写  
………………  
### 单调队列
#### 定义  
一个队列单调递增或单调递减  
#### 实现  
##### 例题1：求区间和不大于M的最大区间长度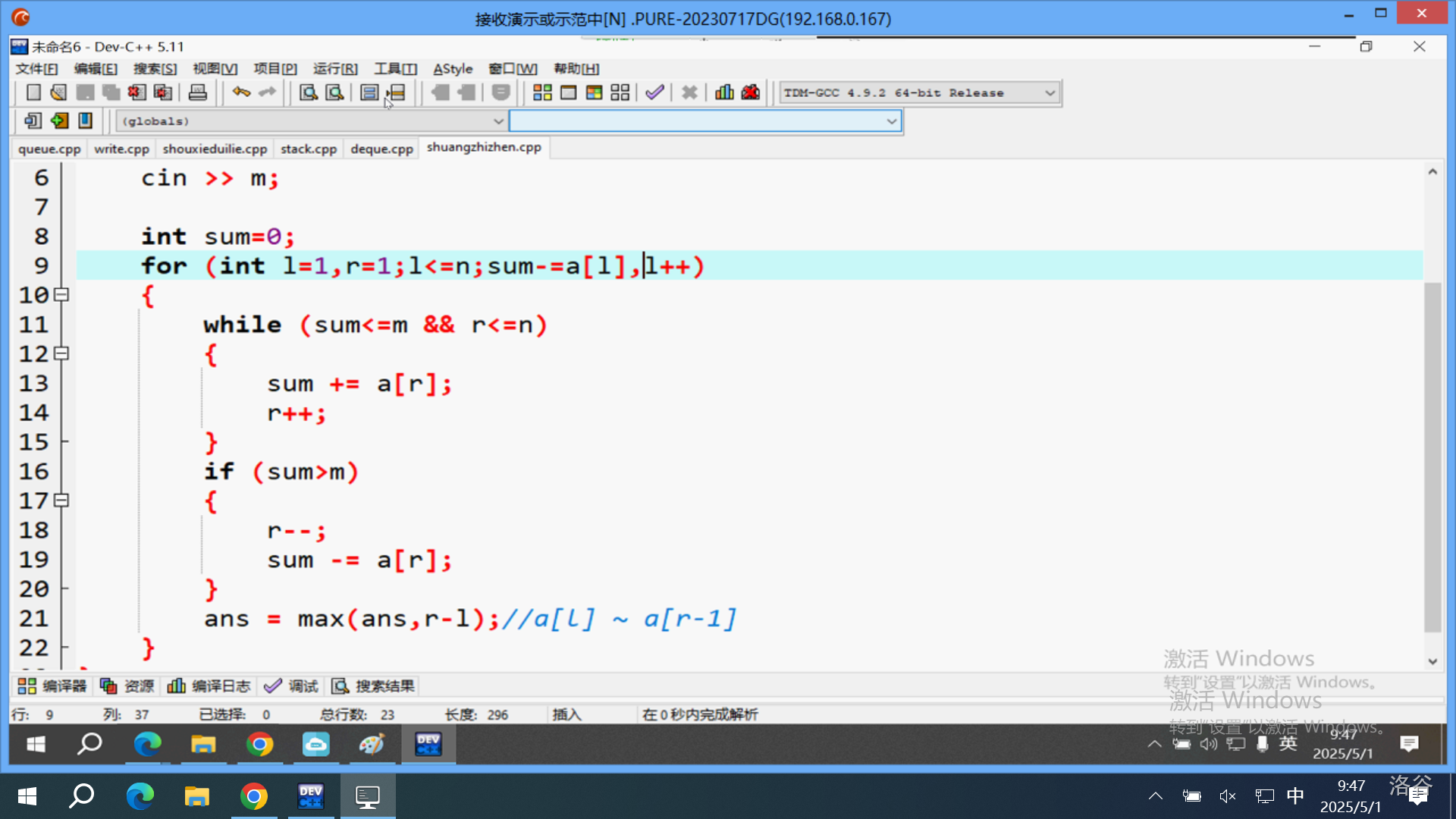  
![](https://cdn.luogu.com.cn/upload/image_hosting/vetztpob.png)  
#### 双倍经验：P1886 滑动区间 普及/提高-

## 2.栈  
………………
## 3.堆  
### 定义  
堆主要分为**小根堆**和**大根堆**。
小根堆的```top()```为该堆的最小值，大根堆则相反。
堆通过```priority_queue<&type>```实现。虽然**C++ STL**有实现小根堆的方法，但我们习惯用取相反数的方法构建小根堆，如：
```cpp
std::priority_queue<int> q;
q.push(i)   //大根堆
q.push(-i)  //小根堆
```
### 堆的常见操作  
#### 1. 重载小于号  
因为~C++发神经~我是蒟蒻，所以我不能直接将结构体放进堆中。我们需要对小于号进行重载。
##### 实现  
```cpp
struct rec{
  int a,b;
}
bool operator<(const rec &x,const rec &y){
  return x.a + x.b > y.a + y.b;
}
priority_queue<rec> q;
```
#### 2. 手写堆  
```cpp
struct heap{
	int a[1010];
	int n=0;
	
	int top(){
		return a[1];
	}
	void push(int x){
		n++,a[n]=x;
		int p=n;
		while(p!=1){
			if(a[p]>a[p/2]){
				std::swap(a[p],a[p>>1]);
				p=p>>1;
			}
			else break;
		}
	}
	void pop(){
		std::swap(a[1],a[n]),n--;
		int p=1;
		while((p<<1)<=n){
			int l=p<<1;
			int r=l|1;//p*2+1
			int pp=p;
			if(r<=n&&a[r]>a[l])pp=r;//pp=max(leftson,rightson)
			if(a[pp]>a[p]){
				std::swap(a[pp],a[p]);
				p=pp;
			}
			else break;
		}
	}
}; 
```
## 3. 并查集  
### 实现  
```cpp
int to[inf];
int go(int p){	//从P出发最后走到return
	if(p==to[p])return p;
	else {
		to[p] = go(to[p]);
		return to[p];
	}
} 
signed main(){
	std::cin>>n;
	for(int i=1;i<=n;i++)to[i]=i;
	//合并
	if(rand()%2) 
		to[go(p1)]=go(p2);
	else to[go(p2)]=go(p2);
	return 0;
}
```
## Trie树（字典树）  
![](https://cdn.luogu.com.cn/upload/image_hosting/8fuic9sz.png)
### 实现
```cpp
#include<bits/stdc++.h>
#define int long long
#define fir first
#define snd second
typedef std::pair<int,int> pii;

const int inf=1e9;

struct node{
	int nxt[2];	//nxt[0] nxt [1] 代表从当前点走0和1会到那里，如果那里是0则路径不存在
	node(){
		nxt[0]=nxt[1]=0;
	} 
}z[23333];
void insert(int x){	//向tire插入一个数 
	int p=root;
	for(int i=30;i>=0;i--){
		int y=(x>>i)&1;	//去除x二进制的地i位
		if(z[p].nxt[y]==0){
			cnt++;
			z[p].nxt[y]=cnt;
		} 
		p=z[p].nxt[y];
	}
}
int query(int x){	//从trie找一个数，是的它与x的异或值最大 
	int p=root,ans=0;
	for(int i=30;i>=0;i--){
		int y=(x>>i)&1;
		if(z[p].nxt[y^1]!=0)ans=ans|(1<<i),p=z[p].nxt[y^1];
		else p=z[p].nxt[y];
	} 
	return ans;
}
```
**tips:** 求最大值/最小值：Trie树  
求和：按位做  
## 杂七杂八的  
### 分块  
~线段树的盗版~  
$O(n\sqrt{n})$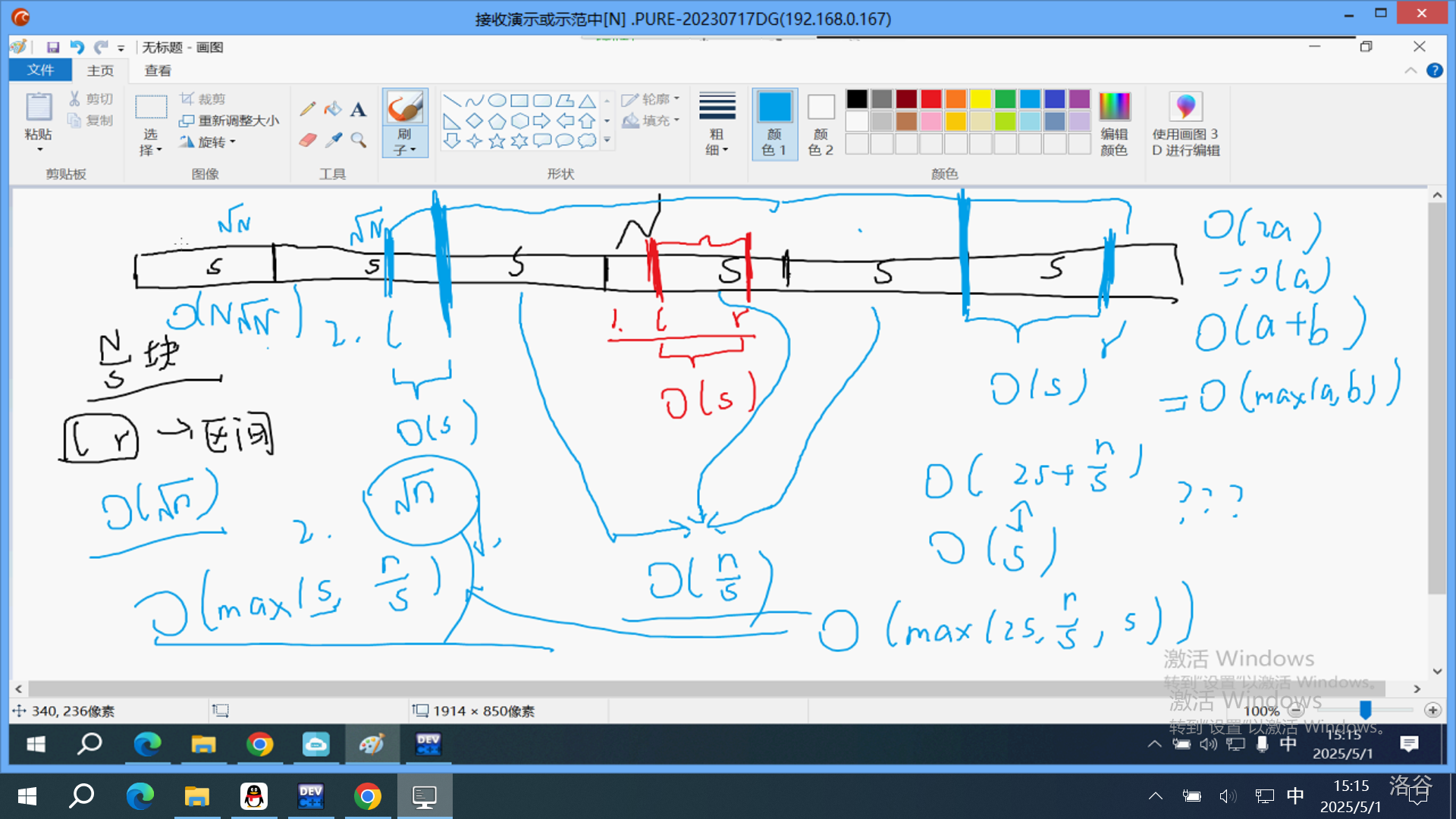  
![](https://cdn.luogu.com.cn/upload/image_hosting/tkvzli3p.png) 
#### 实现  
```cpp
#include<bits/stdc++.h>
#define fir first
#define snd second
typedef std::pair<int,int> pii;

const int inf=1e5;

int n,m;
int a[inf];
int belong[inf];	//第i个数属于第几块 
int sum[inf];	//第i块的和 
int daxiao[inf];
int col[inf];//代表第i块整体被加了多少 
int ans;

signed main(){
	std::cin>>n>>m;
	for(int i=1;i<=n;i++)std::cin>>a[i];
	int s=std::sqrt(n);	//每块的大小 
	for(int i=1;i<=n;i++){
		belong[i]=i/s+1;
		daxiao[belong[i]]++;
	}
	for(int i=1;i<=n;i++)sum[belong[i]]+=a[i];
	for(int x=1;x<=m;x++){
		int opt;
		std::cin>>opt;	//询问操作 
		if(opt==1){
			int l,r;
			std::cin>>l>>r;
			int ans=0;
			if(belong[l]==belong[r]){
				for(int i=l;i<=r;i++){
					ans+=a[i]+col[belong[i]];
				}
			}
				else{
					for(int i=l;belong[i]==belong[l];i++){
						ans+=a[i];
					} 
					for(int i=r;belong[i]==belong[r];i--){
						ans+=a[i];
					}
					for(int i=belong[l]+1;i<belong[r];i++){
						ans+=sum[i];
					}
				}
				std::cout<<ans<<'\n';
			}
		else{
			int l,r,v;
			std::cin>>l>>r>>v;
			if(belong[l]==belong[r]){
				for(int i=l;i<=r;i++)a[i]+=v;
			}
			else{
				for(int i=l;belong[i]==belong[l];i++)a[i]+=v;
				for(int i=r;belong[i]==belong[r];i--)ans+=a[i];
				for(int i=belong[l]+1;i<belong[r];i++){
					sum[i]+=v*daxiao[i];
					col[i]+=v;
				}
			}
		} 
	} 
	return 0;
}
```  
## 莫队  
### 定义：暴力！  
$O(n\sqrt{n})$  
```cpp
#include<bits/stdc++.h>
#define fir first
#define snd second
typedef std::pair<int,int> pii;

const int inf=1e5;
int n,m;
int cnt[inf]; 
int ans;
int a[inf];
int belong[inf];
struct query
{
	int l,r,id,ans;
}q[inf];
void ins(int x){
	cnt[x]++;
	if(cnt[x]%2==0)ans++;
	else if(cnt[x]!=1) ans--;
}
void del(int x){
	cnt[x]--;
	if(cnt[x]!=0){
		if(cnt[x]%2==0)ans++;
		else ans--;
	}
}
bool cmp1(const query &q1,const query &q2){
	if(belong[q1.l]!=belong[q2.l])return belong[q1.l]<belong[q2.l];
	else return q1.r<q2.r;
}
bool cmp2(const query &q1,const query &q2){
	return q1.id<q2.id;
}
signed main(){
	std::cin>>n>>m;
	for(int i=1;i<=n;i++)std::cin>>a[i];
	for(int i=1;i<=m;i++){
		std::cin>>q[i].l>>q[i].r;
		q[i].id	=i;
	}
	int s=std::sqrt(n);
	for(int i=1;i<=n;i++){
		belong[i]=i/s+1;
		
	}
	std::sort(q+1,q+m+1,cmp1);
	for(int i=q[1].l;i<=q[1].r;i++){
		ins(a[i]);
		q[1].ans=ans;
	}
	for(int i=2;i<=m;i++){
		int l1=q[i-1].l,r1=q[i-1].r;
		int l2=q[i].l,r2=q[i].r;
		if(l1<l2)for(int i=l1;i<l2;i++)del(a[i]);
		else for(int i=l2;i<l1;i++)ins(a[i]);
		if(r1<r2)for(int i=r1+1;i<=r2;i++)ins(a[i]);
		else for(int i=r2+1;i<=r1;i++)del(a[i]);
//		std::memset(cnt,0,sizeof(cnt));
//		ans=0;
//		for(int j=l;j<=r;j--){
//			ins(a[i]);
//		}
		q[i].ans=ans;
	}
	std::sort(q=1,q+n+1,cmp2);
	return 0;
}
```
## 逆序对-分治  
题面：给定 $n$ 个整数，求有多少个 $(i,j)$ ，使得 $i\lt j,a_i > a_j$  
### 实现  
```cpp
#include<bits/stdc++.h>
#define int long long
#define fir first
#define snd second
typedef std::pair<int,int> pii;

const int inf=1e9;

void merge(int l,int r){
	if(l==r)return;
	int m=(l+r)>>1;
	merge(l,m);
	merge(m+1,r);
	int p1=l,p2=m+1;
	for(int i=l;i<=r;i++){
		if(p1>m)b[i]=a[p2],p2++;
		else if(p2>r)b[i]=a[p1],p1++;
		else if(a[p1]<=a[p2])b[i]=a[p1],p1++;
		else b[i]=a[p2],p2++,ans+=m-p1+1;
	}
	for(int i=1;i<=r;i++){
		a[i]=b[i];
	}
}

signed main(){
	return 0;
}
```
**tips:** 分治用于 $1-N$ 的最大区间  
> # CCF的考纲是一个谎言
> # The CCF's list is a lie.