CF1443B Saving the City 题解 最后更新于 2025-05-01 18:18:05

[题目传送门](https://www.luogu.com.cn/problem/CF1443B) 本题是一道线性$dp$的入门题目。 $dp[i]$表示把前$i$个字符全部变为$0$所用的花费。 既然是$01$串，对于每个字符都有两种情况。 1.第$i$个字符是$0$，$dp[i]=dp[i-1]$。 2. 第$i$个字符是$1$，$j$是$i$前最后一个$1$的位置。如果$j<0$,$dp[i]=a$,否则$dp[i]=dp[j]+(i-j-1)*b$。 具体细节看下图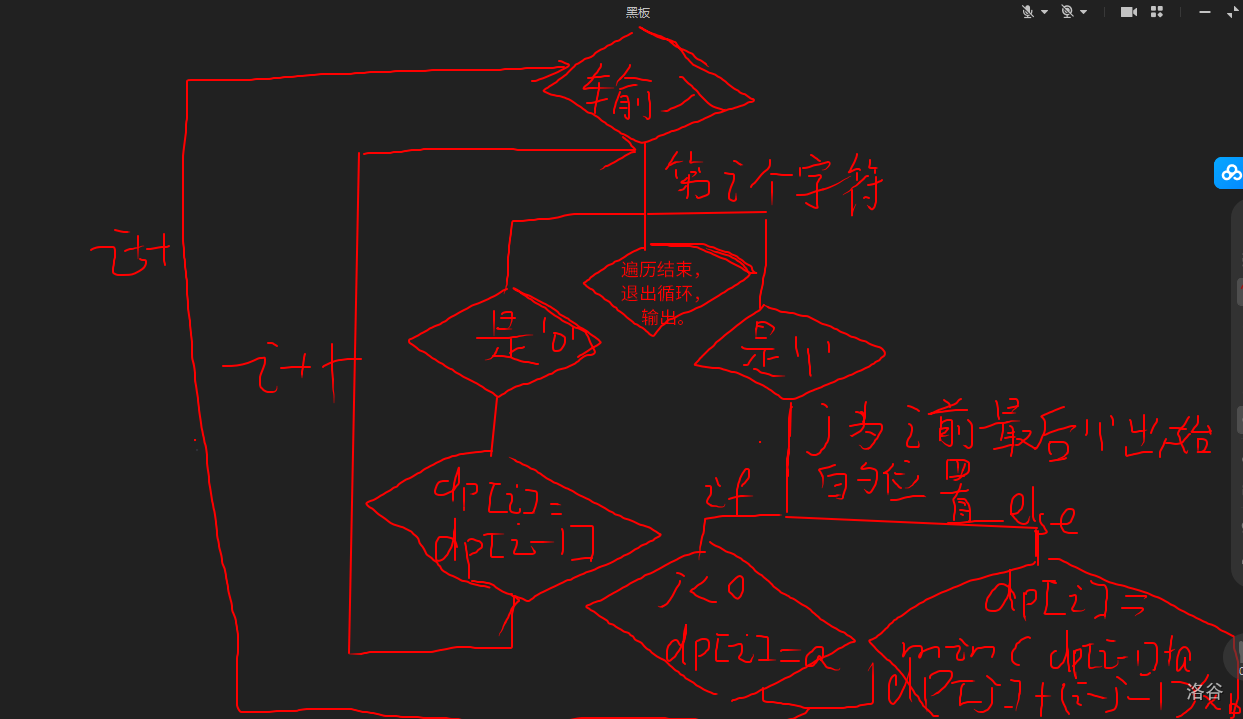：  code： ```cpp #include <bits/stdc++.h> using namespace std; int dp[100050];char ch[100005]; int main(){ int t; scanf("%d",&t); while(t--){ int a,b; memset(dp,0,sizeof(dp)); scanf("%d%d%s",&a,&b,ch); int n=strlen(ch); for(int i=0; i<n; i++){ if(ch[i]=='0'){ dp[i]=dp[i-1]; }else{ int j; for(j=i-1; j>=0; j--){ if(ch[j]=='1'){ break; } } if(j<0){ dp[i]=a; continue; } // if(ch[i-1]=='1'){ // dp[i]=dp[i-1]; // continue; // } dp[i]=min(dp[i-1]+a,dp[j]+(i-j-1)*b); } } printf("%d\n",dp[n-1]); } return 0; } ```