主页
搜索
最近更新
数据统计
申请密钥
批量保存
系统公告
1
/
1
请查看完所有公告
学习论
最后更新于 2025-07-20 17:53:41
作者
ltz761222
分类
个人记录
复制 Markdown
查看原文
删除文章
更新内容
- 2025.7.11——2025.7.12:重写。 - 2025.7.19——2025.7.19:增加胡同原理以及拓展胡同原理。 ## 引子 想一下,我们是怎么学习的?老师在台上讲,我们再下面记;老师发作业,我们就写;经常与老师互动。如果读者不介意的话,我将把这种学习方式叫做“封建学习模式”,今天在这里,笔者想要打开一道通往“资本主义学习模式”的道路。 ## 就我自己的经历 作为一个信息学奥赛的学生,我经常问自己:你是怎么做这个题目的?然后再把答案喂给计算机。可当题目的难度日益上升,比怎么做更重要的问题出现了——怎么思考。 而在长期的焦灼中,这种“对思考的思考”让我身心俱疲,我无法忍受这一切。我幻想自己是一个天才,扫一眼题目就知道答案,就像韦东奕一样;这种不现实的幻想又渐渐使我感到空虚,所以我幻想自己是黑马王者,经过长期的努力之后灵光乍现,一跃成为顶尖人物。从某种层面来讲,我更希望成为后者;或者说,我想要找到成为天才的路。这是很长的幻想与等待,就像坐在发烫的公交站座椅上一样——我无法用语言去形容一个人是怎么行尸走肉地思考的。人们也无法理解一个行尸走肉一般思考的人是怎么突然间开窍了,即使是发生在自己身上。 长期的思考过后,笔者已经开悟了,形成了自己的学习模式。因为当年走了很多弯路,所以著书修正这条道路。 --- ## 经验总述 ~~上述都是笔者的屁话,不必在意。~~ - 观点一:人与人最大的区别是思维方式。 - 观点二:人与人最大的差距是日常积累。 ### 观点一之论 想要追溯这一观点就要从古生物来讲起了。研究表明,当代人类的脑容量与智人(一种古人类,当代人类的祖先)并无本质差别,平均值也只是略高一些,不会影响智商。此时就有一个深刻的问题:智人、亦或者目之所及的所有飞鸟鱼虫,为什么单单只有当代人类拥有智慧?既然无以计年之前,智人就已经在此,那漫长的岁月中是什么导致山河万物没有发展智慧?其实答案早有指代。 如果按照国际标准将人类文明按照时间顺序绘制成**时间-文明指级**折线图,你会发现这是一条类指数曲线(指数曲线,一种前期增长缓慢,后期增长迅速的二维曲线)。也就是说无论任何年代,文明的发展依托于之前的发展。但之前的发展与新的发现并无直接联系,他们仅仅依靠树性(前者与后者存在依附关系)连接。按照《三体》所说,三体文明的发展就是平滑的折线,无论各个年代,都有着相近的发展速度。以我观之,此中奥秘在于思维方式。 如果你是原始人并发现了火,你会思考什么?用火烤的东西会变**好吃**,也会更加**安全**,火是很重要的**资源**。但是火并不能**长久保存**,这是很大的**弊端**。为了**钝化**这一弊端,我们需要长期保存火。而火的保存**因素**有**干燥的环境和足够的燃料**,这就是我们接下来需要做的。 看起来是一个简单的过程,实则不然。上段所有做标记的词语在原始人的认知中都是笼统的概念或者茫然。当然,有读者会觉得思考此问题不需要这么多过程。但正如人生下来就有肌肉却要报健身课一并得出样,难道全世界八十亿人没有了健身课就没有肌肉人吗?按照概率,会有的,但一定没有现在多。我们所标记的词语就相当于健身课。并不是健身课创造了肌肉人,而是那些训练出肌肉的人在长期的经验积累中创造了健身课。同理,古人类无法完全依托思考得出“篝火”,但是一些古人类却会歪打正着地“创造篝火”,并最终得出一样的结论。 可以说,思维方式让天才更加普通,智商与运气也无法主宰人生。同样的,一个优秀的思维方式可以拉开人与人的差别,拉马努金就是这样, ### 观点二之论 上阙我们已经论述了观点一,明确表示了思维方式的作用——成为后天的天才。但天才只是一种结实的皮囊。如果不往里面加以积累,充其量就是个空壳而已。笔者有一个小观点并未加在纲内,即**思维方式是一种抽象的概念,我们平时的思考描述是前者的必要体现**,恰巧用来论证此观点。可以说,积累知识实际上不仅是为了知识本身,更重要的是通过知识的生成过程亦或其他东西,可以吸收、运用别人的、常见的思维方式并转化成自己的思维方式。 举一个最古朴的例子,你能记住笔者写的上一句话吗?如果你能一字不差地复述下来,恭喜你,你走错路了。所谓的转化并不是等同于复述,而是有一天,你能开心地惊叫起来:“啊,原来是这么一回事!”之后再复述我刚刚说的话。这是一个神奇的过程,真正经历、理解的人很难描述清楚,没有经历过的人即使了解也无法感同身受。而同时,如果你真的经历了这一阶段,接下来最重要的是拼命学习,一直学,学到想吐为止。因为在那个时候,你的大脑皮层是唯一一次打开的,所有事情都能想清楚。如果你很幸运,之前就有很多知识储备,就应该全部回忆一遍,很有可能会像笔者这样开窍。 可以说,一个拥有海量知识的人就像滚烫的闭口板栗,给他一个榔头,就能迸发绚烂的花。也正因此,人与人最大的差别是日常积累。 ## 经验分述 ### 谈一些很泛泛的东西 如果给“文”,“理”各添加一个字组成词语,你会怎么选择? 笔者的答案是:“人文数理”。所谓“人文”,是一切以人为中心,为人所服务,或者有助于人进步的。任何的“文”,都会具有现实意义,其中联系千丝万缕,实则不可分割;所谓“数理”,即一切要有理论的数字依据,不能构建空中楼阁,且一脉相承,前后分明。 既然一切有迹可循,那便一定有章可奏。诸如高中数学,笔者来看所谓算式,不过“名,式,幂”三者结合罢了。又如初中政治,所谈不过“人的利益、人的精神、人的大小合集”而已,可分“主观个人与客观大小团体”来理解。当然,此等奥义非笔者一人可解,于此不再展开。 ### 谈一些仅仅是数理的东西 相比较“人文”,“数理”更需要思维方式的转变,即个人无法经常突破原有认知。与我而言,“数理”思维方式之广泛无可比拟。笔者总结主要内容,合为素养,其为: > 估范素养,具理素养,反列素养,多维素养,本质素养。 不分先后,没有大小,笔者接下来会详细分述。 #### 估范素养 估范,即估计范围;估范素养指遇见问题能估计其大致方向、内容、难度或其他方面的内容,也暗含猜想的意思。 估范素养很多时候只起到辅助作用,并不能直接解决问题。相反的,他通过预测,使得其余素养能够更快地发挥正作用,也具有简化冗杂步骤的作用。有时候,大胆的猜想会成为解决问题的关键。 #### 具理素养 具理,即具体和理论;具理素养指遇见具体问题能够转化成抽象理论,遇见过于抽象的理论可以赋予具体实践。例如学习组合数学时,有许多恒等式难以证明。但如果加以实际问题,将等式两侧转化成同一问题的不同方法,就可以很快证明;再比如一些问题拥有较高复杂度时,可以将一部分枚举转化成算式,通过预处理横向处理减轻纵向复杂度。 具理素养更像一门奇术,没用的时候一点用也没有,一旦有用就会是突破性的进展。 #### 反列素养 反列,反向和同列;反列素养指得到某一结论之后可以自行探索相反的结论和相似的结论。例如线段树(一种数据结构)中有求区间 $\max$ 的操作,读者在学会之后应该可以想到求区间 $\min$ 的操作。更深层次的,读者可以尝试求区间第 $k$ 大/小的操作。又如莫队(一种分块)可以离线求一维区间贡献,读者在学习后可以思考离线求二维矩阵贡献的方法。 反列素养还可以指将某一结论拓展,寻找之前学习中相近的结论,并加以融会贯通。当然,遇见问题的时候如果发现反过来做很快,可以考虑能否将反过来求出的答案再反过来。 反列素养可以帮助消化,加深印象,也是一种深刻的探索,有些情况下可以减少学习成本。 #### 多维素养 多维,多维度;多维素养一指遇见问题可以从不同方面思考;二指遇见问题可以将其按照不同层面剖分;三指遇见问题可以将较少的维度扩大,用长处填补短缺,也可以将过多的维度缩小,减少冗杂方案。你看,对多维素养的解释就是多维素养的实例。 多维素养中维度一般只有一维、二维、以及二维往上统称的多维。大多数情况下都是维度的转化、新增和减少。当然,如果笔者的眼界比较开阔,很多东西都可以套用维度,维度也不一定只有整数维。 多维素养适用范围很广,它的广度显然超越了数理,达到了文理贯通的标准。 #### 本质素养 本质,探求本质;本质素养指遇见任何事物都能自发探求深层原理,进而可以结合其余素养将复杂的问题简单化,冗多的问题整理化。 有概念的地方就有本质,本质与数理的全部内容息息相关。 ### 胡同原理(笔者自推) 这有一个老北京胡同群,其中被标记的是可以走的路。 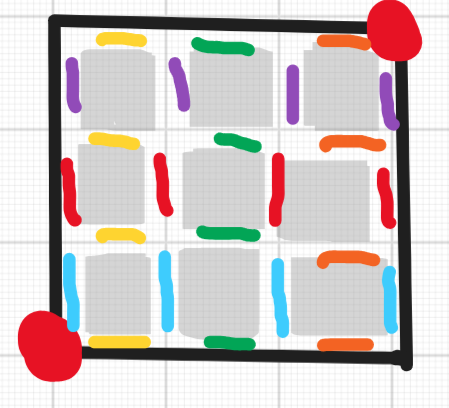 如果我们需要从左下角走到右上角,不难发现无论怎么走(假设不往回走),横着走的路径顺序一定是黄色、绿色、橙色。竖着走的路径顺序一定是蓝色、红色、紫色。这就是胡同原理的本质。 很明显,可以将不同颜色的路径赋予不同的意义,其中横、竖之间的意义没有关联,横、竖之内的意义具有链性关联。 举一个简单且便于理解的例子:我们称黄色、绿色、橙色、蓝色、红色、紫色分别代表买菜、洗菜、做菜、洗衣服、晾衣服、收衣服,我们在胡同中的每一种走法也就对应一种实际的做法。在不考虑能否真的会有神人按照这种路径生活的前提下,每一种路径的结果都是一样的:做好菜且洗干净了衣服。而显然,不同路径实现的难度、时间不一样。 胡同定理告诉我们,读者不应只考虑如何实现问题,更应该考虑的是具体实现中如何通过改变实现顺序更快地解决问题。 #### 拓展胡同原理 为了便于理解,我们拿出一个更小的老北京胡同。 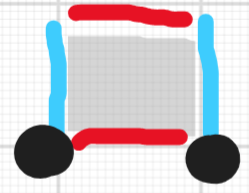 这时考虑往回走的情况。当我们需要从起点走到终点的时候,很明显,除了直接走到终点,我们还可以选择绕路。读到这里读者可能会有些许疑问,但需要理解的是,这里的胡同并不一定是现实中的胡同,有可能直接走的路很难走,甚至于不能走,反而绕一点远路会更好走。 举个简单例子。在 OI 中,如果我们需要用桶存储值域在 $-1000$ 到 $1000$ 之间的整数,较为普遍的想法是将整数 $x$ 存储在下标为 $x+1000$ 的桶中,在桶中查找的时候再将桶中的值减去 $1000$。该过程明显对应上图中的“远路”,但明显的,这种方法比直接傻傻存入要好得多。 拓展胡同原理告诉我们,当遇见无法解决、或者难以解决的问题时,我们可以考虑绕一些巧妙的远路,绕过原来的难点。
正在渲染内容...
点赞
0
收藏
0