[笔记] Tarjan 全家桶 - 洛谷保存站

# Tarjan 全家桶

## 算法概念

Tarjan 是一种基于**深度优先搜索（DFS）**的**线性算法**，用于求解**图的连通性**相关问题。

## 算法原理

Tarjan 基于 DFS 生成树，以下是几个重要概念：

顾名思义，DFS 生成树 就是在图上做 DFS 搜索，以搜索到的顺序为准将图转化为一棵树。

如图所示，原图的边被分为了四种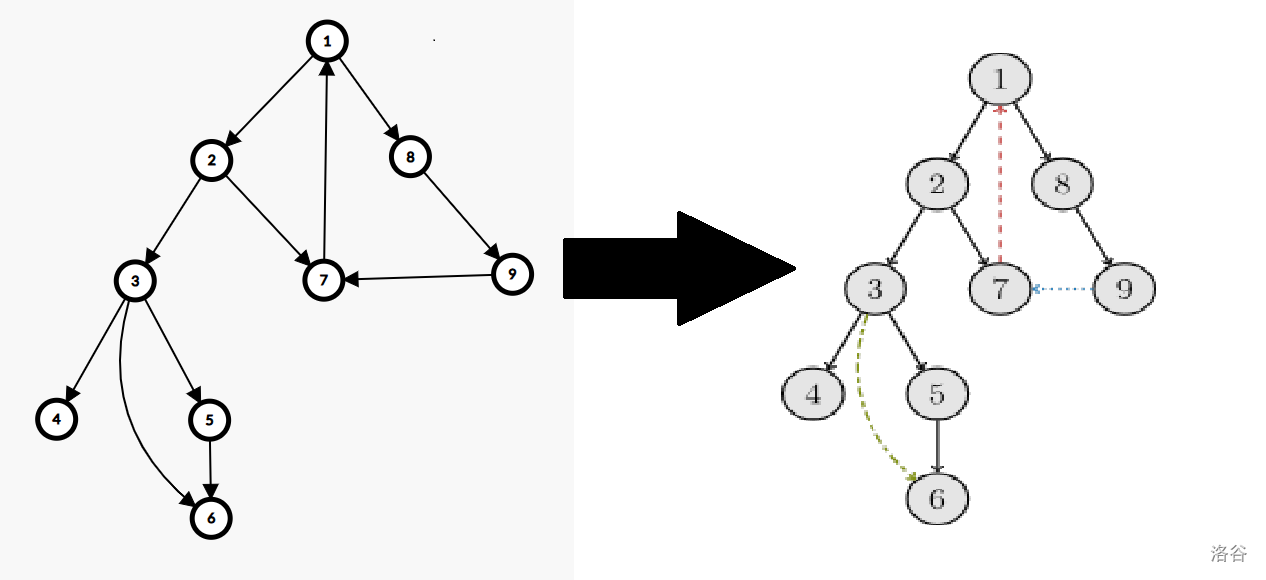：![](https://cdn.luogu.com.cn/upload/image_hosting/ho0c8bjx.png)

- **树边**：示意图中以**黑色边**表示，每次搜索找到一个**还没有访问过的结点**的时候就形成了一条树边。

- **反祖边**：示意图中以**红色边**表示（即 7 $\rightarrow$ 1），也被叫做**回边**，即**指向祖先结点**的边。

- **横叉边 (仅在有向图中出现)**：示意图中以**蓝色边**表示（即 9 $\rightarrow$ 7），它主要是在搜索的时候遇到了一个**已经访问过的结点**，但是这个结点**并不是**当前结点的祖先。

- **前向边**：示意图中以**绿色边**表示（即 3 $\rightarrow$ 6），它是在搜索的时候遇到**子树中的结点**的时候形成的。

其中在 Tarjan 算法中最重要的是**树边**和**返祖边**。

在 Tarjan 算法中最重要的是维护两个值：

- $dfn_u$: $u$ 节点是图中第 $dfn_u$ 个被搜索到的（dfs 序）;
- $low_u$：$u$ 节点通过若干条树边和**一条返祖边**可以去到的 $dfn$ 最小的节点。

## 算法实现

下面给出维护这两个值的代码，后面的所有应用都基于这段代码

```cpp
int dfn[N],low[N],tot;
void dfs(int u){
    dfn[u]=low[u]=++tot;
    for(int i=fir[u];i;i=e[i].nex){
        int v=e[i].v;
        if(!dfn[v]){
            dfs(v);
            low[u]=min(low[u],low[v]);//通过u子树中的某条返祖边来更新low
        }else low[u]=min(low[u],dfn[v]);//通过u的返祖边更新low
    }
}
```

## 强连通分量（SCC）

### 概念

强连通指的是在一张**有向图**中，**任意两个结点**连通。
而**强连通分量**是一个**极大**的**强连通子图**。注意这里的**极大**并不是指子图的**规模大小**很大，而是指这个子图要**尽可能大**。\
用**数学语言**来描述就是：

> 一个强连通子图 $G' = (V', E')$，\
> 其中 $V' \subseteq V$，$E' \subseteq E$。\
> $G'$ 极大，\
> 当且仅当不存在包含 $G'$ 的更大子图 $G'' = (V'', E'')$，满足 $V' \subseteq V'' \subseteq V$，$E' \subseteq E'' \subseteq E$。

### 算法原理

如果结点 $u$ 是某个**强连通分量**在**搜索树**中遇到的**第一个**结点，那么这个**强连通分量**的**其余结点**肯定是在**搜索树**中以 $u$ 为根的子树中。结点 $u$ 被称为这个强连通分量的**根**。

反证法：
假设有个结点 $v$ 在该强连通分量中但是不在以 $u$ 为根的子树中，那么 $u$ 到 $v$ 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 v 不在以 u 为根的子树中矛盾了。得证。

### 实现

我们用一个栈来实现，当某个节点 $u$ 第一次被搜索到的时候，将其入栈。当节点 $u$ 所有的边搜索完毕时出现 $dfn_u = low_u$，此时节点 $u$ 是一个强连通分量的根，与当前栈所有在 $u$ 上面的节点构成同一个强连通分量，记录后将 $u$ 和上面所有节点出栈。

### code

```cpp
int dfn[N],low[N],top,tot,belong[N],in[N],res;
/*
# belong[N] 记录每个节点属于哪个强连通分量

*/
int sta[N];
vector<int> scc[N];
void dfs(int u){
    dfn[u]=low[u]=++tot;
    sta[++top]=u;
    in[u]=1;
    for(int i=fir[u];i;i=e[i].nex){
        int v=e[i].v;
        if(!dfn[v]){
            dfs(v);
            low[u]=min(low[u],low[v]);
        }else if(in[v])low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        ++res;
        scc[res].push_back(u);
        while(sta[top]!=u){
            belong[sta[top]]=res;
            in[sta[top]]=0;
            scc[res].push_back(sta[top]);
            --top;
        }
        --top;
        in[u]=0;
        belong[u]=res;
    }
}
```
### 例题
#### [B3609 \[图论与代数结构 701\] 强连通分量](https://www.luogu.com.cn/problem/B3609)
## 割点

### 概念

> 对于一个**无向图**，如果把一个点**删除后**这个图的**极大连通分量数**增加了，那么这个点就是这个图的**割点**（又称割顶）。

通俗一点就是在原图中本来**连通**的两点在点 $u$ 删除后变得**不连通**了，那么点 $u$ 就是割点。

### 算法原理

那么怎么用 Tarjan 求割点呢？还是用到 $dfn_u$ 和 $low_u$ 两个值。

设节点 $u$ 的儿子节点为 $v$，当出现任意一个 $low_v \geq dfn_u$ 时，点 $u$ 为一个割点。

因为 $low_v \geq dfn_u$ 代表孩子无法通过任何一个返祖边去到子树外，那么该节点就和子树外的节点唯一路径是通过 $u$，如果 $u$ 被删掉了那么该节点就和子树外的节点不连通了，所以 $u$ 是一个割点。

此处有一个例外，设 $u$ 节点为根，若该点不是割点，则其他路径亦能到达全部结点，因此从根节点只「向下搜了一次」，即在搜索树内仅有一个子结点。如果在搜索树内有两个及以上的儿子，那么他一定是割点了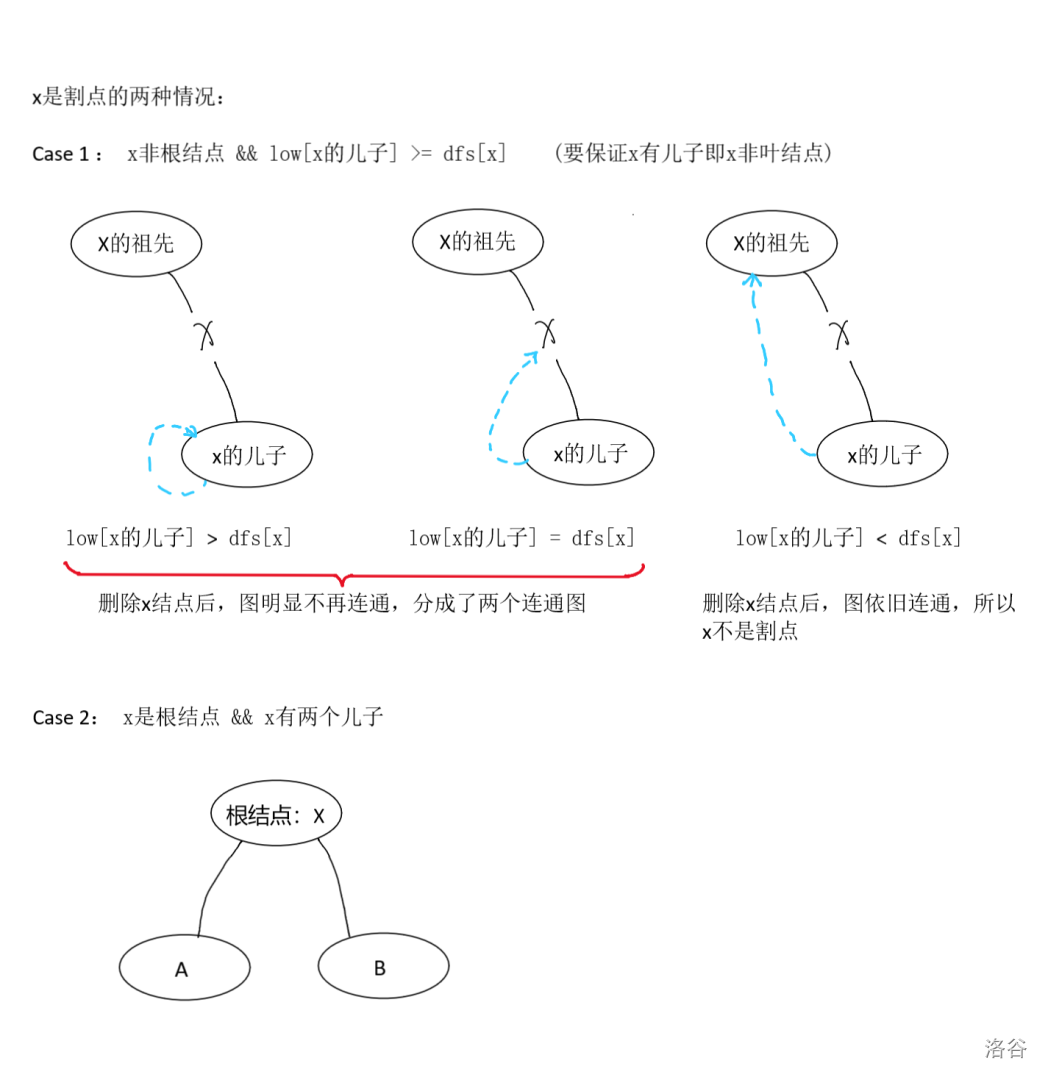

![](https://cdn.luogu.com.cn/upload/image_hosting/z6fd3qbk.png)

### code

```cpp
int cut[N];
int dfn[N],low[N],tot;
void dfs(int u,int root){
    int son=0;
    dfn[u]=low[u]=++tot;
    for(int i=fir[u];i;i=e[i].nex){
        int v=e[i].v;
        if(!dfn[v]){
            dfs(v,0);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&!root)cut[u]=1;
            if(root)++son;
        }else low[u]=min(low[u],dfn[v]);
    }
    if(root&&son>=2)cut[u]=1;
}
```

### 例题
#### [P3388【模板】割点（割顶）](https://www.luogu.com.cn/problem/P3388)
#### [P3469 \[POI2008\] BLO-Blockade](https://www.luogu.com.cn/problem/P3469)

## 点双连通分量（BCC）

### 概念

> 在一张连通的无向图中，对于两个点 $u$ 和 $v$，如果无论删去哪个点（只能删去一个，且不能删 $u$ 和 $v$ 自己）都不能使它们不连通，我们就说 $u$ 和 $v$ 点双连通。\
> 对于一个无向图中的 极大 点双连通的子图，我们称这个子图为一个 点双连通分量。

通俗的讲，点双连通分量就是在该子图 $G$ 内不存在割点，在该子图内删掉任意一个点，该子图仍然连通。

### 算法原理

首先需要了解一个性质：

- 对于一个点双连通分量，它在 DFS 搜索树中 $dfn$ 值最小的点一定是**割点**或者**树根**。

我们根据这个性质分类讨论

1. 当这个点为割点时，它一定是点双连通分量的根，因为一旦包含它的父节点，他仍然是割点。
2. 当这个点为树根时：\
   a. 有两个及以上子树，它是一个割点。\
   b. 只有一个子树，它是一个点双连通分量的根。\
   c. 它没有子树，视作一个点双。

我们用一个栈来维护，当满足 $dfn_u \leq low_v$ 那么节点 $u$ 与栈中节点 $v$ 上方所有节点构成一个点双连通分量。

### code

```cpp
int dfn[N],low[N],tot,top,res;
int sta[N];
vector<int> bcc[N];
void dfs(int u,int root){
    int son=0;
    dfn[u]=low[u]=++tot;
    sta[++top]=u;
    if(root&&!fir[u]){
        bcc[++res].push_back(u);
        return ;
    }
    for(int i=fir[u];i;i=e[i].nex){
        int v=e[i].v;
        if(!dfn[v]){
            dfs(v,0);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<=low[v]){
                res++;
                while(sta[top]!=v){
                    bcc[res].push_back(sta[top]);
                    --top;
                }
                bcc[res].push_back(sta[top]);
                --top;
                bcc[res].push_back(u);
            }
        }else low[u]=min(low[u],dfn[v]);
    }
}
```
### 性质
对于一个点双中的两点，它们之间简单路径的并集，恰好完全等于这个点双。

对于在同一个点双内的 $u,v,c$ 三点,一定存在一条通过从 $u$ 出发通过 $c$ 到达 $v$ 的简单路径。
### 例题
#### [P8435【模板】点双连通分量](https://www.luogu.com.cn/problem/P8435)
## 割边 (桥)

### 概念

> 对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。\
> 严谨来说，就是：假设有连通图 $G=\{V,E\}$，$e$ 是其中一条边（即 $e \in E$），如果 $G-e$ 是不连通的，则边 $e$ 是图 $G$ 的一条割边（桥）。

通俗的讲，本来连通的两点在删去一条边后变得不连通了，那么这条边就是一条割边（桥）。

### 算法原理

设节点 $u$ 的儿子节点为 $v$，当出现任意一个 $low_v < dfn_u$ 时，边 ($u,v$) 为一条割边。

其实跟割点差不多，原理不再赘述，而且不用考虑根节点的问题，~~至于为什么留给读者自行思考~~。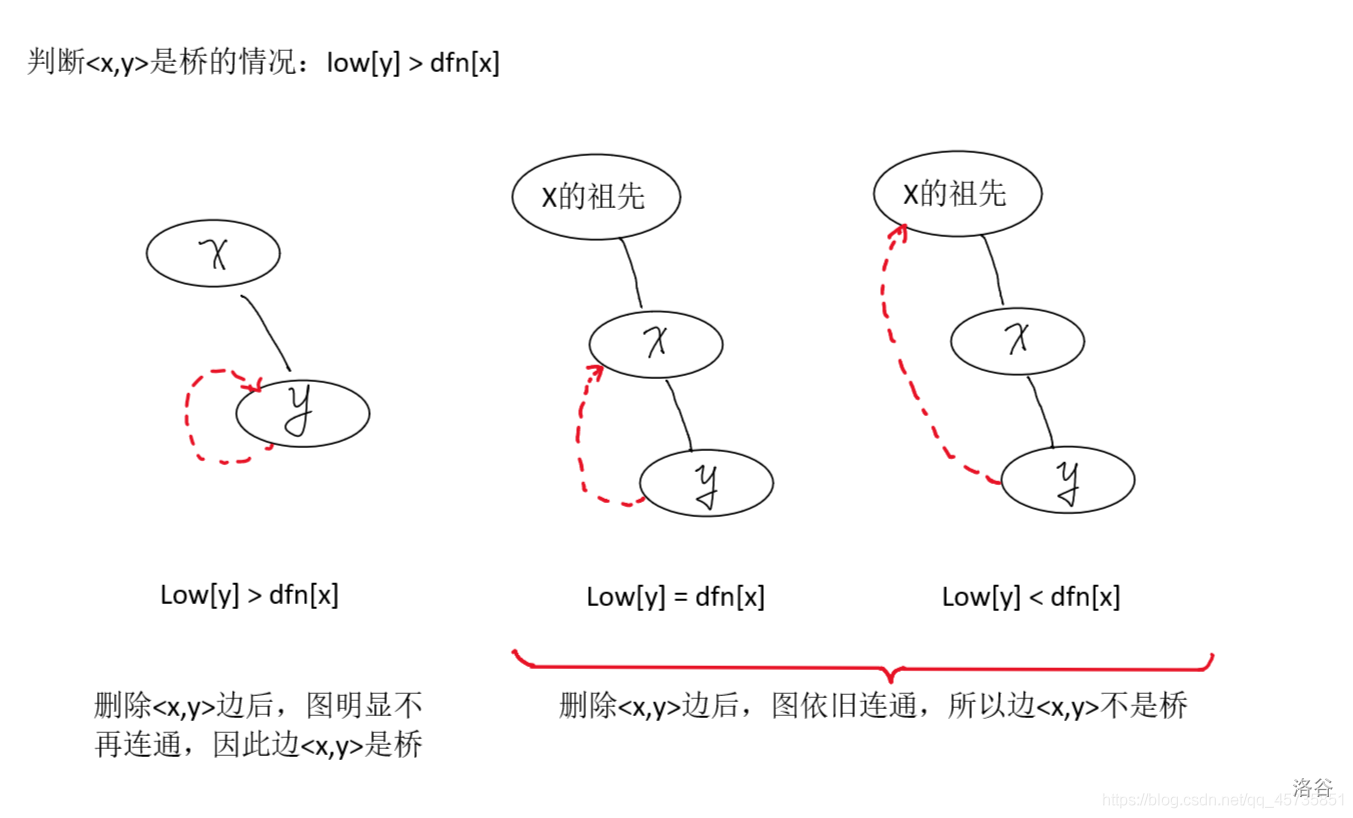![](https://cdn.luogu.com.cn/upload/image_hosting/m2pa24gp.png)

### code

```cpp
int n,m,dfn[N],low[N],cut[M],tot;
void dfs(int u,int in_E){
	dfn[u]=low[u]=++tot;
	for(int i=fir[u];i;i=e[i].nex){
		int v=e[i].v;
		if(!dfn[v]){
			dfs(v,i);
			if(dfn[u]<low[v])cut[i]=cut[i^1]=1;//双向边两条同时标记为割边
			low[u]=min(low[u],low[v]);
		}else if(i!=(in_E^1))low[u]=min(low[u],dfn[v]); 
	}
}
```
## 边双连通分量（DCC)

### 概念

> 在一张连通的无向图中，对于两个点 $u$ 和 $v$，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 $u$ 和 $v$ 边双连通。\
> 对于一个无向图中的 极大 边双连通的子图，我们称这个子图为一个 边双连通分量。

通俗的讲，边双连通分量就是在该子图 $G$ 内不存在割边，在该子图内删掉任意一条边，该子图仍然连通。

### 算法原理

边双连通分量比较简单，先求出所有割边，在将割边全部删去，剩下的每一个连通块都是一个边双连通分量

### code

```cpp
int n,m,dfn[N],low[N],cut[M],tot,res,belong[N];
vector<int> dcc[N];
void dfs(int u,int in_E){
	dfn[u]=low[u]=++tot;
	for(int i=fir[u];i;i=e[i].nex){
		int v=e[i].v;
		if(!dfn[v]){
			dfs(v,i);
			if(dfn[u]<low[v])cut[i]=cut[i^1]=1;//双向边两条同时标记为割边
			low[u]=min(low[u],low[v]);
		}else if(i!=(in_E^1))low[u]=min(low[u],dfn[v]); 
	}
}
void dfs2(int u){;
  belong[u]=res;
	Ans[res].push_back(u);
	for(int i=fir[u];i;i=e[i].nex){
		int v=e[i].v;
		if(belong[v]||b[i])continue;
		dfs2(v);
	}
}
```
### 例题
#### [P8436 【模板】边双连通分量](https://www.luogu.com.cn/problem/P8436)
## 缩点

### 概念

在一个图上将所有的 强连通分量 / 点双连通分量 / 边双连通分量 缩成一个点来处理，将整个图转化为一个 DAG / 树，然后再 搜索 / DP 。

### 例题

#### [P4306 \[JSOI2010\] 连通数](https://www.luogu.com.cn/problem/P4306)

#### [P4819 \[中山市选\] 杀人游戏](https://www.luogu.com.cn/problem/P4819)
#### [P8867 \[NOIP2022\] 建造军营](https://www.luogu.com.cn/problem/P8867)

## 圆方树

### 概念

树有很多很好的性质，并且便于用一些数据结构维护信息，圆方树是一种可以将一般无向图转化为树，并在树上使用一些树上技巧/数据结构来处理问题的算法。

其实圆方树最开始是处理一些仙人掌上问题的工具，后来经过一些修改使得可以在一般无向图上使用。

### 算法原理

先讲处理仙人掌的圆方树，将每个环建一个方点连接环上所有点，然后将这个环断开。

正在渲染内容...