Splay 和 LCT 最后更新于 2025-05-01 20:41:30

Splay 原本是平衡树，然后 LCT 借用过来做动态树问题。 ## Splay 不断旋转的平衡树。是一颗二叉搜索树，对于一般的平衡树查找方式均适用。 #### 辅助操作：dir操作 判断该节点的方向。 ```cpp inline bool dir(int x) { return ch[fa[x]][1]==x; } ``` ### 关键操作：rotate 和 splay。 rotate 和 splay 操作是重要的两个操作。 #### rotate 操作： 意义是将自己这个点旋上父亲。根据相对位置分为左旋和右旋。只需要维护旋转受到影响的四层的点即可。 以右旋为例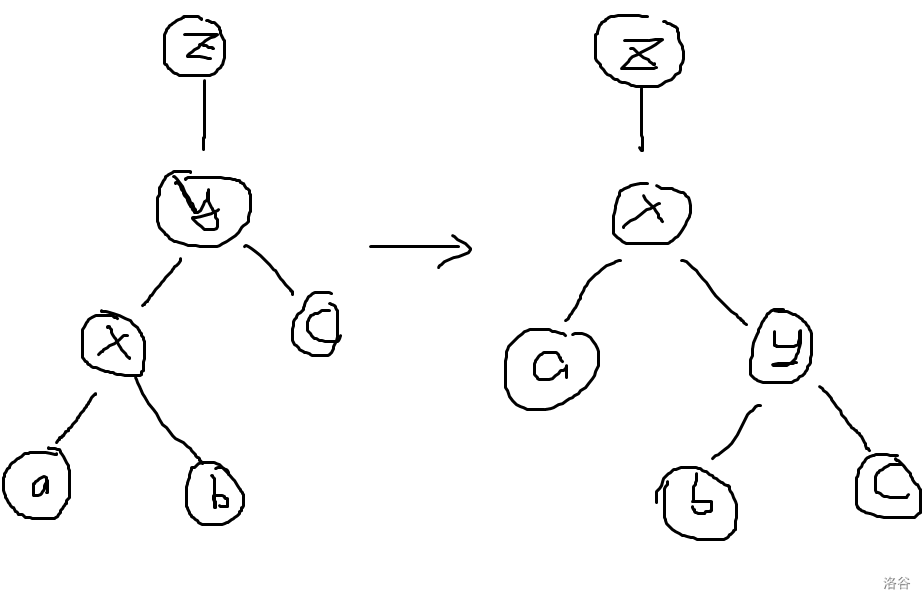：  如图，注意到 $x$ 到 $a$，$y$ 到 $c$ 这两条边是没有发生变化的。维护的是 $z,x,y,b$ 这一条链。 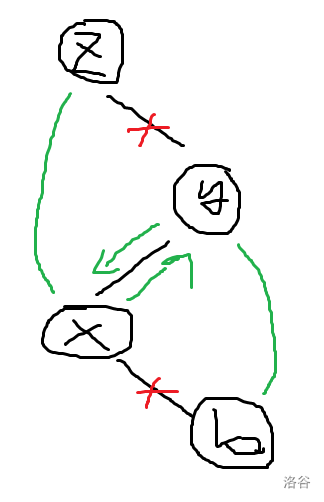 操作可以看作连两条跨越边，然后将中间这条边交换。 代码： ```cpp void rotate(int x)//将 x 节点 上旋到 父亲，将父亲 下旋到 儿子 { if(fa[x]==0) return ; int y=fa[x];int z=fa[y];int r=dir(x); //y 是 x 的父亲， z 是 y 的父亲 //分别维护四层：x 子节点，x，y，z //6 个变换操作加上 2 个 push_up 操作 if(ch[x][r^1]) fa[ch[x][r^1]]=y; ch[y][r]=ch[x][r^1]; if(z) ch[z][dir(y)]=x; ch[x][r^1]=y; fa[x]=z; fa[y]=x; push_up(y); push_up(x); } //在所有函数的实现时，都应注意不要修改节点 0 的信息。 ``` #### splay 操作 意义是将某一个结点 $z$ 作为根结点的子树中的结点 $x$ 翻到 $z$ 的位置上。理解为 $x$ 不断往上旋。 分为同向旋和异向旋。 同向旋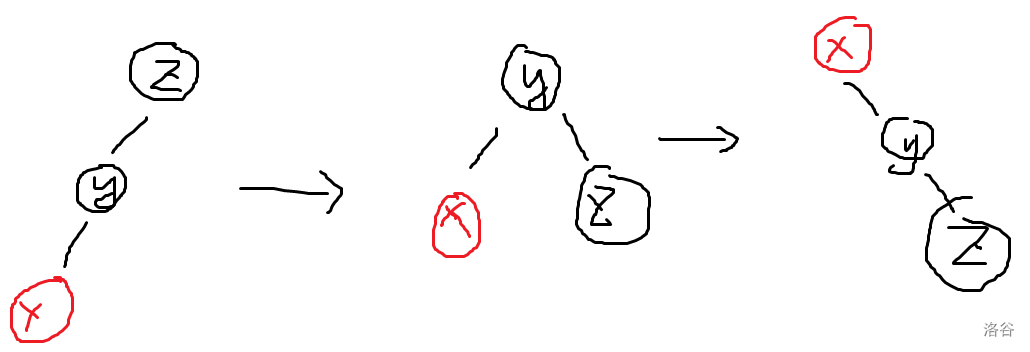：  异向旋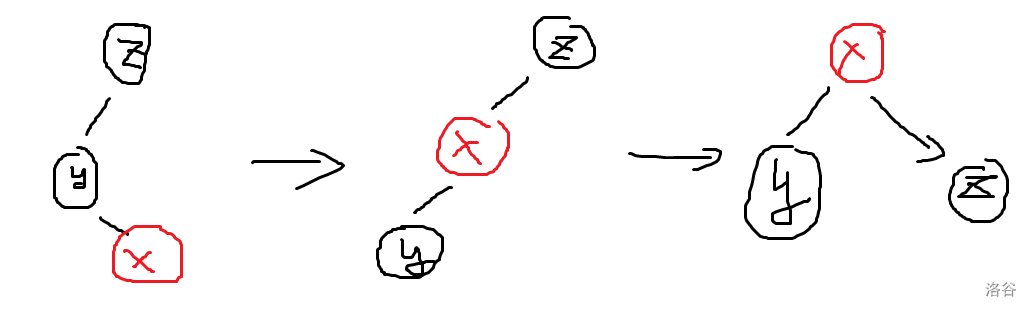：  怎么记忆？第一步旋靠中间的结点，第二步旋本结点。 总结：同向旋先旋父亲，再旋自己；异向两次都是旋自己。 代码： ```cpp //指定任意根节点 z，并将它的子树内任意节点 x 上移至 z 处： void splay(int& z,int x) { int w=fa[z];//我们希望判别是否到达其父亲，从而知道是否进行操作 for(int y;(y=fa[x])!=w;rotate(x))//y 作为 x 的父亲 { if(fa[y]!=w) rotate(dir(x)==dir(y)?y:x); //遵循法则：同向先 rotate 父亲，再 rotate 自己，否则 rotate 两次自己 //当父亲的父亲是 w 时，则说明父亲是 z ，rotate 一次即可 } //最后让根节点变为 x z=x; } ``` 以 [P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369) 为例讲其用法。 #### 预先查询函数： 1. `find` 函数：查询子树中是否出现 v（若没有则找前驱或后继），并将其旋上根结点。 2. `loc` 函数：按照排名访问，并将该位转移至根结点。 ```cpp void find(int& z,int v)//查询根中是否出现 v { int x=z;int y=fa[x];//y 记录最后一次 x 访问的点 while(x&&val[x]!=v)//不断向下遍历，直到找到非空或大于等于的节点 { y=x; x=ch[x][v>val[x]]; } splay(z,x?x:y); } void loc(int& z,int k)//按照排名访问，并将该位转移至根结点 { int x=z; while(x) { if(sz[ch[x][0]]>=k) { x=ch[x][0]; } else if(sz[ch[x][0]]+cnt[x]>=k) { break; } else { k-=sz[ch[x][0]]+cnt[x]; x=ch[x][1]; } } splay(z,x); } ``` #### 预先修改函数： `merge` 函数：合并两个结点，一般用于删除结点时。 ```cpp int merge(int x,int y) { if(x==0||y==0) return x+y; loc(y,1);//将y的最小点移到最上面（不是传 inf，传的是排名） ch[y][0]=x; fa[x]=y; push_up(y); return y; } ``` 具体看注释。 然后便可以实现平衡树的操作。**以下请注意：所有操作遍历的结点一定要进行伸展操作，并将其旋转到根上，在根进行操作**。 插入和删除： ```cpp void insert(int v) { int x=root,y=0; while(x&&val[x]!=v) { y=x; x=ch[x][v>val[x]]; } if(x)//存在结点 { ++cnt[x];++sz[x]; } else { x=++id; val[x]=v; cnt[x]=sz[x]=1; fa[x]=y; if(y) ch[y][v>val[y]]=x;//将边关系弄好 } splay(root,x); } bool remove(int v) { find(root,v); if(root==0||val[root]!=v)//找不到，或者里面根本没有点 { return false; } --cnt[root]; --sz[root]; if(cnt[root]==0)//该点已清空 { fa[ch[root][0]]=fa[ch[root][1]]=0; root=merge(ch[root][0],ch[root][1]); } return true; } ``` 值查排名，排名查值： ```cpp int find_kth(int k)//按照排名访问，返回值 { if(k>sz[root]) return -1; loc(root,k); return val[root]; } int find_rank(int v)//按照值访问，返回排名 { find(root,v); return sz[ch[root][0]]+(val[root]<v?cnt[root]:0)+1; //左子树，加上当前点，加上排名的 1 } ``` 查询前驱： 按照值 $v$ 访问节点（并上移至根部）； 如果根部的值小于 $v$，那么它必然是最大的那个，直接返回； 否则，在左子树中找到最大值，并上移至根部。 后继同理。 ```cpp int find_prev(int v) { find(root,v); if(root&&val[root]<v) return val[root]; int x=ch[root][0]; if(x==0) return -1; while(ch[x][1]) { x=ch[x][1]; } splay(root,x); return val[root]; } int find_next(int v) { find(root,v); if(root&&val[root]>v) return val[root]; int x=ch[root][1]; if(x==0) return -1; while(ch[x][0]) { x=ch[x][0]; } splay(root,x); return val[root]; } ``` 代码实现需要记住： 1. Splay 是一颗二叉搜索树，满足二叉搜索性质。我们需要用这棵树维护集合/序列信息。 2. 关键操作 rotate 和 splay 操作是为了确保时间复杂度正确。所以务必要实现。 3. 关于其他操作：找到的结点一定要进行伸展操作，并将其旋转到根上，在根进行操作。 4. 关于 push_up，请确保每次修改操作后都 push_up 信息。 ## LCT LCT 使用 Splay 进行实链剖分。 相当于将某个点的到根路径用一个 Splay 存储，形象理解为从下至上"打通"。 在原图中，每一条链都是一条自上而下的链，但是在辅助图中是用一个 Splay 存储。 辅助图中：分为虚边和实边。每一个 Splay 中恰好有一条边指向上层的 Splay，且辅助图中的虚边有： - 源结点对应的真实结点位于**当前 Splay 中最靠左侧的结点**。 - 指向结点指向的就是**真实结点**。 Splay 讲究认父不认子。一个点是当前 Splay 的根当且仅当它不是父亲的儿子结点。 ### LCT 中的 Splay 操作： ```cpp void rotate(int x) { int y=fa[x];int z=fa[y];int r=dir(x); if(!is_root(y))//改边要注意虚边父亲不应改儿子 ch[z][dir(y)]=x; ch[y][r]=ch[x][!r]; fa[ch[x][!r]]=y; ch[x][!r]=y; fa[x]=z; fa[y]=x; push_up(y); push_up(x); } // 从上到下一层一层 pushDown 即可 void update(int p) { if(!is_root(p)) update(fa[p]); push_down(p); } void splay(int x)//使 x 作为 Splay 树上的根 { //伸展时首先会将沿途修改的结点先进行 update update(x); for(int y;!is_root(x);rotate(x)) { y=fa[x]; if(!is_root(y)) { rotate(dir(x)==dir(y)?y:x); } } } ``` 注意事项： 1. 虚边父亲不应改儿子。 2. splay 时首先会将沿途修改的结点先进行 `update`（由上到下 `push_down`） ### 两个 LCT 的重要操作：`access` 和 `make_root`。 ```cpp int access(int x)//access 是将一条路径上的所有边弄成实边，其他成虚边 { int p=0;//p是上一个操作的结点 while(x) { splay(x); ch[x][1]=p; push_up(x); p=x; x=fa[x]; } return p;//这里 return p 是将最后一次的根 return 了，本质上是总根 //两个点分别 access，后者的返回值是两者的 LCA } void make_root(int x)//使指定的点成为原树的根 { x=access(x); // cout<<"mR:ac:"<<x<<'\n'; swap(ch[x][0],ch[x][1]); rev[x]^=1; //相当于将最右侧（最深）的点转移到最左侧（最上） } ``` `access` 操作图示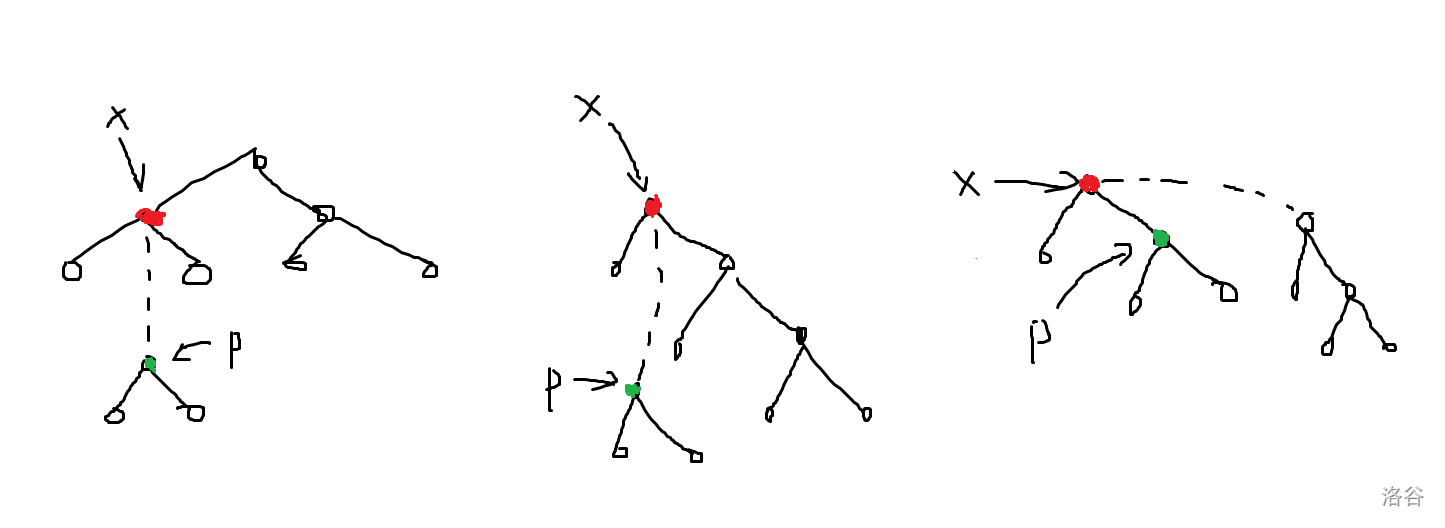：  `make_root` 操作图示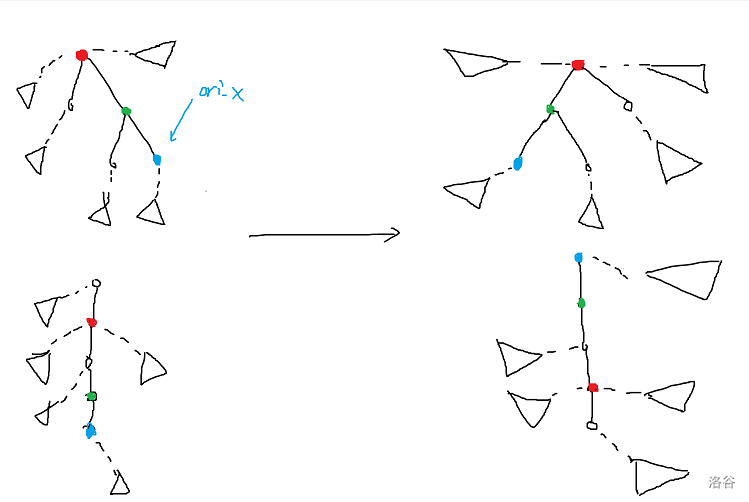：  `make_root` 相当于将最右侧（最深）的点转移到最左侧（最上）。 ### 动态树操作： ```cpp int find_root(int x)//查的是原树上的根 { access(x); splay(x); push_down(x); while(ch[x][0]) { x=ch[x][0]; push_down(x); } splay(x);//把 x 旋上去保证复杂度 return x; } bool link(int x,int y) { if(find_root(x)==find_root(y)) return false; if(x>y) swap(x,y); vis[make_pair(x,y)]=true; make_root(x); splay(x); fa[x]=y; return true; } //将其中一个作为根，指向 fa 为另一个即可 void split(int x,int y)//取出 splay 维护 x 到 y 的路径，并将 y 置为根。 { make_root(x); access(y); splay(y); } void cut(int x,int y) { if(x>y) swap(x,y); if(!vis[make_pair(x,y)]) return ; vis[make_pair(x,y)]=false; split(x,y); fa[x]=0; ch[y][0]=0; //这里是左儿子的原因是：split 操作中已经将 x 置为根， //然后再将 y 翻上去，故 x 深度一定比 y 小，去除左儿子 } ``` 代码复现后的注意事项： 1. `push_down` 只有非空儿子可以更新。 2. `splay` 要先从上到下 `update`。 3. `access` 要 `push_up`。 4. `find_root` 可以 `push_down`。 5. `cut` 后要 `push_up`。 6. `vis` 标记在 `link` 和 `cut` 函数要变为 `true` 和 `false`。 ## 例题 ### [P3703 [SDOI2017] 树点涂色](https://www.luogu.com.cn/problem/P3703) 静态树上用 LCT 的例题。 当我们改颜色时，我们将这一条链 `access` 一下，那么查询时答案就为**虚边**个数加 $1$。 动态维护每个时刻每个结点的权值。 考虑 `access` 操作对结点的影响。 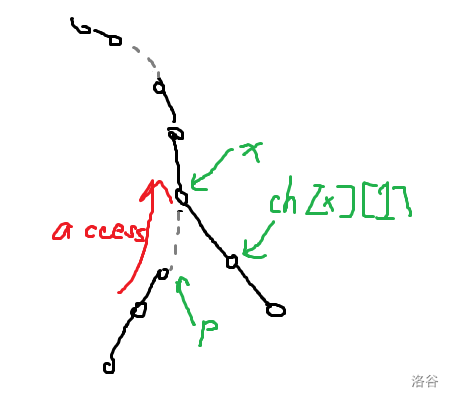 如图，在 $p$ 到 $x$ 这个过程，假设 $p$ 代表的真实结点的子树已经被修改好了。 令 $y$ 为 $x$ 结点的 Splay 的根结点。令 $v$ 为 $y$ 的权值。 修改时， - 首先需要将 $y$ 子树减去 $v-1$（原因是链祖先减去了 $v-1$ 种颜色）。 - $p$ 结点因为已经修改好了，所以再将 $p$ 代表的真实结点的子树加回 $v$。 - $x$ 的原右儿子 $ch[x][1]$ 由于原链被断开，所以 $ch[x][1]$ 代表的真实结点需要加上 $1$。 如果单独找 `find_root` 的话是不能 `splay` 的。所以现在需要快速求每个连通块的根。 树形态确定时的快速找 Splay 根的方法：**在原图上维护 DFS 序，然后每个连通块维护 DFS 序最小的结点，就是 Splay 上的根。** 不过也可以在搞一个 Splay 单独维护根。 ### [CF1039E Summer Oenothera Exhibition](https://www.luogu.com.cn/problem/CF1039E) 最难写。 首先当 $k$ 不变时，显然可以贪心往后取。将每个点与后继点连边之后，形成一个内向树。答案就是 $1$ 号点到 $n+1$ 号点的点数量减 $1$。 注意到：跳的次数越多，每一条距离越小；反之，每一条距离越多，跳的次数越少。即**跳的次数和跳的距离呈反比**。考虑平衡规划。 设平衡阈值为 $B$。 对于大于 $B$ 的一跳，我们可以直接二分 + ST 表维护，显然跳跃的次数是 $O(\frac {n^2} B)$。 对于小于等于 $B$ 的一跳，我们用LCT 维护。**因为每个点小于等于 $B$ 的跳只有 $O(B)$ 个，所以 LCT 加边删边的次数只有 $O(nB)$ 次**。 所以每个点向后 $B$ 个点维护其加边的时间（即极差），然后离线询问，在每次询问之前将 LCT 重构一遍即可。 #### 实现时需要注意的问题和犯过的错误： **LCT 跳跃：** LCT 显然会形成一个森林。可以用标记 + `access` 操作来知道到根的长度，但是 `link` 和 `cut` 操作或是其他什么操作会导致根发生改变，使得 `access` 操作指向一个非根。如何优雅地构建 `link` 和 `cut` 函数？ 首先删边加边一定是合法的，所以不需要特判。 加边时，假设是 $x$ 指向 $y$，那么 $x$ 一定是其 LCT 树上最上端的 Splay 的最左侧点（就是 $x$ 是根），所以直接将 $x$ `splay` 上去（或者 `access`），然后将其父亲改为 $y$ 即可。 删边时，假设是 $x$ 指向 $y$，那么将 $y$ 打通后（`access`），$y$ 的一个虚儿子所代表的子树一定是 $x$ 所代表的子树。将 $x$ 旋上去，那么 $x$ 的父亲必然是 $y$，让 $x$ 的父亲变为 $0$ 即可。 **$k$ 路归并：** 显然排序 $O(nB)$ 个数据复杂度太高了，然后发现每个点的向后 $B$ 个数据是已经排好序的，所以上个 $k$ 路归并。 **$\text{lg2}$ 数组** 这个东西能写错？写代码时写成 `lg2[i]=lg2[i-1]+((1<<(lg2[i]+1))==i);`。发现什么问题吗？是 `lg2[i-1]` 不是 `lg2[i]`。**所以以后数组和数据结构一类的东西要测正确性才行。** ### [P4219 [BJOI2014] 大融合](https://www.luogu.com.cn/problem/P4219) LCT 子树信息维护。 一般而言，对虚子树信息单独记一个数组或者 `set` 来维护子树信息，然后再 `push_up` （也叫 `maintain`） 操作中维护子树信息。 思考什么操作会影响虚子树信息： 1. `rotate` 和 `splay` 操作：没有虚边和实边的切换。无需维护。 2. `access` 操作，会将其中一条实边变为虚边，将一条虚边变为实边，所以维护变化量。 3. `link` 操作：因为连接是虚边连接，所以要更新信息。 4. `cut` 操作：切掉的是实边，无需维护。 注意事项：**此处的 `link` 操作要注意两个点都要 `make_root`**，因为如果不 `make_root` 的话，指向的点的祖先链就无法更新。 ### [BS 2018 -- 【BZOJ3306】树](https://oj.bashu.com.cn/code/problempage.php?problem_id=2018) 题意： 给定一棵大小为 $n$ 的有根点权树，支持以下操作: - 换根 - 修改点权 - 查询子树最小值 思路和上一题一样，只不过信息变为子树最小值，是半群信息。由于没有逆元，所以需要用一个 `set` 存储每个虚子树的信息。 _比较令我疑惑的一点：写完之后交上去 RE 了，经过我不断地调试之后，发现 `make_root` 中 `access` 之前再进行一次 `access` 就可以 AC 了。完全不理解是为什么。_ ### [P6292 区间本质不同子串个数](https://www.luogu.com.cn/problem/P6292) SAM 上弄 LCT 充当 ODT 的题目，但是要区间加等差数列。 首先离线扫描线定右端点维护变化量。设当前点为 $cu$。那我们就是要讨论每一个在 $cu$ 结尾的每一个后缀的影响。 #### 我们将后缀按 endpos 等价类划分，那么划分的每一段后缀上一次出现的位置相同。考虑每一段后缀，贡献可以分成原本后缀的贡献，减去重复的贡献。 原本的贡献：画个图可以知道，越往左边贡献越大（包含的后缀数量越多），到达最左边后贡献保持不变。也就是一段区间加，然后加一段公差为 $-1$ 的等差数列。 重复的贡献：重复的贡献是类似的。只不过权值要取相反数。 具体地：设当前点为 $cu$，该 endpos 类上一次出现的点为 $pla$，endpos 类最短后缀长度为 $l$，最长后缀长度为 $r$，则有： 1. $[cu-r+1,cu-l+1]$ 加一段首项为 $r-l+1$，末项为 $1$，公差为 $-1$ 的等差数列。 2. $[1,cu-r]$ 区间加 $r-l+1$。 $pla$ 不为 $0$ 时： 3. $[pla-r+1,pla-l+1]$ 加一段首项为 $-(r-l+1)$，末项为 $-1$，公差为 $1$ 的等差数列。 4. $[1,pla-r]$ 区间加 $-(r-l+1)$。 #### 发现这若干段后缀恰好对应 SAM 上的 Fail 链，所以暴力的做法就是直接跳 Fail 链求解。 如何优化？这若干段后缀一定是连续且不交的，**当 $pla$ 相同时完全可以合并成一个段考虑**。借用 ODT 和 LCT 的思想，我们暴力跳每一个后缀 endpos 块然后合并的复杂度是 $O(n\log n)$ 的。 #### 所以我们对 SAM 的 Fail 用 LCT 维护。每次 `access` 时维护当前链即可。 具体地：LCT 的每个 Splay 内维护后缀的最长和最短长度，以及上一次出现的位置。前者 `push_up` 维护，后者打标记 `push_down` 维护。在 `access` 时，我们要维护的是切掉链的上半部分的信息，对应辅助树中是结点加上左儿子的贡献。直接取其更新即可。 _然后代码就神奇的 WA 了。_ 一开始我还以为是 SAM 或是 LCT 写错了，最后发现全部是区间加等差数列的问题。 #### 区间加等差数列的注意事项： 1. 永久化标记，每个点记录所有标记的首项和以及公差和。 2. **在进入右子树的时候要特别小心**。讨论一下 $A$ 和 $mid+1$ 之间的关系，如果 $A\le mid+1$，那么首项要随之变化，并且传到右子树的 $A'$ 是 $mid+1$；否则不用变化。 3. 最后查询时记得加上区间加标记。 ### [BS 1781 -- 【BZOJ3514】GERALD07加强版](https://oj.bashu.com.cn/code/problempage.php?problem_id=1781) 题意：$n$ 个点 $m$ 条边的无向图，询问保留图中编号在 $[l,r]$ 的边的时候图中的联通块个数。 扫描线右端点维护后缀区间变化量。连通块个数等于生成树的点数量减去边数量。那本题中只需要维护边数量即可。 那么就可以思考我们应该保留哪些边作为生成树的边。 每条边的生效区间是平衡的，越早进入的边，应该越早删去。按边权从小到大加边，我们维护边编号的最大生成树。也就是在 LCT 中把最小的边删去。 考虑每一条边对后缀区间的贡献。 发现每一条边的生效区间为**加入的时间**一直到被**删去的时间**。 那么查询就是在右端点的边加入完后，此时生成树中在$[l,r]$ 区间的边。暴力直接上树套树。有没有更优秀的做法？ 1. 注意到只需要维护单点加，区间和的可持久化部分。上个主席树。 2. ~~分块。~~ 3. 每一条边是在其时间加入的。所以考虑当前时间时，后面的边是不需要考虑的。所以我们可以维护每一条边生效区间的右端点的位置（记作 $R_i$），到时就查区间有多少 $R_i>=r$ 的点。也是上主席树。 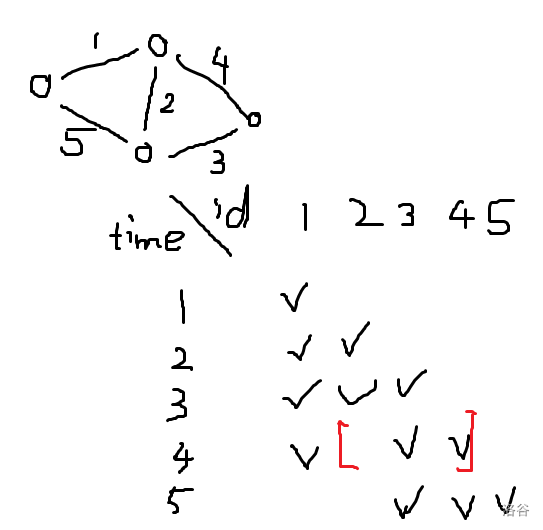 例子：$\text{time}$ 是边的生效区间。比如说查 $[2,4]$ 的边，就是红色区间的边数量。