【树状数组】学习笔记

本文中，为了避免歧义，定义：

- $n$：数据数量。
- $a_1 \sim a_n$ 原始数组。
- $b_1 \sim b_n$ 树状数组。

# 引入

给你一个数列 $a_1 \sim a_n$，你需要实现两个函数：
- 单点修改：将数列中的一个数值加 $x$。
- 区间查询：求出序列中前几个数的和。

如果用暴力或者前缀和显然是不行的，考虑优化。

# 理论
## 树状数组的原理

对于这个数列：
|$1$|$0$|$4$|$6$|$5$|$2$|$14$|$3$|$4$|$6$|$13$|$2$|$1$|$9$|$5$|$12$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|

可以把他相邻两个数求和，并归为新的一层，一直这样直到只剩下一个数字。

||||||||||||||||$87$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
||||||||$35$||||||||$52$|
||||$11$||||$24$||||$25$||||$27$|
||$1$||$10$||$7$||$17$||$10$||$15$||$10$||$17$|
|$1$|$0$|$4$|$6$|$5$|$2$|$14$|$3$|$4$|$6$|$13$|$2$|$1$|$9$|$5$|$12$|

他们的关系是这样的：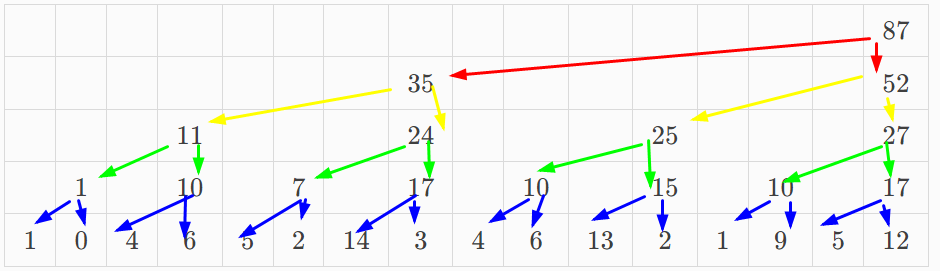
![](https://cdn.luogu.com.cn/upload/image_hosting/qw8i97ye.png)
这样就可以用额外计算出的数来优化时间。

到这个时候，求区间的和操作就可以找一些上面的大数，再拿下面的小数凑整。

比如计算前 $13$ 个只需要这些标红数字即可：

||||||||||||||||$87$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
||||||||$\color{red}35$||||||||$52$|
||||$11$||||$24$||||$\color{red}25$||||$27$|
||$1$||$10$||$7$||$17$||$10$||$15$||$10$||$17$|
|$1$|$0$|$4$|$6$|$5$|$2$|$14$|$3$|$4$|$6$|$13$|$2$|$\color{red}{1}$|$9$|$5$|$12$|

大大优化了运算速度。

这里注意到比如我想求前三个的和，那么第四行第二个数用不到，求前四个和时用第三行第一个更优，所以第四行第二个数没有任何用处。像这样无意义的数据还有很多，每行的第偶数个数据都没用，可以删掉。

||||||||||||||||$87$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
||||||||$35$|||||||||
||||$11$||||||||$25$|||||
||$1$||||$7$||||$10$||||$10$|||
|$1$||$4$||$5$||$14$||$4$||$13$||$1$||$5$||

这时候，每一列恰好都只有一个数，我们把每个数取出来组成一个数组：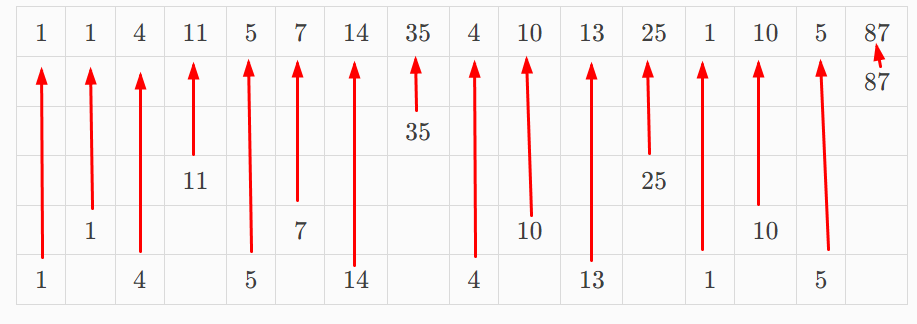
![](https://cdn.luogu.com.cn/upload/image_hosting/p4aoimmb.png)
|$1$|$1$|$4$|$11$|$5$|$7$|$14$|$35$|$4$|$10$|$13$|$25$|$1$|$10$|$5$|$87$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|

这个数组就是树状数组，里面的每一个元素都对应着一个区间和。

求和时，只需要找到对应的区间相加求和即可。

修改时，只需要找到向上包含它的区间再修改。

## $\operatorname{lowbit}$ 函数

$\operatorname{lowbit}(x)$ 可以求出 $x$ 在二进制下最低位代表哪个数字。

比如二进制数字 $10010100100$（十进制 $1188$），它的最低位是 $10010100\color{red}{1}\color{black}{00}$，所代表的数就是 $10010100\color{red}100$。二进制数 $100$ 对应的十进制数就是 $4$，所以$\operatorname{lowbit}(1188)=4$。

代码使用位运算来完成。

```cpp
int lowbit(int x)
{
    return x&(-x);
}
```
证明很简单，自己按位与自己的反码，除了最低有效位其他都会直接抵消。

## 使用 $\operatorname{lowbit}$ 实现树状数组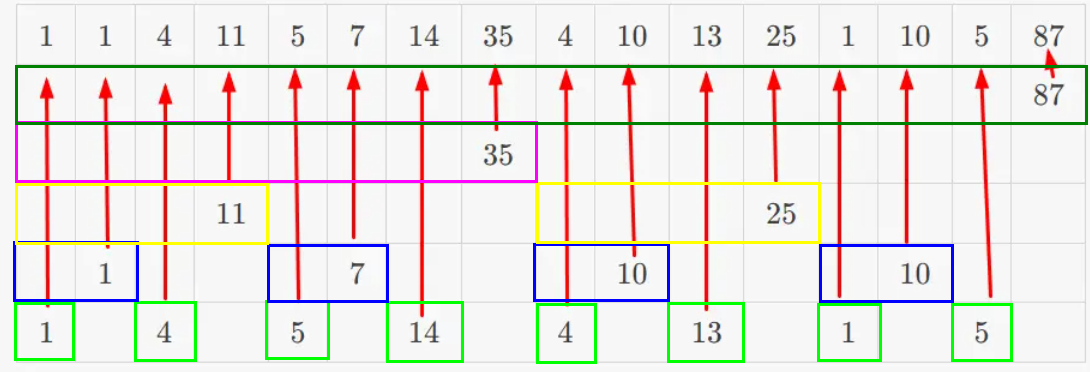

![](https://cdn.luogu.com.cn/upload/image_hosting/i3entxjw.png)

观察树状数组，最后一行的序列长度都为 $1$，而这些区间对应的树状数组序号的 $\operatorname{lowbit}$ 也为 $1$。倒数第二行的序列长度为 $2$，他们对应序号的 $\operatorname{lowbit}$ 也为 $2$。

其他的几行也是如此，依次是 $2,4,8,16,\cdots$ 依次是二的整数次幂。

比如 $b_{14}$，它对应的序列长度就是  $\operatorname{lowbit}(14)=4$。其他也是同理。

也就是说，$b_i$ 对应的序列就是长度为 $\operatorname{lowbit}(i)$ 且以 $i$ 结尾的序列。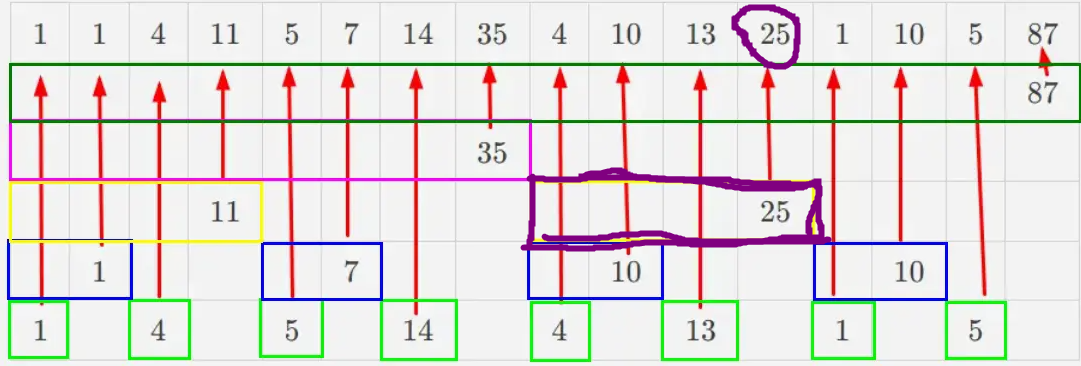

![](https://cdn.luogu.com.cn/upload/image_hosting/qh9y8qtp.png)

这个时候，如果我们要求前 $14$ 个数的和，$14-\operatorname{lowbit}(14)=12$，那么，只需要计算 $b_{14}$ 加上前十二个数的和就好了。计算前十二个数的和可以仿照同样的办法。

求解过程可记作：
$$
\operatorname{sum}(pos) = \begin{cases}
  0 & pos \le 0\\
  b_{pos}+ \operatorname{sum}(pos-\operatorname{lowbit}(pos))& pos>0\\
\end{cases}

也可以不用递归，不用递归的版本也很好写。

- 递归版本
```cpp
int sum(int pos)
{
    if(pos<=0)
	{
		return 0; 
	}
    return b[pos]+sum(pos-lowbit(pos));
}
```
- 非递归版本
```cpp
int sum(int pos)
{
    int cnt=0;
    while(pos>0)
	{
        cnt+=t[pos];
        pos-=lowbit(pos);
    }
    return cnt;
}
```
---
还有一个性质，就是 $b_i$ 正上方的序列刚好就是 $b_{i+\operatorname{lowbit}(i)}$。

所以只要在修改的时候不断加上 $\operatorname{lowbit}(i)$ 就可以找到包含自己的所有序列进行修改。

```cpp
void add(int pos,int x)//将第 pos 加上 x 并更新树状数组相关的元素
{
    while(pos<=n)
	{
        t[pos]+=x;
        pos+=lowbit(pos);
    }
}
```

# 例题

## [【单点修改】&【求区间和】](https://www.luogu.com.cn/problem/P3374)

很板的树状数组，不妨在建树的时候输入一个 $a$ 把他当作单点修改操作。

```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
int t[1000005];
int lowbit(int x)
{
    return x&(-x);
}
void add(int pos,int x)
{
    while(pos<=n)
	{
        t[pos]+=x;
        pos+=lowbit(pos);
    }
}
int sum(int pos)
{
    int cnt=0;
    while(pos>0)
	{
        cnt+=t[pos];
        pos-=lowbit(pos);
    }
    return cnt;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		add(i,x);
	}
	while(m--)
	{
		int q;
		cin>>q;
		if(q==1)
		{
			int x,k;
			cin>>x>>k;
			add(x,k);
		}
		else
		{
			int l,r;
			cin>>l>>r;
			cout<<sum(r)-sum(l-1)<<'\n';
		}
	}
	return 0;
}

```

## [$\lfloor$区间修改$\rceil$&$\lfloor$单点查询$\rceil$](https://www.luogu.com.cn/problem/P3368)

可以考虑维护差分树状数组，利用差分思想来预处理出差分数组。

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		add(i,x);
		add(i+1,-x);
		/*
		可以理解为在 i~i 区间内加 x。
		*/
	}
	while(m--)
	{
		int q;
		cin>>q;
		if(q==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
			add(x,k);
			add(y+1,-k);
		}
		else
		{
			int x;
			cin>>x;
			cout<<sum(x)<<'\n';
		}
	}
	return 0;
}

```
## [$\lfloor$区间修改$\rceil$&$\lfloor$求区间和$\rceil$](https://www.luogu.com.cn/problem/P3372)

区间修改利用差分维护即可，重点看求区间和。

那么

$$
\begin{aligned}
\sum_{i=1}^{x} a_i  &= \sum_{i=1}^{1} b_i + \sum_{i=1}^{2} b_i + \sum_{i=1}^{3} b_i + \cdots \sum_{i=1}^{x} b_i  \\
&= b_1 \times x + b_2 \times (x-1) + b_3 \times (x-2) + \cdots + b_x \times 1 \\

&= (x+1) \sum_{i=1}^{x} d_i - 1 \times d_1 -2 \times d_2 + \cdots + x \times d_x \\

&=  (x+1) \sum_{i=1}^{x} d_i - \sum_{i=1}^{x} (i \times d_i)
\end{aligned}

$$
我们给两个 $\sum$ 都做一个树状数组就可以了。

```cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long					//开ll（偷懒写法
int n,m,a[1000005];						//要用数组输入来保存差分数组
int At[1000005];
int Bt[1000005];
int lowbit(int x)
{
    return x&(-x);
}
void Aadd(int pos,int x)
{
    while(pos<=n)
	{
        At[pos]+=x;
        pos+=lowbit(pos);
    }
}
int Asum(int pos)
{
    int cnt=0;
    while(pos>0)
	{
        cnt+=At[pos];
        pos-=lowbit(pos);
    }
    return cnt;
}

void Badd(int pos,int x)
{
    while(pos<=n)
	{
        Bt[pos]+=x;
        pos+=lowbit(pos);
    }
}
int Bsum(int pos)
{
    int cnt=0;
    while(pos>0)
	{
        cnt+=Bt[pos];
        pos-=lowbit(pos);
    }
    return cnt;
}
 /*
((y+1ll)*Asum(y)-Bsum(y))-((x+1ll)*Asum(x)-Bsum(x))
*/
int getSum(int p)
{
	return (p+1LL)*Asum(p)-Bsum(p);
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		Aadd(i,a[i]-a[i-1]);
		Badd(i,i*(a[i]-a[i-1]));
	}
	while(m--)
	{
		int q;
		cin>>q;
		if(q==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
			Aadd(x,k);
			Aadd(y+1,-k);
			Badd(x,k*x);
			Badd(y+1,-(k*(y+1)));
		}
		else
		{
			int x,y;
			cin>>x>>y;
			cout<<getSum(y)-getSum(x-1)<<'\n';
		}
	}
	return 0;
}
```
## [$\lfloor$权值树状数组求逆序对$\rceil$](https://www.luogu.com.cn/problem/P1908)

要离散化。

按价值从大到小排序，排完序之后用树状数组维护，每次把这个数的位置加入到树状数组中。之前加入的一定比后加入的大，然后在查询当前这个数前面位置的数（是前面位置的数，要当前这个数减1）。就是逆序对的个数了

求逆序对。设树状数组为 $t$。

检查多少组 $a_{j} \sim a_i(j <i )$ 逆序对。

检查 $a_1 \sim a_{i-1}$ 有几个大于 $a_i$ 的数。
 
  检查 $t_{a_i+1} \sim t_n$ 和为多少即可。

```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
int ans=0;
struct node
{
	int x;//原数 
	int id;//在原数组里的编号 
	int t;//离散化之后的数字 
}a[500005];
bool cmp(node x,node y)
{
	return x.x<y.x;
}
bool cmp2(node x,node y)
{
	return x.id<y.id;
}
int t[500005];
int n;
int lowbit(int x)
{
    return x&(-x);
}
void add(int pos,int x)
{
    while(pos<=n)
	{
        t[pos]+=x;
        pos+=lowbit(pos);
    }
}
int sum(int pos)
{
    int cnt=0;
    while(pos>0)
	{
        cnt+=t[pos];
        pos-=lowbit(pos);
    }
    return cnt;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i].x;
		a[i].id=i;
	}
	//-----------------------------抽象离散化 
	sort(a+1,a+1+n,cmp);
	int tot=1;
	for(int i=1;i<=n;)
	{
		int X=a[i].x;
		while(a[i].x==X)
		{
			a[i].t=tot;
			i++;
		}
		tot++;
	}
	sort(a+1,a+1+n,cmp2);
	//--------------------------- 
	for(int i=1;i<=n;i++)
	{
		int x=a[i].t;
		add(x,1);
		ans+=i-sum(x);
	}
	cout<<ans;
	return 0;
}
```

# 二维树状数组

可以维护二维数组。

一维树状数组套一维树状数组。

根一维很像，多了一个维度。比较麻烦的是区间求和，涉及了二维前缀和与二维差分。

单点修改：
```cpp
void add(int x,int y,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		for(int j=y;j<=m;j+=lowbit(j))
		{
			t[i][j]+=k;
		}
	}
}
```
求区间和：
$$
\sum_{i=1}^{x} \sum_{j=1}^{y} a_{i,j}
$$
```cpp
int sum(int x,int y)
{
	int cnt=0;
	for(int i=x;i>=1;i-=lowbit(i))
	{
		for(int j=y;j>=1;j-=lowbit(j))
		{
			cnt+=t[i][j];
		}
	}
	return cnt;
}
```

## $\lfloor$二维单点修改$\rceil$&$\lfloor$二维区间求和$\rceil$

没有原题，所以先规定一个题面来避免歧义：[problem](https://www.luogu.com.cn/problem/U511277)。

这里涉及了二维前缀和，求一个区间的和可以进行类似这样的操作：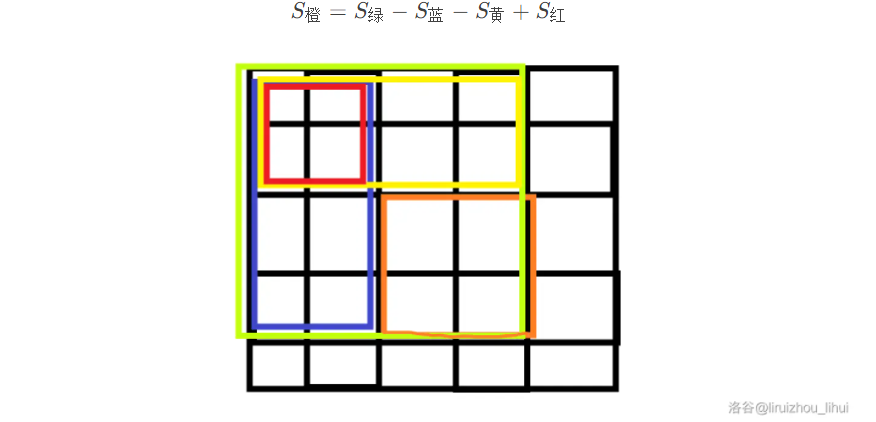

![](https://cdn.luogu.com.cn/upload/image_hosting/r6o21c9b.png)

先设原二维数组为 $a$，设前缀和数组 $sum$：

$$
sum_{i,j}= \sum_{x=1}^{i} \sum_{y=1}^j a_{x,y}
$$
根据容斥原理就可以推出来求区间和的公式：
![](https://wiki.33dai.cn/97uqbriwevuibl4xn8ofd.png)

```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,op;
int t[5000][5000];
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		for(int j=y;j<=m;j+=lowbit(j))
		{
			t[i][j]+=k;
		}
	}
}
int sum(int x,int y)
{
	int cnt=0;
	for(int i=x;i>=1;i-=lowbit(i))
	{
		for(int j=y;j>=1;j-=lowbit(j))
		{
			cnt+=t[i][j];
		}
	}
	return cnt;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>m;
	while(cin>>op)
	{
		if(op==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
			add(x,y,k);
		}
		if(op==2)
		{
			int x,y,z,t;
			cin>>x>>y>>z>>t;
			cout<<sum(z,t)-sum(x-1,t)-sum(z,y-1)+sum(x-1,y-1)<<"\n";
		}
	}
	return 0;
}
```