四边形不等式（决策单调性）（原 PPT 备份） 最后更新于 2025-05-01 20:08:27

[原 PPT](https://typst.app/project/rVumQEfKHeONSICKOUmkYa) 因为 typst 上太难弄链接了，于是习题只在这里放。 理论上是我的 sky 课件，但是没讲。 updated on 2025.4.26 一周年纪念，回来看一眼。 typst 更新后因未知原因坠机，只能在这更新了（ ## 一、四边形不等式 \ 定义 1：已知 $w_{j,i}(1 \leq j < i \leq n)$，若对任意 $x_{1} \leq x_{2} \leq y_{1} \leq y_{2}$ 有 $w_{x_{1},y_{1}} + w_{x_{2},y_{2}} \leq w_{x_{1},y_{2}} + w_{x_{2},y_{1}}$，则称原函数满足四边形不等式。 定义 2：若对任意 $x,y(x \leq y)$ 有 $w_{x,y} + w_{x + 1,y + 1} \leq w_{x,y + 1} + w_{x,y + 1}$，则称原函数满足四边形不等式。 这两个定义是等价的。 - 若将定义 1 的 $a,b,c,d$ 分别设为 $x,x + 1,y,y + 1$，就是定义 2 的形式。 - 考虑对定义 2 使用数学归纳法，若对 $x_{1},x_{2},y_{1},y_{2}$ 与 $x_{2},x_{3},y_{1},y_{2}$ 已经满足四边形不等式，$x_{1},x_{3},y_{1},y_{2}$ 也满足四边形不等式，那么就可以由 $x,x + 1,y,y + 1$ 推至 $x,x',y,y + 1$，在 $y$ 方向同理。 证明： $\begin{aligned} w_{x_{1},y_{1}} + w_{x_{2},y_{2}} & \leq w_{x_{1},y_{2}} + w_{x_{2},y_{1}} \\ w_{x_{2},y_{1}} + w_{x_{3},y_{2}} & \leq w_{x_{2},y_{2}} + w_{x_{3},y_{1}} \\ w_{x_{1},y_{1}} + w_{x_{2},y_{2}} + w_{x_{2},y_{1}} + w_{x_{3},y_{2}} & \leq w_{x_{1},y_{2}} + w_{x_{2},y_{1}} + w_{x_{2},y_{2}} + w_{x_{3},y_{1}} \\ w_{x_{1},y_{1}} + w_{x_{3},y_{2}} & \leq w_{x_{1},y_{2}} + w_{x_{3},y_{1}} \end{aligned}$ 形象一点地来讲：  考虑这么一个方格，其中第 $(i,j)$ 格填的是 $w_{i,j}$。 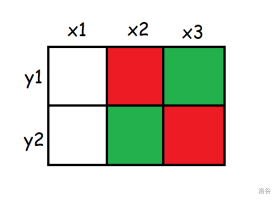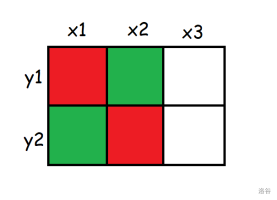 这两张图分别代表 $x_1,x_2,y_1,y_2$ 与 $x_2,x_3,y_1,y_2$ 的四边形不等式，其中红色部分对应不等式左边，绿色对应不等式右边。（即红色部分之和 $\le$ 绿色部分之和） 将红绿两色部分分别加起来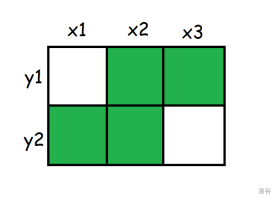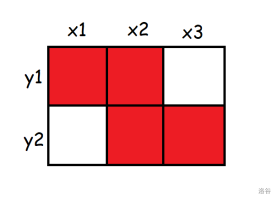：  由于红绿两色分别对应不等式的两侧，因此可以消去相同的部分，再加起来得：  也就是 $x_1,x_3,y_1,y_3$ 对应的四边形不等式。 由此，可得验证四边形不等式的代码如下： ```cpp for(int i=1;i<n;++i) for(int j=i;j<n;++j) assert(w(i,j)+w(i+1,j+1)<=w(i,j+1)+w(i+1,j)); ``` 如果程序没有出现报错，那么四边形不等式成立。 在考场上一般用这种方法判定四边形不等式。 ## 二、关于决策单调性 \ 首先考虑一个问题：已知 $w_{(j,i)(1 \leq j < i \leq n)}$，求所有 $f_{i} = \min\limits_{j \leq i}w_{j,i}$，此时不考虑 DP 转移。 对于每个 $i$，令 $p_{i}$ 表示在计算 $f_{i}$ 时的最优决策点，即当 $j = p_{i}$ 时 $w_{j,i} = f_{i}$，不妨设 $p_{i}$ 为第一个满足条件的点。 **决策单调性：**$\forall i < i',p_{i} \leq p_{i'}$ 注意，有了决策单调性之后还是要计算 $f_{i} = \min\limits_{p_{i - 1} \leq j \leq i}w_{j,i}$，如果 $p_{1} = p_{2} = \ldots = p_{n} = 1$，那么暴力计算的计算量与原来的一样，所以要想别的方法优化。 其实由四边形不等式可以推知决策单调性。 考虑用反证法，设 $\exists i' < i,p_{i'} > p_{i}$。 对 $p_{i},p_{i'},i',i$ 应用四边形不等式可得\ $\begin{aligned} w_{p_{i},i'} + w_{p_{i'},i} & \leq w_{p_{i'},i'} + w_{p_{i},i} \end{aligned}$ 由于上面的定义，$w_{p_{i},i'} > w_{p_{i'},i'},w_{p_{i'},i} \geq w_{p_{i},i}$ 显然不符合，故决策单调性成立。 对于以上内容，将 $\min$ 换为 $\max$ 后也可以用类似的方法证明。 具体地，将四边形不等式换为 $w_{x_1,y_1}+w_{x_2,y_2} \ge w_{x_1,y_2}+w_{x_2,y_1}$，将 $f$ 对应的式子换为 $f_i=\max\limits _{j \le i}w_{j,i}$，然后同样运用反证法即可。 这种情况下判定代码如下： ```cpp for(int i=1;i<n;++i) for(int j=i;j<n;++j) assert(w(i,j)+w(i+1,j+1)>=w(i,j+1)+w(i+1,j)); ``` 为方便考虑，以下内容只考虑 $\min$ 的形式，$\max$ 是同理的。 --- 对于之前的问题，若满足决策单调性，有几个方法优化。 0. **单调队列与斜率优化** 和主题无关，不讲。 1. **分治** 对于每个区间 $\lbrack l,r\rbrack$，设它的中点为 $m$，先求出 $p_{m}$ 设区间 $\lbrack l,mid)$ 的中点为 $m_{l}$，区间 $(mid,r\rbrack$ 的中点为 $m_{r}$，由于 $p\left( m_{l} \right) \leq p(m) \leq p\left( m_{r} \right)$，所以只需在求 $p_{m_{l}}$ 时计算 $1\sim\min(p_{m},m_{l} - 1)$，在求 $p_{m_{r}}$ 时计算 $p_{m}\sim m_{r} - 1$，递归做即可。\ 下一层计算量至多为 $m_{r} + 1 = O(n)$，同理每一层均为 $O(n)$。这种方法共递归 $O\left( \log n \right)$ 层，所以总计算量为 $O\left( n\log n \right)$。 参考代码： ```cpp void solve(int l,int r,int L,int R){ //l与r代表要求区间[l,r]的f，L与R代表p的范围 int mid=(l+r)>>1; for(int i=L;i<=min(mid-1,R);++i) if(w(i,mid)<f[mid])f[mid]=w(i,mid),p[mid]=i; if(mid>l)solve(l,mid-1,L,p[mid]); if(mid<r)solve(mid+1,r,p[mid],R); } ``` 2\. **单调队列 + 二分** 考虑每一个决策点（即每一个 $j$），由于 $p_{i} \leq p_{i + 1}$，这个 $j$ 能够作为一段 $i$ 的 $p_{i}$，然后就永远不行了。 二分这一段 $i$ 的范围（不妨设为 $\left\lbrack l_{j},r_{j} \right\rbrack$），然后用单调队列维护目前可行的所有决策点。 具体来说，对每个 $i$，先弹出过时的队头（即 $r_{j} < i$ 的队头），拿剩下的队头 $j$ 计算 $f(i)$，然后尝试将 $i$ 入队。 - 如果队列为空，直接入队，此时 $l_{i} = i + 1,r_{i} = n$。 - 否则，设队尾为 $j'$，如果 $i$ 比 $j'$ 劣，将 $i$ 拼在 $j'$ 的后面，即 $l_{i} = r_{j} + 1,r_{i} = n$。注意到这种情况需要入队当且仅当 $r_{j'} < n$，由于在处理后面的内容时可能将 $r_{j'} = n$ 的队尾出队，因此可能需要考虑。 - 否则，分两类讨论 $i$ 比 $j'$ 优，需要入队的情况： - 若对 $\left\lbrack l_{j'},r_{j'} \right\rbrack$，$i$ 均比 $j'$ 更优，将 $j'$ 出队。由于 $i \geq j'$ 与决策单调性，只需要判断 $w_{j',l_{j'}} > w_{i,l_{j'}}$ 即可，这种情况可能会多次出现。 - 若对 $\left\lbrack l_{j'},r_{j'} \right\rbrack$ 中的一部分，$i$ 比 $j'$ 更优，将 $i$ 入队并用二分判断 $i$ 开始比 $j'$ 更优的位置，设这个位置为 $k$ 则 $r_{q'} = k - 1,l_{i} = k,r_{i} = n$。 代码实现如下：（其实有很多版本，但是为了后面的内容先用这一版讲） ```cpp deque<int> q; l[1]=1,r[1]=n; q.push_back(1); for(int i=2;i<=n;++i){ while(!q.empty()&&i>r[q.front()])q.pop_front();//处理过时元素 ans[i]=w(q.front(),i),fr[i]=q.front(); while(!q.empty()&&w(q.back(),l[q.back()])>=w(i,l[q.back()])) q.pop_back();//处理 i 完全优于 j' 的情况 if(q.empty()){//处理队列为空的情况 q.push_back(i); l[i]=i+1,r[i]=n; } else if(w(q.back(),r[q.back()])<w(i,r[q.back()])){ if(r[q.back()]<n){//将i接在j'后面 q.push_back(i); l[i]=r[q.back()]+1,r[i]=n; } } else{ int L=l[q.back()],R=r[q.back()],mid,p; while(R>=L){//二分 mid=(R+L)/2; if(w(q.back(),mid)>=w(i,mid))p=mid,R=mid-1;//记录i开始优于j'的时间 else L=mid+1; } r[q.back()]=p-1,l[i]=p,r[i]=n; q.push_back(i); } } ``` 3\. **其它做法** SMAKW 等，可以做到 O (n)。 [例题](https://www.luogu.com.cn/problem/CF1423M) ### 例题 1：[lightning conductor](https://www.luogu.com.cn/problem/P3515) \ 给定一个长度为 $n$ 的序列 $\left\{ a_{n} \right\}$，对于每个 $i \in \lbrack 1,n\rbrack$，求出一个最小的非负整数 $p$，使得 $\forall j \in \lbrack 1,n\rbrack,a_{j} \leq a_{i} + p - \sqrt{|i - j|}$ $1 \leq n \leq 5 \times 10^{5}$，$0 \leq a_{i} \leq 10^{9}$。 解析：显然 $p = \max\limits_{(j)\left( a_{j} - a_{i} + \sqrt{|i - j|} \right)}$。 考虑拆掉 $\sqrt{i - j}$ 中的绝对值，于是分 $1 \leq j \leq i$ 与 $i \leq j \leq n$ 两段考虑，可以先处理完一段的情况后将序列翻转再做一次，此处考虑 $1 \leq j \leq i$ 的情况，因为决策单调性中的 $w_{j,i}$ 函数满足 $j \leq i$。 但是决策单调性要求 $\min\limits_{j \leq i}w_{j,i}$，所以设 $w_{j,i} = - \left( a_{j} - a_{i} + \sqrt{i - j} \right)$。 考虑对它证四边形不等式，将 $w_{j,i}$ 套入四边形不等式中得 $\begin{aligned} {r} - \left( a_{x_{1}} - a_{y_{1}} + \sqrt{y_{1} - x_{1}} \right) - \left( a_{x_{2}} - a_{y_{2}} + \sqrt{y_{2} - x_{2}} \right) \ \leq - \left( a_{x_{1}} - a_{y_{2}} + \sqrt{y_{2} - x_{1}} \right) - \left( a_{x_{2}} - a_{y_{1}} + \sqrt{y_{1} - x_{2}} \right) \end{aligned}$ 化简得 $- \sqrt{y_{1} - x_{1}} - \sqrt{y_{2} - x_{2}} \leq - \sqrt{y_{2} - x_{1}} - \sqrt{y_{1} - x_{2}}$ 即 $\sqrt{y_{1} - x_{1}} + \sqrt{y_{2} - x_{2}} \geq \sqrt{y_{2} - x_{1}} + \sqrt{y_{1} - x_{2}}$。 两边同时平方得 $\begin{array}{r} y_{1} - x_{1} + y_{2} - x_{2} + 2\sqrt{\left( y_{1} - x_{1} \right)\left( y_{2} - x_{2} \right)} \\ \geq y_{2} - x_{1} + y_{1} - x_{2} + 2\sqrt{\left( y_{2} - x_{1} \right)\left( y_{1} - x_{2} \right)} \end{array}$ 再化简得 $\begin{aligned} \left( y_{1} - x_{1} \right)\left( y_{2} - x_{2} \right) & \geq \left( y_{2} - x_{1} \right)\left( y_{1} - x_{2} \right) \\ y_{1}y_{2} + x_{1}x_{2} - x_{1}y_{2} - x_{2}y_{1} & \geq y_{1}y_{2} + x_{1}x_{2} - x_{1}y_{1} - x_{2}y_{2} \end{aligned}$ $\begin{aligned} x_{1}y_{2} + x_{2}y_{1} & \leq x_{1}y_{1} + x_{2}y_{2} \\ x_{1}\left( y_{2} - y_{1} \right) + x_{2}\left( y_{1} - y_{2} \right) & \leq 0 \\ \left( x_{1} - x_{2} \right)\left( y_{2} - y_{1} \right) & \leq 0 \end{aligned}$ 由 $x_{1} \leq x_{2}$，$y_{1} \leq y_{2}$，上面的式子显然成立，倒推回去即可证明原函数满足四边形不等式。 可以用分治或单调队列 + 二分解决。 对于二分队列做法，还存在更优的复杂度。 考虑算法本身的复杂度，其瓶颈在于二分判断一个数开始比另一个数优的位置，而在本题中可以通过解不等式解决。 具体来讲，$x$ 比 $y$ 优的位置即为满足下列不等式的所有整数 $j$：（默认只考虑一边） $\begin{aligned} a_{j} - a_{x} + \sqrt{j - x} & < a_{j} - a_{y} + \sqrt{j - y} \\ \sqrt{j - x} & \leq \sqrt{j - y} + a_{x} - a_{y} \end{aligned}$\ 设 $t = a_{x} - a_{y}$，则有\ $\begin{aligned} \sqrt{j - x} & \leq \sqrt{j - y} + t \\ j - x & \leq j - y + 2t\sqrt{j - y} + t^{2} \\ \frac{y - x - t^{2}}{2t} & \leq \sqrt{j - y}\begin{array}{r} \\ \left( \frac{y - x - t^{2}}{2t} \right) \end{array}^{2} + y \leq j \end{aligned}$ 取 $j = \left\lceil {\left( \frac{y - x - t^{2}}{2t} \right)^{2} + y} \right\rceil$ 即为 $x$ 开始比 $y$ 优的位置，时间复杂度 $O(n)$。 （可以使用这种方法通过所有斜率优化题，因为一条直线显然是凸的） ## 二、关于决策单调性 \ 考虑扩展之前的问题（求所有 $f_{i} = \min\limits_{j \leq i}w_{j,i}$）。 首先，考虑 dp 转移，即把与 $f_{j}$ 有关的东西放入 $w_{j,i}$ 中。 注意到在四边形不等式中任何只关于 $i$ 或 $j$ 的项都可以在证明中被消去。 严格来说，设 $w_{j,i} = w'_{j,i} + g_{j} + g_{i}$，而 $w'_{j,i}$ 满足四边形不等式，则 $w_{j,i}$ 满足四边形不等式。 证明： $\begin{aligned} w'_{x_{1},y_{1}} + w'_{x_{2},y_{2}} & \leq w'_{x_{1},y_{2}} + w'_{x_{2},y_{1}} \\ w'_{x_{1},y_{1}} + w'_{x_{2},y_{2}} + g_{x_{1}} + g_{x_{2}} + g_{y_{1}} + g_{y_{2}} & \leq w'_{x_{1},y_{2}} + w'_{x_{2},y_{1}} + g_{x_{1}} + g_{x_{2}} + g_{y_{1}} + g_{y_{2}} \\ w_{x_{1},y_{1}} + w_{x_{2},y_{2}} & \leq w_{x_{1},y_{2}} + w_{x_{2},y_{1}} \end{aligned}$ 所以就能用与之前类似的方法用四边形不等式了。 ### 例题 2：[诗人小 G](https://www.luogu.com.cn/problem/P1912) 小 G 是一个出色的诗人，经常作诗自娱自乐。但是，他一直被一件事情所困扰，那就是诗的排版问题。 一首诗包含了若干个句子，对于一些连续的短句，可以将它们用空格隔开并放在一行中，注意一行中可以放的句子数目是没有限制的。 小 G 给每首诗定义了一个行标准长度（行的长度为一行中符号的总个数），他希望排版后每行的长度都和行标准长度相差不远。 显然排版时，不应改变原有的句子顺序，并且一个句子只能在一行内。 在满足上面两个条件的情况下，小 G 对于排版中的每行定义了一个不协调度， 为这行的实际长度与行标准长度差值绝对值的 P 次方，而一个排版的不协调度为所有行不协调度的总和。 请你对几首首诗进行排版，使得排版后的诗不协调度尽量小，并输出排版的结果。 解析：不协调度只与每个句子的长度有关，所以设每个句子的长度为 $l_{1},l_{2},\ldots l_{n}$，其前缀和为 $s_{1},s_{2},\ldots s_{n}$ 由题可知 $w_{j,i} = f_{j} + |\left( s_{i} - s_{j - 1} + i - j \right) - l|^{P}$，同样考虑对它证四边形不等式。 此处使用第二个定义，得 $\begin{array}{r} f_{x} + |s_{y} - s_{x - 1} + y - x - l|^{p} + f_{x + 1} + |s_{y + 1} - s_{x} + y - x - l|^{p} \\ \leq f_{x} + |s_{y + 1} - s_{x - 1} + y + 1 - x - l|^{p} + f_{x + 1} + |s_{y} - s_{x} + y - x - 1 - l|^{p} \end{array}$ 两边同时消掉 $f_{x} + f_{x + 1}$ 得： $\begin{array}{r} |s_{y} - s_{x - 1} + y - x - l|^{p} + |s_{y + 1} - s_{x} + y - x - l|^{p} \leq \\ |s_{y + 1} - s_{x - 1} + y + 1 - x - l|^{p} + |s_{y} - s_{x} + y - x - 1 - l|^{p} \end{array}$ 设 $k = s_{y} - s_{x - 1} + y - x - l$，$k' = k + a_{y + 1} + 1$，则 $\begin{aligned} |k|^{P} + |k + a_{y + 1} + a_{x}|^{P} & \leq |k + a_{y + 1} + 1|^{P} + |k + a_{x} - 1|^{P} \\ |k|^{P} - |k + a_{x} - 1|^{P} & \leq |k + a_{y + 1} + 1| - |k + a_{y + 1} + a_{x}|^{P} \\ |k|^{P} - |k + a_{x} - 1|^{P} & \leq |k'| - |k' + a_{x} - 1|^{P} \end{aligned}$ 考虑函数 $y = |x|^{P}$ 的性质，从图像入手。 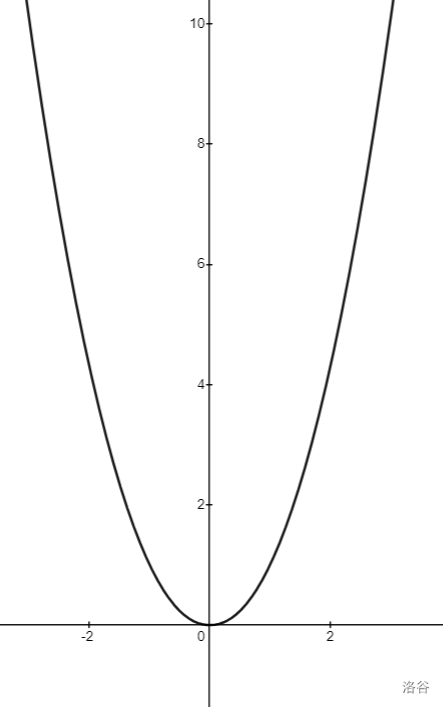 [对应图表](https://www.desmos.com/calculator/pf3hbfgttk?lang=zh-CN) 这个图像的斜率单调不减，因此 $k\sim\left( k + a_{x} - 1 \right)$ 部分的减小值会大于 $k'\sim\left( k' + a_{x} - 1 \right)$ 部分，即原不等式成立。 （如果学过导数，那么可以知道导数单调增，就不必如此大费周章了） 由于求 $w_{j,i}$ 需要之前的结果，因此只能用单调队列 + 二分。 ## 二、关于决策单调性 \ 考虑把状态维数从一维升到二维，但二维 DP 种类较多，需结合题目分析。 此处要求 $w_{i,j}$ 满足区间包含单调性，即对任意 $a \leq b \leq c \leq d,w_{b,c} \leq w_{a,d}$。 ### 例题 3：[Optimal Binary Search Tree](https://www.luogu.com.cn/problem/UVA10304) \ 求一棵有 $N$ 个节点的**二叉搜索树**，使 $\sum\limits_{i = 1}^{(N)\left( a_{i} \times d_{i} \right)}$ 最小，其中 $a_{i}$ 为点的权值，$d_{i}$ 为深度（根节点深度为 0）。 （这题是四边形不等式优化 DP 的起源） 解析：设 $s_{i}$ 表示 $a_{i}$ 的前缀和，$f_{i,j}$ 表示区间 $\lbrack i,j\rbrack$ 的最小代价。考虑枚举区间 $\lbrack i,j\rbrack$ 对应最优二叉搜索树的根 $k$，则 $f_{i,j} = w_{i,j} + \min\limits_{i \leq k < j}\left ( f_{i,k} + f_{k + 1,j} - a_{k} \right)$，其中这道题中的 $w_{i,j} = s_{j} - s_{i - 1}$。考虑优化，但是 $f_{i,j}$ 不能省，只能考虑减少枚举 $k$ 次数。 首先考虑证明 $f_{i,j}$ 满足四边形不等式，即对任意 $a \leq b \leq c \leq d$ 有 $f_{a,c} + f_{b,d} \leq f_{a,d} + f_{b,c}$。根据之前的讨论，可以不考虑 $s_{j} - s_{i - 1}$ 的部分。 设 $k_{0} = p_{a,d}$，$k_{1} = p_{b,c}$，分两种情况考虑。 - 若 $k_{0} \in \lbrack b,c\rbrack$ - &#x20;若 $k_{1} \in \left\lbrack a,k_{0} \right\rbrack$ 则&#x20; $\begin{aligned} f_{a,d} + f_{b,c} & = f_{a,k_{0}} + f_{k_{0} + 1,d} + f_{b,k_{1}} + f_{k_{1} + 1,c} + w_{a,d} + w_{b,c} - a_{k_{0}} - a_{k_{1}} \\ & \geq f_{a,k_{0}} + f_{k_{1} + 1,c} + f_{b,k_{1}} + f_{k_{0} + 1,d} + w_{a,c} + w_{b,d} - a_{k_{0}} - a_{k_{1}} \end{aligned}$ &#x20;由于无法直接处理，考虑归纳，则有&#x20; $\begin{aligned} & f_{a,k_{0}} + f_{k_{1} + 1,c} + f_{b,k_{1}} + f_{k_{0} + 1,d} + w_{a,c} + w_{b,d} \\ \geq & f_{a,k_{1}} + f_{k_{1} + 1,c} + f_{b,k_{0}} + f_{k_{0} + 1,d} + w_{a,c} + w_{b,d} \\ \geq & f_{a,c} + f_{b,d} \end{aligned}$ &#x20;由于当 $a = b$ 或 $c = d$ 时四边形不等式成立，所以归纳成立。\ 此处要求 $w_{i,j}$ 满足四边形不等式。 - 若 $k_{1} \in \left\lbrack k_{0} + 1,b \right\rbrack$，方法与上面类似。 - 否则， $\begin{aligned} f_{a,d} + f_{b,c} & = f_{a,k_{0}} + f_{k_{0} + 1,d} + f_{b,c} + w_{a,d} - a_{k_{0}} - a_{k_{1}} \\ & \geq f_{a,c} + f_{b,k_{0}} + f_{k_{0} + 1,d} + w_{a,d} - a_{k_{0}} - a_{k_{1}} \\ & \geq f_{a,c} + f_{b,k_{0}} + f_{k_{0} + 1,d} + w_{b,d} - a_{k_{0}} - a_{k_{1}} \\ & \geq f_{a,c} + f_{b,d} \end{aligned}$ 在这题中，$w_{i,j}$ 显然满足四边形不等式与区间包含单调性，因此 $f_{i,j}$ 满足四边形不等式。 根据前人的智慧，我们知道 $p_{i,j - 1} \leq p_{i,j} \leq p_{i + 1,j}$。 先证明 $p_{i,j - 1} \leq p_{i,j}$。对每一个 $i$，设 $f'_{k,j} = f_{i,k} + f_{k + 1,j} + w_{i,j}$，显然 $f'_{k,j}$ 满足四边形不等式，所以对 $f_{i,j} = \min\limits_{k = i}^{j}f'_{k,j}$ 应用一开始的结论即可，证明 $p_{i,j} \leq p_{i + 1,j}$ 的过程类似。 于是可以写出代码如下： ```cpp for(int i=1;i<=n;++i) p[i][i]=i; for(int l=2;l<=n;++l) for(int i=1,j=l;j<=n;++i,++j){ for(int k=p[i][j-1];k<=p[i+1][j];++k) if(f[i][k]+f[k+1][j]<f[i][j])f[i][j]=f[i][k]+f[k+1][j]-a[k],p[i][j]=k; f[i][j]+=s[j]-s[i-1]; } ``` 对于任意一个区间长度 $l$，决策量均为 $\sum\limits_{i}^{n - l + 1}( p_{i + 1,i + l} - p_{i,i + l - 1}) = n$。 因为区间长度共 $n$ 种，因此总时间复杂度 $O\left( n^{2} \right)$。 可以看出，$a_{k}$ 同样在证明中没什么变化，可以忽略。 满足四边形不等式的矩阵称为蒙日矩阵，可以类似地在 $O(n^2)$ 时间内计算蒙日矩阵乘法。（此处矩阵乘法为 $( \min , +)$ 卷积形式） upd: 含有凸函数的 $( \min , +)$ 卷积一般都会使用决策单调性优化。 ### 例题 4：[Yet Another Minimization Problem](https://www.luogu.com.cn/problem/CF868F) \ 给定一个长度为 $n$ 的序列 $a$，要把它分成 $k$ 个子段。每个子段的费用是其中相同元素的对数。求所有子段的费用之和的最小值。 $2 \leq n \leq 10^{5}$，$2 \leq k \leq \min(n,20)$，$1 \leq a_{i} \leq n$。 解析：此时的形式与一维类似，考虑沿用一维的方法，设 $f_{i,j}$ 表示把序列前 $i$ 个分成 $j$ 段的最小代价，$w_{j,i}$ 表示子段 $\lbrack j,i\rbrack$ 的费用 显然 $f_{i,j} = \min\limits_{(1 \leq k < i)\left( f_{k - 1,j - 1} + w_{k,i} \right)}$。 并且\ $\begin{aligned} w_{x,y} + w_{x + 1,y + 1} & = 2w_{x + 1,y} + \sum\limits_{i = x + 1}^{y}\left\lbrack a_{i} = a_{y + 1} \right\rbrack + \sum\limits_{i = x + 1}^{y}\left\lbrack a_{i} = a_{x} \right\rbrack \\ w_{x,y + 1} + w_{x + 1,y} & = 2w_{x + 1,y} + \sum\limits_{i = x + 1}^{y}\left\lbrack a_{i} = a_{y + 1} \right\rbrack + \sum\limits_{i = x + 1}^{y}\left\lbrack a_{i} = a_{x} \right\rbrack + \left\lbrack a_{x} \leq a_{y + 1} \right\rbrack \\ w_{x,y + 1} + w_{x + 1,y} & \leq w_{x,y} + w_{x + 1,y + 1} \end{aligned}$ 所以 $w_{j,i}$ 满足四边形不等式。 可以用一样的反证法证明决策单调性，由于不用这一维的决策，可以之前的方法求解，时间复杂度 $O\left( nk\log_{2}n \right)$。 可是这么做有个问题：如何 $O(1)$ 计算 $w_{j,i}$？ 根据莫队的知识，可以利用左右移动区间端点快速求解（我也不知道什么其他的方法加速），考虑将这种思想用在分治做法上。 在分治到 $\lbrack l,r\rbrack$，答案范围为 $\lbrack L,R\rbrack$ 时，需要先对所有 $L \leq i \leq \min(\text{mid},R)$ 计算 $w_{i,\text{mid}}$。 开始计算时要求区间为 $\lbrack L,L\rbrack$，在计算过程中共移动 $\min(\text{mid},R) - L$ 次。 计算完成后分治 $\left\lbrack l,\text{mid} - 1 \right\rbrack\left\lbrack L,p_{,j} \right\rbrack$，相当于移回 $\lbrack L,L\rbrack$，同样移动 $\min(\text{mid},R)$ 次。 分治结束后区间显然还在 $\lbrack L,R\rbrack$ 内，接下来分治 $\left\lbrack \text{mid} + 1,r \right\rbrack\left\lbrack p_{,j},R \right\rbrack$，需移动到 $p_{},p_{}$ 显然移动次数不超过 $2(R - L)$ 次。 整体时间复杂度仍为 $O\left( nk\log_{2}n \right)$。 计算 $w$ 函数的代码如下，其余与之前没什么区别： ```cpp int l0,r0,s[100005]; long long ans; long long w(int l,int r){ while(l0>l)--l0,ans+=s[a[l0]],++s[a[l0]]; while(r0<r)++r0,ans+=s[a[r0]],++s[a[r0]];//注意跟莫队一样先加后减 while(l0<l)--s[a[l0]],ans-=s[a[l0]],++l0; while(r0>r)--s[a[r0]],ans-=s[a[r0]],--r0; return ans; } ``` ### 例题 5：[\[IOI2000\] 邮局](https://www.luogu.com.cn/problem/P4767) 高速公路旁边有一些村庄。高速公路表示为整数轴，每个村庄的位置用单个整数坐标标识。没有两个在同样地方的村庄。两个位置之间的距离是其整数坐标差的绝对值。 邮局将建在一些，但不一定是所有的村庄中。为了建立邮局，应选择他们建造的位置，使每个村庄与其最近的邮局之间的距离总和最小。 你要编写一个程序，已知村庄的位置 $x_{1},\ldots x_{n}$ 和邮局的数量 $m$，计算每个村庄和最近的邮局之间所有距离的最小可能的总和。 考虑每个邮局控制的区间 $\lbrack i,j\rbrack$，由小学知识可得将邮局建在 $x_{\left\lfloor \frac{i + j}{2} \right\rfloor}$ 的位置最好。 设 $w_{i,j}$ 表示一个邮局控制 $\lbrack i,j\rbrack$ 时这段区间的最小距离和，$s_{i}$ 表示 $x_{i}$ 的前缀和，${m}_{i,j} = \left\lfloor \frac{i + j}{2}\right\rfloor$，则有 $\begin{aligned} w_{i,j} & = {x_{m}}_{i,j} \ast \left( {m}_{i,j} - i + 1 \right) - \left( {s_{m}}_{i,j} - s_{i - 1} \right) + \left( s_{j} - {s_{m}}_{i,j} \right) - {x_{m}}_{i,j} \ast \left( j - {m}_{i,j} \right) \\ & = {x_{m_{i,j}}\left( 2{m}_{i,j} + i + j + 1 \right)} + s_{i - 1} + s_{j} - 2{s_{m}}_{i,j} \end{aligned}$ 考虑证明 $w_{i,j}$ 满足四边形不等式，此处使用 $w_{i,j} + w_{i + 1,j + 1} \geq w_{i + 1,j} + w_{i,j + 1}$。 同样通过之前的方法消掉 $s_{i - 1} + s_{j}$。 先考虑 ${m}_{i,j},{m}_{i,j + 1},{m}_{i + 1,j},{m}_{i + 1,j + 1}$ 这四个数的关系。 - 若 $2|i + j$，则 ${m}_{i,j} = {m}_{i,j + 1} = {m}_{i + 1,j} = {m}_{i + 1,j + 1} - 1$ &#x20;转化为（下面的 $\LaTeX$ 懒得修了） upd: 好了&#x20; $\begin{array}{r} {x_{m_{i,j}}\left( 2{m}_{i,j} + i + j + 1 \right)} + x_{m_{i,j}+1}{\left( 2{m}_{i,j} + i + j + 5 \right)} - 2x_{{m}_{i,j} + 1} \geq 2{x_{m_{i,j}}\left( 2{m}_{i,j} + i + j + 2 \right)} \\ {x_{m_{i,j}}\left( 2{m}_{i,j} + i + j \right)} + x_{m_{i,j}}\left( 2{m}_{i,j} + i + j \right) + x_{m_{i,j}} + 3x_{{m}_{i,j} + 1} \\ \geq 2{x_{m}}_{i,j}\left( 2{m}_{i,j} + i + j \right) + 4{x_{m}}_{i,j} \\ x_{{m}_{i,j} + 1} \left( 2{m}_{i,j} + i + j \right) + {x_{m}}_{i,j} + 3x_{{m}_{i,j} + 1} \geq {x_{m_{i,j}}}\left( 2{m}_{i,j} + i + j \right) + 4{x_{m}}_{i,j} \end{array}$ &#x20;显然成立，故满足四边形不等式。 - 否则 ${}_{i,j} + 1 = {}_{i,j + 1} = {}_{i,j + 1} = {}_{i + 1,j + 1}$，证法类似。 可以继续用分治做，但还有更好的方法。 再次根据前人的智慧，可以知道 $p_{i,j - 1} \leq p_{i,j} \leq p_{i + 1,j}$。 $p_{i,j} \leq p_{i + 1,j}$ 之前已经证明过了，$p_{i,j - 1} \leq p_{i,j}$ 的证明如下： 考虑将 $f_{i,j}$ 对应的区间划分设为 $\left\lbrack a_{1},a_{2} - 1 \right\rbrack,\left\lbrack a_{2},a_{3} - 1 \right\rbrack,\ldots\left\lbrack a_{j},i \right\rbrack$，$f_{i,j - 1}$ 对应的区间划分设为 $\left\lbrack b_{1},b_{2} - 1 \right\rbrack,\left\lbrack b_{2},b_{3} - 1 \right\rbrack,\ldots\left\lbrack b_{j - 1},i \right\rbrack$。 使用反证法，设 $a_{j} < b_{j - 1}$，则对决策 $a_{j} - 1,j - 1$ 与 $b_{j - 1},j - 1$ 使用 $p_{i,j} \leq p_{i + 1,j}$ 可以得到 $a_{j - 1} < b_{j - 2}$，以此类推可得 $a_{2} < b_{1}$，而 $b_{1} = 1$，矛盾，因此原命题成立。 这种方法的代码如下： ```cpp for(int j=1;j<=m;++j){ p[n+1][j]=n; for(int i=n;i;--i){//逆序循环是因为要使用p(i+1,j) for(int k=p[i][j-1];k<=p[i+1][j];++k) if(dp[k][j-1]+w(k+1,i)<dp[i][j])dp[i][j]=dp[k][j-1]+w(k+1,i),p[i][j]=k; } } ``` 与之前类似地，对于任意 $i - j$ 一致的斜线共有 $O(n)$ 次转移，而 $i - j$ 可能有 $m + n$ 种，因此时间复杂度 $O\left( n(n + m) \right)$。 其实还有更好的办法。 ### 例题 6：[\[IOI2000\] 邮局 加强版](https://www.luogu.com.cn/problem/6246) 在此题中，$n,m \leq 5 \times 10^{5}$。 再再次使用前人的智慧，发现 $w_{n,j}$ 是一个下凸函数（指斜率单调不减），大概长这样：（这个图取自原题目中测试点 2 的数据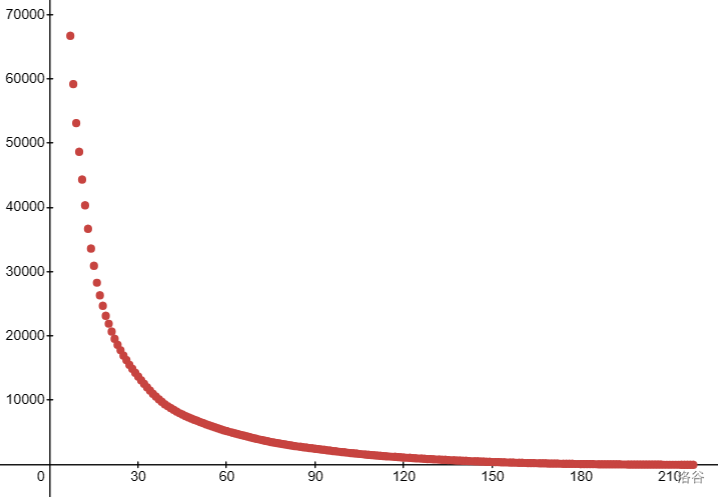）  要证明凸性，只需证明 $f_{n,j - 1} + f_{n,j + 1} \geq 2f_{n,j}$。 同样考虑区间分划，将 $f_{n,j - 1},f_{n,j},f_{n,j + 1}$ 对应的区间划分分别设为\ $\left\lbrack a_{1},a_{2} - 1 \right\rbrack,\left\lbrack a_{2},a_{3} - 1 \right\rbrack,\ldots\ldots\left\lbrack a_{j - 1},n \right\rbrack$\ $\left\lbrack b_{1},b_{2} - 1 \right\rbrack,\left\lbrack b_{2},b_{3} - 1 \right\rbrack,\ldots\ldots\left\lbrack b_{j},n \right\rbrack$\ $\left\lbrack c_{1},c_{2} - 1 \right\rbrack,\left\lbrack c_{2},c_{3} - 1 \right\rbrack,\ldots\ldots\left\lbrack c_{j + 1},n \right\rbrack$ 将 $f_{n,j + 1}$ 对应区间分划中第一个满足 $c_{k} > a_{k - 2}$ 的位置拆出来，交换后半段，形成两个长度为 $j$ 的分划，由于最优性，可以知道这两个划分的代价和不低于 $2f_{n,j}$。 分划如下： $\left\lbrack a_{1},a_{2} - 1 \right\rbrack\ldots\left\lbrack a_{k - 2},c_{k + 1} - 1 \right\rbrack,\left\lbrack c_{k + 1},c_{k + 2} - 1 \right\rbrack,\ldots\left\lbrack c_{j + 1},n \right\rbrack$\ $\left\lbrack c_{1},c_{2} - 1 \right\rbrack\ldots\left\lbrack c_{k},a_{k - 1} - 1 \right\rbrack,\left\lbrack a_{k - 1},a_{k} - 1 \right\rbrack,\ldots\left\lbrack a_{j - 1},n \right\rbrack$\ 对 $a_{k - 2},c_{k},a_{k - 1} - 1,c_{k + 1} - 1$ 应用四边形不等式，得\ $w_{a_{k - 2},a_{k - 1} - 1} + w_{c_{k},c_{k + 1} - 1} \leq w_{a,c_{k + 1} - 1} + w_{c_{k},a_{k + 1} - 1}$\ 即交换后两个分划的代价和不低于 $f_{n,j - 1} + f_{n,j + 1}$，得证。 知道凸性之后，就可以用 wqs 二分解决了。 为了方便，使用原题目中的样例进行演示，它的图像长这样（由于点 $(1,117)$ 过高不放出）： 由于斜率具有单调性，考虑二分斜率。 当枚举到一个斜率 $k$ 时，根据每个点 $\left( j,f_{n,j} \right)$ 与斜率 $k$ 作直线，如当 $k = - 5$ 时长这样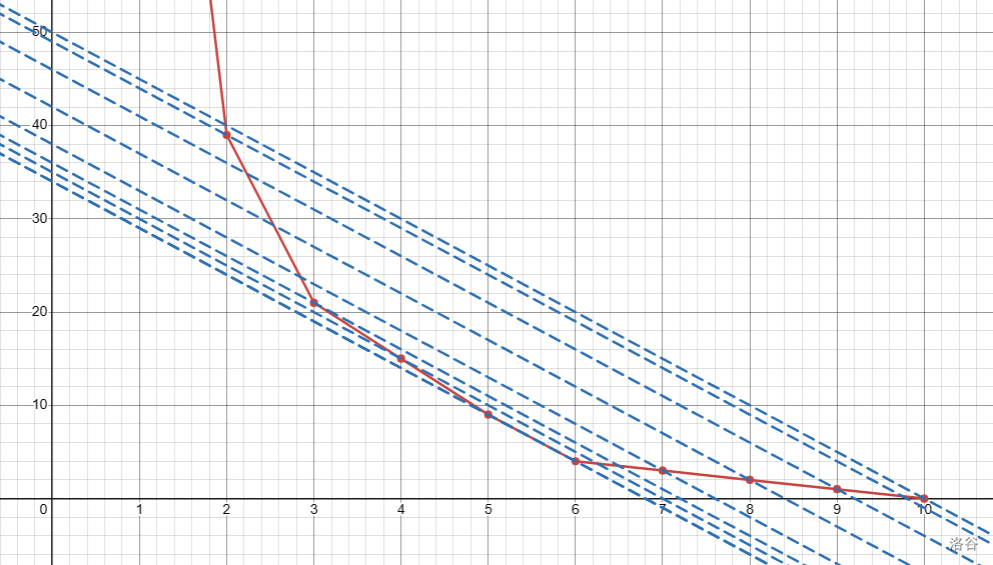： [对应图表](https://www.desmos.com/calculator/cqv46sz5vc?lang=zh-CN) 可以发现，当且仅当一个点作出的直线是最下面的那条（也就是这个点是切点），连接这个点的两条线段的斜率 $k_{1},k_{2}$ 满足 $k_{1} \leq k \leq k_{2}$。 考虑如何快速计算最下面的那条直线。由于斜率相等，尝试从 $b = f_{n,j} - j \ast k$ 入手，$b$ 最小的直线即为所求。 可以发现，要计算这个东西只要将价值函数设为 $w'_{i,j} = w_{i,j} - k$，然后不考虑选 $m$ 个直接用单调队列 + 二分求出所有 $f'_{i} = \min\limits_{k \leq i}\left( f'_{k} + w'_{k,i} \right)$ 即可计算出最小的 $b$，再在过程中记录取到最小的 $b$ 所用的 $j$ 即可。 注意到斜率可能产生平台，比如当 $k = 6$ 时会出现这种情况：  因此，在转移时，要注意只能取到平台的一端，同时注意最终答案的存储。 有两种写法： ```cpp void solve(){//取平台左侧的写法 deque<int> q; l[0]=1,r[0]=n; q.push_back(0); for(int i=1;i<=n;++i){ while(!q.empty()&&i>r[q.front()])q.pop_front(); dp[i]=w(q.front(),i)-Mid,cnt[i]=cnt[q.front()]+1; while(!q.empty()&&w(q.back(),l[q.back()])>=w(i,l[q.back()]))//这里变了 q.pop_back(); if(q.empty()){ q.push_back(i); l[i]=i+1,r[i]=n; } else if(w(q.back(),r[q.back()])<=w(i,r[q.back()])){//这里变了 if(r[q.back()]<n){ q.push_back(i); l[i]=r[q.back()]+1,r[i]=n; } } else{ int L=l[q.back()],R=r[q.back()],mid,p; while(R>=L){ mid=(R+L)/2; if(w(q.back(),mid)>=w(i,mid))p=mid,R=mid-1;//这里变了 else L=mid+1; } r[q.back()]=p-1,l[i]=p,r[i]=n; q.push_back(i); } } } //主函数内二分部分 long long ans,L=-1e14,R=0; while(R>=L){ Mid=(L+R)/2; solve(); if(cnt[n]<=m)ans=dp[n]+m*Mid,L=Mid+1;//当最大点在n左侧时统计答案 else R=Mid-1; } ``` ```cpp void solve(){//取平台右侧的写法 deque<int> q; l[0]=1,r[0]=n; q.push_back(0); for(int i=1;i<=n;++i){ while(!q.empty()&&i>r[q.front()])q.pop_front(); dp[i]=w(q.front(),i)-Mid,cnt[i]=cnt[q.front()]+1;//计算f' while(!q.empty()&&w(q.back(),l[q.back()])>w(i,l[q.back()])) q.pop_back(); if(q.empty()){ q.push_back(i); l[i]=i+1,r[i]=n; } else if(w(q.back(),r[q.back()])<w(i,r[q.back()])){ if(r[q.back()]<n){ q.push_back(i); l[i]=r[q.back()]+1,r[i]=n; } } else{ int L=l[q.back()],R=r[q.back()],mid,p; while(R>=L){ mid=(R+L)/2; if(w(q.back(),mid)>w(i,mid))p=mid,R=mid-1; else L=mid+1; } r[q.back()]=p-1,l[i]=p,r[i]=n; q.push_back(i); } } } //主函数内二分部分 long long ans,L=-1e14,R=0; while(R>=L){ Mid=(L+R)/2; solve(); if(cnt[n]<m)L=Mid+1; else ans=dp[n]+m*Mid,R=Mid-1;//当最大点在n右侧时统计答案 } ``` upd：因为 $f_{n,j}-f_{n,j-1}$，可以直接二分。 习题： - 一维 DP [Yakiniku Restaurants](https://www.luogu.com.cn/problem/AT_arc067_d)\ [\[HNOI2008\] 玩具装箱](https://www.luogu.com.cn/problem/P3195)\ [Max (Sum - Max)](https://www.luogu.com.cn/problem/AT_abc348_g)\ [\[COCI 2023/2024 #5\] Rolete](https://www.luogu.com.cn/problem/P10260)\ [「雅礼集训 2017 Day5」珠宝 /「NAIPC2016」Jewel Thief](https://loj.ac/p/6039) - 二维 DP - 区间 DP [\[NOI1995\] 石子合并](https://www.luogu.com.cn/problem/P1880)\ [\[IOI1998\] Polygon](https://www.luogu.com.cn/problem/P4342) - 区间拆分 [Ciel and Gondolas](https://www.luogu.com.cn/problem/CF321E)\ [\[CmdOI2019\] 任务分配问题](https://www.luogu.com.cn/problem/P5574)\ [忘情](https://www.luogu.com.cn/problem/P4983) - 所有的单调队列 / 斜率优化题目