线性代数学习笔记

## 前言

### 更新日志

2025.04.30 更新了 1.1 二阶行列式。

2025.05.01 更新了 1.2 三阶行列式 $\sim$ 1.5 行列式的性质。

## 1.1 二阶行列式

### 基本概念

二阶行列式的定义：由二行二列四个元素所组成的算式，记作：

$\begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}$

二阶行列式的值：主对角线乘积加上次对角线乘积的相反数（是两项相加），即 $a_{1,1}a_{2,2} + (-a_{1,2}a_{2,1})$，例如：

$\begin{bmatrix} 2 & 4 \\ 1 & 3 \end{bmatrix} = 2 \times 3 - 1 \times 4=2$

二、三阶行列式对角线法则：主对角线为正，次对角线为负。

对于所有的行列式，每一项都是由不同行不同列的值得来。

**没有行列数目不同的行列式。**

### 代数意义

求解二元线性方程组。

$$
\begin{cases}
a_{1,1}x_1+a_{1,2}x_2=b_1 \\
a_{2,1}x_1+a_{2,2}x_2=b_2 \\
\end{cases}
$$

对于上述方程组：

例如先消 $x_2$，变形得：

$$
\begin{cases}
a_{1,1}a_{2,2}x_1+a_{1,2}a_{2,2}x_2=a_{2,2}b_1 \\
a_{1,2}a_{2,1}x_1+a_{1,2}a_{2,2}x_2=a_{1,2}b_2 \\
\end{cases}
$$

相减得：

$(a_{1,1}a_{2,2}-a_{1,2}a_{2,1})x_1=a_{2,2}b_1-a_{1,2}b_2$

所以（如果 $a_{1,1}a_{2,2}\ne a_{1,2}a_{2,1}$）：

$x_1=\frac{a_{2,2}b_1-a_{1,2}b_2}{a_{1,1}a_{2,2}-a_{1,2}a_{2,1}}=\frac{\begin{bmatrix} b_1 & a_{1,2} \\ b_2 & a_{2,2} \end{bmatrix}}{\begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}}$

同理可得：

$x_2=\frac{\begin{bmatrix} a_{2,1} & b_1 \\ a_{2,1} & b_2 \end{bmatrix}}{\begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}}$

定义系数行列式：

$D=\begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}$

同时定义：

$D_1=\begin{bmatrix} b_1 & a_{1,2} \\ b_2 & a_{2,2} \end{bmatrix}$

$D_2=\begin{bmatrix} a_{2,1} & b_1 \\ a_{2,1} & b_2 \end{bmatrix}$

所以，当 $D \ne 0$ 时：

有且仅有一个解。

$$
\begin{cases}
x_1=\frac{D_1}{D} \\
x_2=\frac{D_2}{D} \\
\end{cases}
$$

以上被称为克拉默法则。

当 $D=0$ 时：

如果两方程矛盾，无解。

否则有无穷多个解。

### 几何意义

代表二维空间中平行四边形的面积。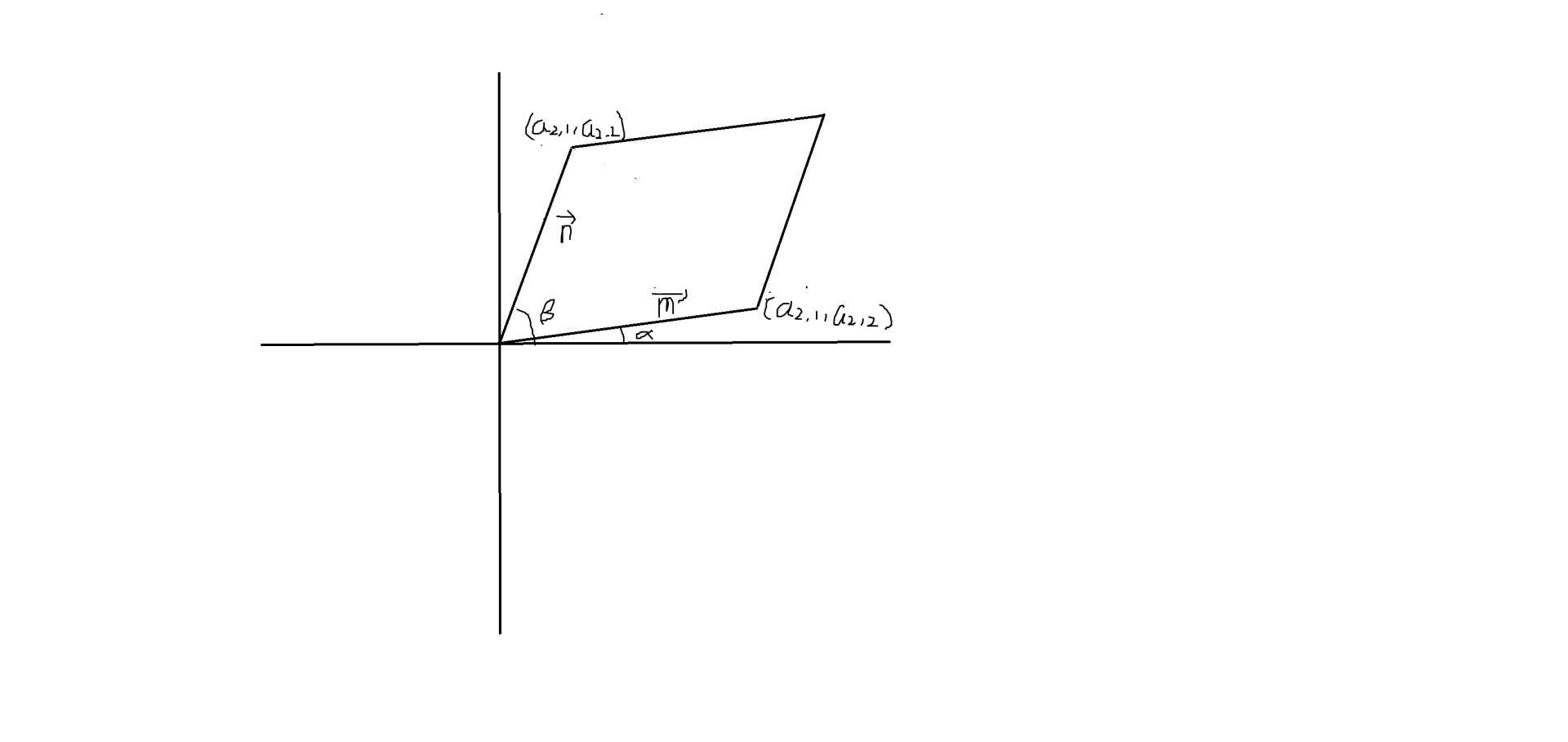

![](https://cdn.luogu.com.cn/upload/image_hosting/ocouqphk.png)

令 $x$ 表示向量 $m$ 的模长，$y$ 表示向量 $n$ 的模长。

$$
\begin{align*}
S &= ah \\
&=xy\cdot \sin(\beta-\alpha) \\
&=xy(\sin \beta \cos \alpha - \sin  \alpha \cos \beta) \\
&= x \cos \alpha \cdot y \sin \beta - x \sin \alpha \cdot y \cos \beta \\
&= a_{1,1}a_{2,2}-a_{1,2}a_{2,1} \\
&=\begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}\\
\end{align*}
$$

## 1.2 三阶行列式

### 基本概念

三阶行列式的定义：由三行三列九个元素所组成的算式，记作：

$\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\\end{bmatrix}$

三阶行列式的值为（画心形）：

$a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}+(-a_{1,3}a_{2,2}a_{3,1})+(-a_{1,2}a_{2,3}a_{3,1})+(-a_{1,1}a_{2,3}a_{3,2})$

### 代数意义

求解三元线性方程组。

$$
\begin{cases}
a_{1,1}x_1+a_{1,2}x_2+a_{1,3}x_3=b_1 \\
a_{2,1}x_1+a_{2,2}x_2+a_{2,3}x_3=b_2 \\
a_{3,1}x_1+a_{3,2}x_2+a_{3,3}x_3=b_3 \\
\end{cases}
$$

例：

$$
\begin{cases}
x-y-z=2 \\
2x-y-3z=1 \\
3x+2y-5z=0 \\
\end{cases}
$$

系数行列式：

$D=\begin{bmatrix} 1 & -1 & -1 \\ 2 & -1 & 3 \\ 3 & 2 & -5 \end{bmatrix}=3$

$D_x$ 就是将 $D$ 的第 $x$ 列全部替换成 $b_1,b_2,b_3$，在本例中是 $2,1,0$。

得：

$$
\begin{cases}
x=\frac{D_1}{D}=5 \\
y=\frac{D_2}{D}=0 \\
z=\frac{D_3}{D}=3 \\ 
\end{cases}
$$

### 几何意义

三维空间中平行六面体的体积。

即以三个空间向量的混合积。

扩展：$x$ 阶行列式的几何意义就是 $x$ 维空间中平行 $2x$ 面体的“体积”。

## 1.3 排列和对换

### 排列

排列：由 $n$ 个数 $1 \sim n$ 组成的一个有序数组为一个 $n$ 级排列。

顺序：前小后大为顺序。

逆序：前大后小为逆序。

一个逆序：一对逆序的数字。

逆序数：一个排列的逆序的总数。

奇排列：一个排列的逆序数为奇数。

偶排列：一个排列的逆序数为偶数。

标准（自然）排列：逆序数为 $0$ 的排列。

如果一个排列 $p_1,p_2,…,p_n$ 的逆序数为 $k$，那么排列 $p_n,p_{n-1},…,p_1$ 的逆序数为 $\frac{n(n-1)}{2}-k$。

### 对换

对换：排列中的任意两个数交换位置，其余不变。

相邻对换：排列中的相邻两个数交换位置，其余不变。

排列经过一次对换，奇偶性改变。

## 1.4 高阶行列式

$n$ 阶行列式的定义：由 $n$ 行 $n$ 列 $n^2$ 个元素所组成的算式。

按行定义：

$D= \begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}=\sum (-1)^{t(p)} \Pi_{i=1}^n a_{i,p_i}$

其中 $t(p)$ 表示排列 $p$ 的奇偶性。

按列定义：

其中 $t(p)$ 表示排列 $p$ 的奇偶性。

一般定义：

$D= \begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}=\sum (-1)^{t(a)+t(b)} \Pi_{i=1}^n a_{a_i,b_i}$

其中 $t(a),t(b)$ 分别表示排列 $a,b$ 的奇偶性。

## 1.5 行列式的性质

**行和列地位相同。**

转置行列式：

如 $D= \begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}$ 的转置行列式 $D^T= \begin {bmatrix} a_{1,1} & a_{2,1} & … & a_{n,1} \\ a_{1,2} & a_{2,2} & … & a_{n,2} \\
… & … & & … \\
a_{1,n} & a_{2,n} & … & a_{n,n} \\
\end{bmatrix}$

1. 行列互换，其值不变，即 $D=D^T$。

2. 对换行列式中的两行，其余不变，行列式变号。

3. 若行列式某一行有公因子 $k$，那么 $k$ 可以提出，即：

$\begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ k \cdot a_{2,1} & k \cdot a_{2,2} & … & k \cdot a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}= k \cdot \begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}$

4. 行列式中若有两行成比例，则行列式的值为 $0$。

5. 行列式中如果有一行都是两个数相加的形式，那么这个行列式可以表示为两个行列式相加，即：

$\begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ b_{2,1} + a_{2,1} & b_{2,2} + a_{2,2} & … & b_{2,n} + a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}= \begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}+\begin {bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ b_{2,1} & b_{2,2} & … & b_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}$

6. 将行列式的某一行元素全部乘上一个系数 $k$，并加到某一行上，所得新行列式的值等于原行列式的值，例：

$\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\\end{bmatrix}=\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ k \cdot a_{1,1}+a_{3,1} & k \cdot a_{1,2}+a_{3,2} & k \cdot a_{1,3}+a_{3,3} \\\end{bmatrix}$

对于第四条，乘法结合律易证。

对于第五条，分配律易证。

对于第六条，拆开后结合第四、五条易证。

## 1.6 行列式的计算

### 特殊行列式

1. $\begin{bmatrix} a_{1,1} & 0 & … & 0 \\ 0 & a_{2,2} & … & 0 \\
… & … & & … \\
0 & 0 & … & a_{n,n} \\
\end{bmatrix}=\Pi_{i=1}^n a_{i,i}$

2. $\begin{bmatrix} a_{1,1} & 0 & … & 0 \\ a_{2,1} & a_{2,2} & … & 0 \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}=\Pi_{i=1}^n a_{i,i}$

3. $\begin{bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ 0 & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
0 & 0 & … & a_{n,n} \\
\end{bmatrix}=\Pi_{i=1}^n a_{i,i}$

4. $\begin{bmatrix} 0 & 0 & … & a_{1,n} \\
… & … & & … \\
0 & a_{n-1,2} & … & 0\\
a_{n,1} & 0 & … & 0 \\
\end{bmatrix}=(-1)^{\frac{n(n-1)}{2}}\Pi_{i=1}^n a_{i,i}$

5. $\begin{bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} & 0 & … & 0 & 0 \\
a_{2,1} & a_{2,2} & … & a_{2,n} & 0 & …& 0 & 0 \\
… & … & & … & … & & … & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} & 0 & … & 0 & 0 \\
0 & 0 & … & 0 & a_{n+1,n+1} & … & a_{n+1,2n-1} & a_{n+1,2n} \\
… & … & & … & … & & … & … \\
0 & 0 & … & 0 & a_{2n-1,n+1} & … & a_{2n-1,2n-1} & a_{2n-1,2n} \\
0 & 0 & … & 0 & a_{2n,n+1} & … & a_{2n,2n-1} & a_{2n,2n} \\
\end{bmatrix}=\begin{bmatrix} a_{1,1} & a_{1,2} & … & a_{1,n} \\ a_{2,1} & a_{2,2} & … & a_{2,n} \\
… & … & & … \\
a_{n,1} & a_{n,2} & … & a_{n,n} \\
\end{bmatrix}\begin{bmatrix} a_{n+1,n+1} & a_{n+1,n+2} & … & a_{n+1,2n} \\ a_{n+2,n+1} & a_{n+2,n+2} & … & a_{n+2,2n} \\
… & … & & … \\
a_{2n,n+1} & a_{2n,n+2} & … & a_{2n,2n} \\
\end{bmatrix}$

对于第二个式子的说明：

我们只考虑结果不为 $0$ 的项。

可以发现，第一行只能取 $a_{1,1}$，由于都是由不同行不同列的值得来，所以第二行只能取 $a_{2,2}$，以此类推可得。

第三个式子与第二个同理。

第二个被称为下三角行列式，第三个被称为上三角行列式。

对于第五个式子，根据乘法原理可得。

### 基本行列式

例 $1$. 求行列式 $D=\begin{bmatrix} 3 & 1 & -1 & 2 \\ -5 & 1 & 3 & -4 \\
2 & 0 & 1 & -1 \\
1 & -5 & 3 & -3 \\
\end{bmatrix}$ 的值。

尝试将行列式转化为上三角行列式。

解：

$$
\begin{align*}
\text{原式} &= -\begin{bmatrix} 1 & 3 & -1 & 2 \\ 1 & -5 & 3 & -4 \\
0 & 2 & 1 & -1 \\
-5 & 1 & 3 & -3 \\
\end{bmatrix} \\
&= -\begin{bmatrix} 1 & 3 & -1 & 2 \\ 0 & -8 & 4 & -6 \\
0 & 2 & 1 & -1 \\
-5 & 1 & 3 & -3 \\
\end{bmatrix} \\
&= -\begin{bmatrix} 1 & 3 & -1 & 2 \\ 0 & -8 & 4 & -6 \\
0 & 2 & 1 & -1 \\
0 & 16 & -2 & 7 \\
\end{bmatrix} \\
&= \begin{bmatrix} 1 & 3 & -1 & 2 \\ 0 & 2 & 1 & -1 \\ 0 & -8 & 4 & -6 \\
0 & 16 & -2 & 7 \\
\end{bmatrix} \\
&= \begin{bmatrix} 1 & 3 & -1 & 2 \\ 0 & 2 & 1 & -1 \\ 0 & 0 & 8 & -10 \\
0 & 0 & -10 & 15 \\
\end{bmatrix} \\
&= \begin{bmatrix} 1 & 3 & -1 & 2 \\ 0 & 2 & 1 & -1 \\ 0 & 0 & 8 & -10 \\
0 & 0 & 0 & \frac{5}{2} \\
\end{bmatrix} \\
&= 1 \times 2 \times 8 \times \frac{5}{2} \\
&= 40
\end{align*}
$$

例 $2$. 求行列式 $D=\begin{bmatrix} a & b & c & d \\ a & a+b & a+b+c & a+b+c+d \\
a & 2a+b & 3a+2b+c & 4a+3b+2c+d \\
a & 3a+b & 6a+3b+c & 10a+6b+3c+d \\
\end{bmatrix}$ 的值。

沿用刚才的思路即可。

解：

$$
\begin{align*}
\text{原式} &= \begin{bmatrix} a & b & c & d \\ 0 & a & a+b & a+b+c \\
0 & a & 2a+b & 3a+2b+c \\
0 & a & 3a+b & 6a+3b+c \\
\end{bmatrix} \\
&= \begin{bmatrix} a & b & c & d \\ 0 & a & a+b & a+b+c \\
0 & 0 & a & 2a+b \\
0 & 0 & a & 3a+b \\
\end{bmatrix} \\
&= \begin{bmatrix} a & b & c & d \\ 0 & a & a+b & a+b+c \\
0 & 0 & a & 2a+b \\
0 & 0 & 0 & a \\
\end{bmatrix} \\
&= a^4
\end{align*}
$$

### 行、列和相等行列式

例 $3$. 求行列式 $D=\begin{bmatrix} 3 & 1 & 1 & 1 \\ 1 & 3 & 1 & 1 \\
1 & 1 & 3 & 1 \\
1 & 1 & 1 & 3 \\
\end{bmatrix}$ 的值。

这是一个行、列和相等的行列式。

可以将第 $2,3,4$ 行加上去，提出公因子后再用第一行去减。

$$
\begin{align*}
\text{原式} &= 6 \times \begin{bmatrix} 1 & 1 & 1 & 1 \\
1 & 3 & 1 & 1 \\
1 & 1 & 3 & 1 \\
1 & 1 & 1 & 3 \\
\end{bmatrix} \\
&= 6 \times \begin{bmatrix} 1 & 1 & 1 & 1 \\
0 & 2 & 0 & 0 \\
0 & 0 & 2 & 0 \\
0 & 0 & 0 & 2 \\
\end{bmatrix} \\
&= 6 \times 2^3 \\
&= 48
\end{align*}
$$

例 $4$. 求行列式 $D= \begin {bmatrix} x & y & y & … & y \\ y & x & y & … & y \\
y & y & x & … & y \\
… & … & … & & … \\
y & y & y & … & x \\
\end{bmatrix}$ 的值。

这也是一个行、列和相等的行列式，沿用刚才的思路即可。

$$
\begin{align*}
\text{原式} &= [x+(n-1)y] \begin {bmatrix} 1 & 1 & 1 & … & 1 \\ y & x & y & … & y \\
y & y & x & … & y \\
… & … & … & & … \\
y & y & y & … & x \\
\end{bmatrix} \\
&= [x+(n-1)y]
\begin {bmatrix} 1 & 1 & 1 & … & 1 \\ 0 & x - y & 0 & … & 0 \\
0 & 0 & x-y & … & 0 \\
… & … & … & & … \\
0 & 0 & 0 & … & x-y \\
\end{bmatrix} \\
&= (x-y)^{n-1}(ny+x-y)
\end{align*}
$$

例 $5$. 求行列式 $D= \begin {bmatrix} x & a_1 & a_2 & … & a_n \\ a_1 & x & a_2 & … & a_n \\
a_1 & a_2 & x & … & a_n \\
… & … & … & & … \\
a_1 & a_2 & a_3 & … & x \\
\end{bmatrix}$ 的值。

这是一个行和相等行列式，原理相同。

$$
\begin{align*}
\text{原式} &= 
(x+\sum_{i=1}^n a_i)\begin {bmatrix} 1 & a_1 & a_2 & … & a_n \\ 1 & x & a_2 & … & a_n \\
1 & a_2 & x & … & a_n \\
… & … & … & & … \\
1 & a_2 & a_3 & … & x \\
\end{bmatrix} \\
&= (x+\sum_{i=1}^n a_i)\begin {bmatrix} 1 & 0 & 0 & … & 0 \\ 1 & x-a_1 & 0 & … & 0 \\
1 & a_2-a_1 & x-a_2 & … & 0 \\
… & … & … & & … \\
1 & a_2-a_1 & a_3-a_2 & … & x-a_n \\
\end{bmatrix} \\
&= (x+\sum_{i=1}^n a_i) \cdot \Pi_{i=1}^n(x-a_i)
\end{align*}
$$

### 爪形行列式

例 $6$. 求行列式 $D= \begin {bmatrix} 1 & a_1 & a_2 & … & a_n \\ a_2 & 1 & 0 & … & 0 \\
a_3 & 0 & 1 & … & 0 \\
… & … & … & & … \\
a_1 & 0 & 0 & … & 1 \\
\end{bmatrix}$ 的值。

这是一个爪型行列式，直接暴力计算十分麻烦。

尝试用斜爪消去平爪。

因为第 $2$ 行后面一大串全部都是 $0$，乘以任意数加上去都没有影响，然后平爪全变成了 $0$，整体变成下三角行列式。

解：

$$
\begin{align*}
\text{原式} &= 
\begin {bmatrix} 1-a_1^2 & 0 & a_2 & … & a_n \\ a_2 & 1 & 0 & … & 0 \\
a_3 & 0 & 1 & … & 0 \\
… & … & … & & … \\
a_1 & 0 & 0 & … & 1 \\
\end{bmatrix} \\
&= \begin {bmatrix} 1-\sum_{i=1}^n a_i^2 & 0 & 0 & … & 0 \\ a_2 & 1 & 0 & … & 0 \\
a_3 & 0 & 1 & … & 0 \\
… & … & … & & … \\
a_1 & 0 & 0 & … & 1 \\
\end{bmatrix} \\
&= 1-\sum_{i=1}^n a_i^2
\end{align*}
$$

例 $7$. 求行列式 $D= \begin {bmatrix} a_1 & 0 & 0 & … & 0 & c_1 \\ 0 & a_2 & 0 & … & 0 & c_2 \\
0 & 0 & a_3 & … & 0 & c_3 \\
… & … & … & & … & …\\
0 & 0 & 0 & … & a_n & c_n \\
b_1 & b_2 & b_3 & … & b_n & a_{n+1} \\
\end{bmatrix}$ 的值。

这是一个爪型行列式，还是按之前的方法。

$$
\begin{align*}
\text{原式} &= \begin {bmatrix} a_1 & 0 & 0 & … & 0 & 0 \\ 0 & a_2 & 0 & … & 0 & 0 \\
0 & 0 & a_3 & … & 0 & 0 \\
… & … & … & & … & …\\
0 & 0 & 0 & … & a_n & 0 \\
b_1 & b_2 & b_3 & … & b_n & a_{n+1}-\sum_{i=1}^n\frac{b_i \cdot c_i}{a_i} \\
\end{bmatrix} \\
&= (\Pi_{i=1}^n a_i)(a_{n+1}-\sum_{i=1}^n\frac{b_i \cdot c_i}{a_i})
\end{align*} 
$$