【笔寄】RMQ - 洛谷保存站

## 目录

1. 简介

2. 浅析倍增

3. $ST$表算法

4. 题目

4.1. 1615 -- 【RMQ练习】奶牛排队（USACO 2007 January Gold）2591

## $1$ 简介

RMQ问题($Range\space Mininum/Maxinum\space Query$)，就是求一系列区间的最大/最小值(静态)，我们应该首选ST表算法，但在此之前，我们应该了解倍增算法

## $2$ 浅析倍增

倍增，其实就是将一个个小段化成长度为$2^k$的区间(或是以$2^k$的长度搜寻)，为甚么是$2$的幂次呢?本人不才，无法解释qwq

## $3$ $ST$表

我们先定义一个数组$STMax_{i,j}$为从i到j的最大值，虽然无论从空间，还是时间上来说都不可以，但在这里我还是要讲一下它的递推式是

$$
STMax_{i,j}=\left\{ \begin{array}{c} \max(STMax_{i,j-1},a_j) & {i < j}\\ a_i & {i = j}\\ \end{array} \right.
$$

我们发现$\max(STMax_{i,j-1},a_j)$中的$a_j$感觉不划算，于是很多人就放弃了

然而，某位神人发现如果将$a_j$替换成一个在$STMax$列表的数，那该多好呀

那位神人立即想到了倍增，写出了以下递推式：

$$
STMax_{i,i+2^k-1} = \left\{ \begin{array}{c} \max(STMax_{i,i+2^{k-1}-1},STMax_{i+2^{k-1},(i+2^{k-1})+2^{k-1}-1})& i < j\\ a_i & i = j \end{array} \right. 
$$

然后他发现空间复杂度上是吃不消的，他又发现式子中存在形如$xxx+2^{xxx}-1$的形式的式子，于是他改变了定义

$STMax_{i,j}$为从$i$到$i + 2^j - 1$的最大值

那么递推式就是：

$$
STMax_{i,k} = \left\{ \begin{array}{c} \max(STMax_{i,k-1},STMax_{i+2^{k-1},k-1})& k \geqslant 0 \\ a_i & k=0 \end{array} \right.
$$

这就是今天的ST表算法

代码($a$数组从$1$开始存)：

```cpp
int a[MAXN];
int STMax[MAXN][MAXLogn];
int my_log[MAXN];//存以2为底的log
int main() {
    int n;
	//lots of scan...
	my_log[0] = -1;
	for (int i = 1; i <= n; i++) {
		my_log[i] = my_log[i / 2] + 1;
	}
	for (int i = 1; i <= n; i++) STMax[i][0] = a[i];
	for (int j = 1; j <= my_log[n]; j++) {
		for (int i = 1; i + (1 << j) - 1 <= n; i++) {
			STMax[i][j] = max(STMax[i][k - 1], STMax[i + (1 << k - 1)][k - 1];
		}
	}
}
```

但是到现在，我们还没讲查询，其实查询特别简单，一个图就可以明白：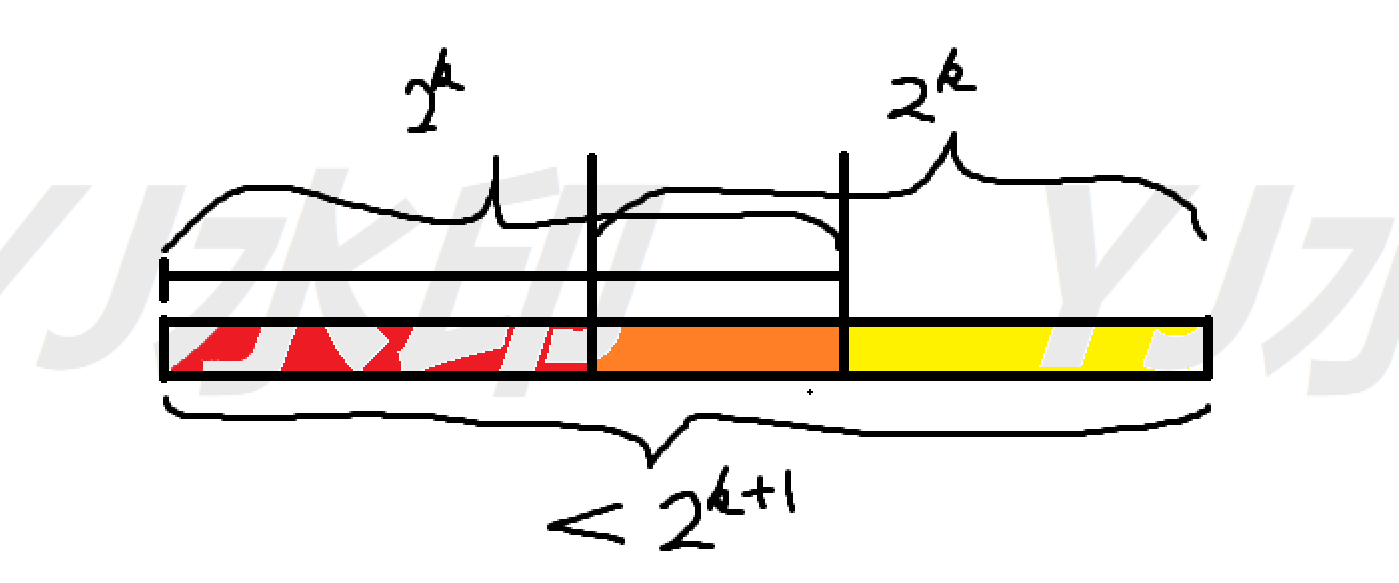

![JPmL01.png](https://s1.ax1x.com/2020/04/15/JPmL01.png)

代码：

```cpp
int jump = my_log[r - l + 1];
printf("%d", max(STMax[i][jump], STMax[j - (1 << jump) + 1][jump]));
```

## $4$ 例题

### $4.1$ 1615 -- 【RMQ练习】奶牛排队（USACO 2007 January Gold）2591

#### Description

> 在每天挤奶的时候，农民约翰的N头牛（1≤n≤50000）总是排成一列。有一天，约翰决定与他的牛们一起玩一个极限飞盘游戏。为了简单起见，他将从奶牛队列里面选一定范围内的奶牛来玩这个游戏。然而所有的牛对这个游戏都很感兴趣。农民约翰列出了Q份名单（1≤Q≤200000）和每个奶牛的高度（1≤高度≤1000000）。对于每一份名单，他想你帮助他确定在每份名单中高度最高的奶牛与高度最低的奶牛的高度差是多少。

#### Solution

裸的，存最大值和最小值即可

#### code

```cpp
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 50002;
const int MAXLogn = 20;
int my_log[MAXN];
int STMax[MAXN][MAXLogn];
int STMin[MAXN][MAXLogn];
int a[MAXN];
int main() {
	my_log[0] = -1;
	int n, m;
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		STMax[i][0] = STMin[i][0] = a[i];
		my_log[i] = my_log[i / 2] + 1;//qwq
	}
	for (int i = 1; i <= my_log[n]; i++) {
		for (int j = 1; j <= n - (1 << i) + 1; j++) {
			STMin[j][i] = min(STMin[j][i - 1], STMin[j + (1 << i - 1)][i - 1]);
			STMax[j][i] = max(STMax[j][i - 1], STMax[j + (1 << i - 1)][i - 1]);
		}
	}
	for (int i = 0; i < m; i++) {
		int l, r;
		scanf("%d %d", &l, &r);
		int jump = my_log[r - l + 1];
		printf("%d\n", max(STMax[l][jump], STMax[r - (1 << jump) + 1][jump]) - min(STMin[l][jump], STMin[r - (1 << jump) + 1][jump]));
	}
	return 0;
}
```

正在渲染内容...