比赛总结专栏
25.8.28 比赛总结
没有话就把嘴巴一闭。
唯一的败笔出现在 T3,关于一个正确性没什么保障的歪解上。作为歪解,而且数据范围越大错误率越高的歪解,正常来说应该优先考虑尽可能提升正确的概率,而不是扩大可以支持的范围上。实测适当扩大范围可以多拿 25pts。
当然了,题面里面也完全没有说这道题要开捆绑测试。因此上面的决策也并非不可理解,毕竟大样例都能过的正确率一般不会太低。
别的话,无论是算法上,还是决策上,再无纰漏。心态上略有问题,不过无伤大雅。
25.8.27 比赛总结
好事轮不到我,坏事一直抡我 :(。
给看了一眼 QMR 的总结,综合一下这三天 RK1 三次易主的情况,说一点我的看法:
首先,这三天以来,抛开第二天不谈吧,单论算法上讲确实我是没有出什么大的问题的,但是为什么没能坐住第三天的 RK1?
- 细节决定成败。一个不算空间的的坏习惯就是 100pts 的血淋淋的代价。人叫人百教不听,事教人一次就会。这种能拿分却没拿到分的情况,不允许第二次。
- 心态。别的暂且不说,第二天真的完全没有拿 RK1 的希望吗?完全是有的。T3 距离那“因为少半个小时”挂掉的 40pts 犯的唯一一个错是三带二必须带对子。当时因为少了半个小时心理极度不平衡,没有及时调整心态,最后受影响的 1h 内个人感觉都是带有明显的情绪的。考场上无论发生什么,一定不能慌了心态。
- 习惯。习惯是很可怕的,好的习惯是能救你一命的。比如说 MLE,文件读写出错,调试没删干净等等错误应该在考试最后 10~15 分钟留一点时间,进行最后检查是可以检查出来的。我衷心认为最后留时间检查是一个好办法,但是比如这次考试暴露出来的问题就是一个极其重要的补丁。这种习惯、经验,我认为值得花一点时间相互交流一下。
其次呢,我想分析一下 QMR 和 HJM 能分别得一次 RK1 的原因。毕竟了解不多,但是还是值得略略解析一下的。
新初二的 QMR 给人的感觉就是十万个为什么。爱问问题,而且是沉稳踏实型的,这一点自佩不如,是值得学习的。
新初三的 HJM 了解的就极其少了,但是从今天的分数构成来看,特点就是稳。该拿的分拿了,该骗的分甚至骗的比我略多。这一点在信竞弱省不失为一个显著的优势。
总体来说,一个字:稳。一个是学习的时候稳,一个是考试的时候稳。由衷的表示厉害!向你们学习!
但是我也想说一些问题,从 QMR 的反思中窥见一点:
- 隐私。我并不认为成绩表这种东西是可以直接作为公开总结的一部分光明正大的出现在总结中的。保护隐私也是在网上非常重要的一件事。而且未必所有人愿意你这样子干,略无边界感。
- 务实。邓某曾经说过“没有话就把嘴巴一闭”。总结重在整理经验,修正习惯,查漏补缺,要做到重点突出。像成绩,赛时经过这一类东西应当靠边,非必要甚至可以不出现。同样的话,送给死命模仿 QMR 的 JCY,以及不够正经的,不够务实的新高一信竞队所有人。
JCY@15:47: 哇我写这玩意写了一个小时。
好意思吗?算法上未必,不过这个方向仔细一想,反正我是有点虚的。
别的我也不多说了,尊重个人意愿。下面是我关于本场比赛本身的总结。
T1 写了大大的正解,然后因为没有滚动数组当场 MLE 成 $0$ 分。
好好翻一下之前的比赛总结!这类问题之前总结过,而且至少出现了两次。
当你发现不同寻常的空间限制,尤其是在 $256MB$ 以下的时候务必注意空间是否超出限制,不确定的可以开任务管理器看一看。
考试是甚至没有想过复核一下。以后检查的时候加一个流程:分析时间空间消耗。
T2 没什么说的,分配的时间比较的少,没有什么思路或者突破口,可能也真的说不了什么,题解大致一看是看不懂的,也就是考思维。这个只能考虑多做一做 CF,USACO 等的题了。
不过招笑的是自己花了大把的时间敲对的神秘 DP 对应的 20pts 被自己不检查暴力挂掉的 20pts 抹平了。细节决定成败。
T3 没什么说的,$1h$ 整敲过的中模拟。
T4 磕的时间是最长的,将近两个小时了,反正骗到了该骗的所有分,暂时先不多说什么了,等解法相关总结。
第一个算法相关问题:学死了。看到稍微复杂一点的树链查询就直接上树剖了,可是实际上就像前天的那道题,只要树不动就可以考虑时间上更优的,思维上更简单的倍增。
第二个算法相关问题:维护技巧。体现在代码上不易直接合并的东西可以通过多记录信息,利用类矩阵乘法等强制维护。考场上甚至已经打出了类矩阵乘法的板子,但是边界条件仍然在手动处理,最终逻辑过于复杂而放弃。
第三个算法相关问题:学死了,而且死都没死明白。矩阵乘法一般只会用来优化重复的递推性质的问题。也就是说矩阵乘法只是递推关系的一种直观体现而非方法,根基仍然是转移关系。
总的说出在策略上的问题就是对空间消耗的忽略。算法上的就是学死了,简单问题复杂化,然后死也死不明白。
另外思维上讲,T4 可能确实比 T2 简单?
25.8.26 比赛总结
看解法前,按照难度与相应的时间分配进行初步分析,唯一的问题是因为样例出锅少了 30min,所以凭啥我自己受着呢?
修正分数:100+64+70+55=289pts。
T1 没有出任何岔子。快速解决走人了。
T3 因为 T4 的锅,只留下来了 20min,能尽可能地骗到 30pts 已经挺好的了。
T4 一遍写过想写的所有部分分,然后因为出锅的样例挂掉 30min。
唯一一点值得指摘的也就是 T2 了。
考试时没有经过深度思考就断然放弃了正难则反的方向,然后成功的浪费了我 1h 并且多得了 0pts,只得抓紧时间写暴力走人了。
这道题目的突破口是超过一半的主要食材最多一个。如果能够抓到这个细节,显然会好做很多。
然后就是比较常见的一个 $O(mn^3)$ 的 DP,不够通过,加上数学公式转化,或者仅计算差值等等降维技巧就少一个 $n$,可以过了。
25.8.25 比赛总结
T1 没出什么大的问题,毕竟曾经是郭老带着做了加强版。弱化的就直接弱化处理吧,难度到不了绿。
T2 可惜了,败也细节。整体的思路框架没有出任何问题,贪心的思路也是完全正确的,但是实现的时候却在一个特定的细节坠机了。
比较容易忽略地,我们发现一个较小的数字可能会选择次大值而不一定是最大值,从而将回传到上一层的最大值最大化。
这一点其实可以通过使用 lower_bound 代替双指针直接规避掉,但是优先数量的核心思路骑到头上了(悲),甚至还骑得有问题。
T3 其实算半个动态 DP 的板子题吧,只不过没有动起来。
动态 DP 学的还是太死了,写了一个神秘的 {min,+} 广义矩阵乘法,然后一点正确性没有。当时也只是想写一下 A 部分分,毕竟带修序列动规问题似乎写这个很合理。我想问题在于对动态 DP 远远不够熟悉吧。
T4 什么神秘的结论题?!CCF 出这玩意是想要飞起来吧?
比较大的问题是没有尝试打表找规律。最核心的规律就是在一定的范围内 $V_{n,m+1}=3\times V_{n,m}$。
事实上如果能够注意到这个规律,就能够快速的理解为什么部分分当中会出现关键的 $8\times8$ 的部分分,或者说这个提示性本身已经很强了,但是没有引起足够的注意?遇到这种不明所以的题,还是打打表吧。
25.8.22 比赛总结
没人觉得 T1 一个不知道算不算裸的二分简单题做不出来很诡异吗?没人觉得一个显然错误的贪心轻轻松松拿 60pts 更诡异吗?
总之就是不要轻易抛弃一些简单的算法。他们往往是解前两道题的关键。
考场上随便胡了一个神秘的在 trie 树上面进行伪多源双端队列 bfs 的诡异的做法,然后发现确实能骗到 80pts,但是是随机数据下,理论上可以卡到 60pts 左右。
T2 正解的大方向其实都差不多是知道的,只不过没有往 prim 方向去想。
这种题大多是去找 kruskal 和 prim 在特定情况下的优化的。boruvka 见的还是非常少的,主要是遇到可以批量取出最短边时才会去考虑使用。
T3 正解的第一部拆分贡献其实是相对比较好想的,难就难在统计仅经过一次特定类别的边的路径计数。
题解使用了虚树,效果拔群。考场上思考了一下线段树分支行不行,然后时间复杂度不是很对的样子。
T4 理论时间复杂度是对的,但是常数大到飞起来,跑不过 n^2 暴力。
正解是一个神秘的拼好题,核心思路就是找出两种时间复杂度不同,面对对象不同的部分解法,然后均衡一下时间复杂度拼在一起。
这类思路比较常见,但是考试时没有想到两种思路,只是死命的优化一个思路。然后整出了跑不过 $n^2$ 的 $n\sqrt n\log n$。
25.8.20 比赛总结
有之前某场 htoj 的提高组模拟赛的那个意思:前三道题写飞快,最后一道题完全没思路。没暴露出来什么特别重要的问题。
唯一的教训出在 T1 吧:让实践凌驾于理论之上。
事实上,发现没能通过时去检查代码逻辑很快就发现了问题:强制经过当前连向的点。
理论上来说当时是有机会发现这个问题的:我吸取上一场比赛的教训,仔细思考细节和一些边界条件,比如说完全没有可变轨道。
直觉告诉我可能会出问题,于是没有检查代码的逻辑,而是手搓了一组数据,发现代码能够通过就没有去管了。
同时仔细去回想的话也能发现平时做题的时候有类似的毛病,尤其是出在数学题和 DP 题目的边界条件,转移条件上。
有一些没推的特别清楚的地方,第一反应不是继续思考下去,而是抱着试一试的心态先敲一份出来,不对再去调整。
这样的代价就是“赌上所有”:不调,或者一直调。没有清晰而正确的逻辑,代码实现起来是非常困难而且容易出错的。
总之教训就是在边界条件,转移方程等等细节上面不要烦躁,不要讨厌,静下心来认认真真的推过一遍,觉得没有问题了再去砸键盘。
T2 神秘重题,也是线性基的板子题,没什么好说的。
T3 诈骗题,不过没骗到,也无话可说。
T4 正如题解的原话:很诡异的东西。最后的思路确实考场上不容易想出来,而且他描述出来确实也很抽象,不太好理解。
反正题解翻来覆去看了四五遍,视频也听了,还是没有搞懂他最后是怎么统计贡献的。
log.txt
0824:
Passed T1 all big samples EXP: 100pts
0842:
Passed T2 all big samples EXP: ?pts
(no ensurance about whether if it's correct)
0936:
Passed T3 all big samples EXP: 100pts
0940:
WTF is T4???
1107:
Passed T4 all big samples EXP: 60pts+10pts?
1226:
Feel like sleeping
25.8.19 比赛总结
神秘数据,得了 $300$ 分,其中 $160$ 分是数据水飞过去的?
对于 T1 来说,最大的问题就是不仔细读题,题目要求顺序完成任务,然后我选择排序后贪心,正常数据强度下差不多就没分了,然后出数据的人真给面子,送了 80pts。
还有就是对细节的思考不到位。题目中保证有解,于是成功被带偏,认为一定可以在一天内正常休息并完成任务。实际上可以休息很多天并蓄力一击。
对于 T2,大体上是做的没什么问题的。大方向是正确的,卡常也是差不多卡够了的,唯一的问题就是过于相信计算机的运行速度。理论上需要 3s 左右的算法没有想着继续优化,而是相信计算机跑的足够快。
最核心的 dp 方程没出错,但是不够优化,正解相当于是在我的方程的基础之上增加了费用提前计算,这时候就优化掉了在最终费用计算时较为重要的长度这一项。
也就是对 DP 中的一些简单但的不太常见的优化思路不熟悉。
T3 没什么好说的,考场上想到了关于正解的小部分要素,但是要凑出来正解还是没什么希望的,也就是跟着大部队骗完 30pts 直接走人。不过本来打的是 40pts 的,少打了一个取模!!!!!
T4 神秘数据,显然错误的贪心拿 100pts。想到了正解的大致方向,因为之前见过,但是具体的上下界不是很会处理,所以只能抛弃正解尝试去玩有点正确性的贪心,结果能过。无语。
log.txt:
0804:
Passed T1 all big samples with last TLE, but np.
0810:
Passed T1 all big samples. EXP 100pts
0851:
Passed T2 all big samples with last TLE(just for checking).
may try to optimize it later.
deprecated with 70pts
0939:
Deprecated T3 with 40pts
1003:
T4思路完全错误*1
1056:
T4思路完全错误*2
1112:
Passed T4 sample 1~4,exp:20pts
1122:
Passed T4 all big samples :)
in fact it's "lying" through the samples
EXP: 40pts?
1206:
Passed T2 all big samples. EXP: 100pts
1225:
Rejudged all programs on CBCOJ
EXP: 100+100+40+40-30=250pts
25.8.18 比赛总结
T1 是位运算类的板子题目,没啥问题。
T2,EMM,怎么做到的呢?第二轮思考了8分钟得出了正解(前三大值),然后果断放弃大方向明确的正解去打暴力,并且成功打挂分。
不过维护前三大值这个东西看起来真的很难做?你还需要知道这些值分别在各个子树出现了多少次,其实很难评价到底是不是一个正确的决策。yet is the best。
T3 一波神仙转化,但是见的多了仍没有引起足够的注意。
总结一下:一些树上统计问题可以利用dfs序或者欧拉序等,将点(不)在子树中的这一类限制转化为在序列的区间上,从而将路径在某些区间内转化为在某些矩形内,然后利用扫描线求二维面积并等问题。
这类题前面几乎每一场比赛都会有一道。难度确实也不小,容易出现在 T3/T4。
T4 神秘构造题,有点思路,一眼就是归并一类的东西,但是实在想不到什么有效的方法,果断优化30pts的暴力,然后拿了45pts。
log.txt
1423:
T1 Pass all samples exp 100 pts
1521:
# Deprecated T4 with about 30 pts
1552:
BF of T3
Deprecated T3 with about 45pts
1731:
BF of T2 with multiple bugs fixed
running on B3(not till end)
EXP: 50pts
1757:
# T4 Detailed points: 7+6+5+3*7=39pts
1821:
Updated T4
T4 Detailed points: 10+6+6+4+3*6=44pts
EXP:100+50+45+44=239pts
25.8.2 比赛总结
信竞队集体坠机。
第一题,别样的伪差分约束发力了,但却是还没太看明白题解,后面补一下。
第二题,神秘的图论性质发力了。考场上轻易的想到了生成树之后特殊处理经过了哪些非树边。
但是问题也就出在这里:哪些非树边而不是哪个非树边。我们不得不考虑经过哪些边,以及相关的顺序,
可是实际上数据范围是支持事先跑出若干个点的多源最短路的。也就是说我们可以预先找出一些点,让他们完全考虑所有的边。
我们也就不难想到事实上我们可以直接考虑枚举最近的非树边的点,并计算其答案,综合纯树边的答案求个最小值就行了。
也就是问题可能出在对另类最短路的常见性质了解不足。另外考场上也受之前的经验限制,一直在想怎么处理强连通块内的距离,仿圆方树的方式进行处理。
第三题,神秘的调和级数又发力了。一种正解:枚举 $d$,考虑倍数 $k\times d$,最大值为 $d$ 的答案就是 $\frac{n}{d^2}\times\frac{m}{d^2} - \sum \frac{n}{(kd)^2}\times\frac{m}{(kd)^2}$。大到小枚举即可。
对比考试时的思路,发现容易地想到了枚举 $d$,但是在使劲的考虑怎么使用 $\mu$ 一类的东西进行容斥限制 $\max$ 的条件。同时也发现了平时常用的容斥技巧失效的原因是 $kd^2$ 中的 $k$ 不一定是平方数,但随后证明了 $k$ 是平方数的时候才有效。
不得不说,问题大概率出在这里,尤其是遇到和倍数相关的容斥的时候首先就应该考虑直接枚举倍数,多数情况下会是调和级数的。其次就是和前文记录 $64$ 类似的毛病:容斥的只需要管好本身的贡献,多的少的让容斥自然解决,而不是尝试自己消化掉。顺着错误思路下去,连基本的贡献都被否决了。
第四题,神秘玩意,看看题解突然感觉这套题是不是按难度倒序排序的?最基本的结论也没推出来几个。从大往小推这点就没推出来,就完全做不了了。
总之就是这样那样的一堆问题,当场坠机。不过难度倒序排序的诗人啊!
25.07.12 比赛总结
暑期集训的第一场比赛,算是开了个好头。话说这个博客中的内容时间跨度已经整整一年了呢。
T1 没什么好说的,普及组 T2 难度的,符合 CSP2024 实际情况。
T2 就很有意思了,这是一个有大大的后效性的 DP,考场上直接愣住了,没想出来有效地处理方式,最后遗憾的 $O(n^3)$ 骗部分分走人。
事实上这个 DP 很具有启发性。这个 DP 我们发现他没有前效性:只要你前面选了,不管你后面怎么走他的贡献都是不会变的,因此我们可以直接考虑将整个 DP 的过程倒转一下,这样子就从没有前效性变成了没有后效性,可以直接省掉一维时间做到 $O(n^2)$。
事实上你也可以认为它使用了类似于代表元的思想,也就是说我们不管绝对位置,只要相对是那样的,反正对结果没有影响,那我们就不去具体处理。
好题,出题人厉害!
T3 的题解似乎用了不那么规范或者说常见的表述:“偏序”。这里可以理解为排序后第一个序列在对应位置小于等于第二个。
用到了一个结论:一个长度为 $2n$ 的括号串合法,当且仅当所有左括号的位置能被$1,3,5,7,\dots,2n−1$ 偏序。
于是我们就可以对于每一个数记录出他的相同类型的数的出现位置,能匹配就匹配,只能匹配一半就是匹配不上。匹配不完也是匹配不上。
那就做完了。这个别样的结论之前没见过,说实话其实也算不上巧或者妙,只能说多积累一个形式。
T4,考场上直接转化成图论问题,是一个 $O(n^2)$ 的相对简单的算法,随后发现有简单好写,到处乱创的 $O(\frac{n^3}{w})$ 做法,毅然放弃 $O(n^2)$,别样的。
当时放弃主要是因为即使转化出了最后的图,时间复杂度也还是太大了,不能通过。那三种要减去的情况算出来了也没用。
谁知道出题人硬是用扫描线和线段树、树状数组什么的硬是飞过去了,数据结构仙人,佩服,但是具体维护一点都不讲是什么鬼啊!
东骗一点,西骗一点,硬是骗到了差两分上 $300$,属实炸裂。
25.06.21 比赛总结
T1 倒是做的比较干净利落,$20$ 分钟切掉了,主要问题出在后三道题。还原一下 log:
20min: 过第一题
20~25min:浏览二三四题,“发现”第四题子集反演
25~85min:磕T4
85~110min:打 T2,T3 暴力
110~130min:磕T4,发现基础结论和算法全错
130~145min:打 T4 暴力
145~170min:磕 T3,转化为最小环
170~180min:闲着(原本应该170min就交了)
170~180min:随便给 T1 输了几个小样例,全是 hack(汗)
(180min)交代码
185(+-3)min:发现 T3 交错代码爆零了(啊!!!!!!!!!)
T2 之前做过,考场上认出来了原题,但是方向错了。这道题显然可以用点分树做。但是时间紧,加上自己之前完全没写过,不敢在考场上手搓,就毅然决然的在 $20$min 的时候放弃了。
事实上,这道题也牵出了一个我已经忘掉的结论:对于一棵树 $a$,他的直径是 $(l_a,r_a)$ 的话,那么加入 $b$ 之后的直径只会是 $(l_a,r_a),(l_a,b),(r_a,b)$ 之一。说句实话 ,这个结论还是太难用到了,但是终究是见过的,不该忘了。
T3 多给点时间应该可以做出来。在第一次看的时候就在 $10$s 之内发现了最多 $2$ 个质因数的性质。第三段磕这道题的也顺理成章地转化到了最小环。
问题就在于怎么想到必定经过 $1000$ 以下的点,以及用 BFS 快速统计环长。事实上第二点的正确性是基于第一点的,但是个人认为多给一点时间一定是想得到的。
T4 的话应该一方面是思维惯性,卡在子集反演出不来了,第二方面是对小数据范围的常用技巧型整理不是很恰当。
重点真的在第二点。很早之前就提出过要整理 tricks,但实际上并没有一个很系统的整理,很大程度上在靠考试时的思维随机游走。
必须整理起来了,还有大概 $4$ 个月的时间,也够整理不少的。
还有第三点就是决策失误了,刚开考一小段时间就去死磕 T4 一般来说并不是一个明智的选择。
还是那个老大难问题:每一个问题或多或少都能想到最核心的那么一些部分,难题目前来说想磕出来还是靠“拼凑的断章”。step-back 已经逐渐失效了,需要找一些更有效的方法。
25.06.07 比赛总结
第一题敲出了正解,但是有更为简单的解法,分析错了时间复杂度,而且不假思索地放弃了,该罚!(雾)
第四题竟然考了不知道什么时候学过一遍的虚树,虽然说线段树合并,DSU on tree 什么的也可以卡过去。
不过这一次有一些比较神奇的事情:每一道题都或多或少的想到了正解中比较核心的一些部分。
第二题可以算是半个 AD-hoc,考场上已经发现了每一个数对应一个唯一的 01 序列。并且通过 trie 树将问题转化为了树上的问题,唯一的问题在于没有发现当 $m>2\times\log_2n$ 的时候因为最优策略答案必然为 $0$。
这确实好像有点隐蔽,不是很好 说什么,或许要增强一下对于特殊性质的发现能力吧。
第三题其实已经想到了通过向因数连边来间接建图,优化复杂度,毕竟之前见过,也没有什么好说的,也会用 tarjan 求出来割掉后的最大的连通块的最小大小,毕竟这是练习题里面有的。
但是也存在两个的问题。一个就是我们常提的简化状态的思维。对于这道题,只要是两个及以上的可重的质数相乘,结果就是合数。而恰好两个乘起来的就是其中最简化的状态。当发现 $10^7$ 以下合数过多的时候并没有往这方面去想。
第二点就是懒。如果我抛开合数过多硬去写代码的话仍然可以获得 $52+pts$。但是我却认为这样子代码过长,性价比不高,转而去磕 T2,T4 了。思路没有问题,但是有思路不写转而去整其他的似乎并不是一个明智的选择。
第四道题想到的确实就比较少了,但是固定一条路径去找另一个路径的核心思路确实想出来了,这样子如果打一个线段树合并什么的其实已经能过掉 $10^3$ 级别的点了。
别的不说,这道题的题解和 STD 也是一坨,$f(u,v)$ 只和 $\operatorname{lca}(u,v)$ 相关,然后硬是被写成了 $A_u+A_v+B_{\operatorname{lca}(u,v)}$,对着 STD 理解发现一点注释没有。
好歹给个正经点的式子啊!这改不了一点。
25.05.04(ARC197)比赛总结
显然是高估了赛题难度的,过早放弃,实际上还能做出来。
尤其总结一下 T2,T3,T5。
T2 思考了半个小时后放弃,但是实际上此前已经想出了一个非常接近正解的突破口。重新打的时候顺着这个口子又想了一小会儿就想出来了。
T3 思考并实践了一小会儿也放弃了,这道题主要是几个性质+结论:
- 调和级数 $O(n\log n)$;
- 如果一个数被删,就不可能去删掉别的更多的数;
- 一个质数只能被自己删掉。
以后再遇到倍数相关的问题的时候,可以重点看一下最后两条性质。显然我在考场上并没有想到这些,尤其是第三点,让我以为答案会在 $10^{18}$ 量级从而放弃思考。
T5 其实有一点,最开想的时候想复杂了。正难则反,考虑倒着计算会更靠谱一些,但是我便要正着想,推了半天式子发现情况过多,放弃思考。
就是说有的时候其实换一个思路去想会更好一些。
25.04.19/24.10.19 比赛总结
文件包。
为啥放一起了呢?上一次没总结,这一次考了上一次的题。
对比一下两次的成绩,不难发现,有明显变化的题就只有 T2,不应如此。
T1 就是防爆零的题,或者说难度很低,两场都做起了,没什么好说的。
T2 这一次成功的做了出来。究其原因有两点:其一是最近正好做了大量的数据结构题,对此类问题较为敏感,第二是因为考场策略优化,stepback 终于落到了笔头上,更加高效的重发现了有用的性质。
T3 本应可以做出来。此前已经多次遇到除以一个数下取整后整个区间修改的类型的题,也明确知道这个是 $log$ 级别的,但是考场上似乎再一次忽略了这一点,造成了较为严重的丢分。
T4 也有一些问题。考场上能想到一个大致的思路,剩下 100 多分钟却仍然选择苟着骗分。这种状态下明显可以选择试一下的。需要改进。
总的来说就是两大点:第一,保持落在笔头上的 stepback,如果没有条件一定保留除草稿外的所有信息;第二:Just do it!有条件研究一下的题一定要去好好的写一下,不要贪省事。
25.3.15 比赛总结
文件包。
T1 不说了,就是防爆零的。
T2 再次为我们敲响了警钟:能不用哈希的时候一定不要用哈希,一定要用的话考虑双哈希起步。到目前为止这道题没有人用哈希而且没被随机数据卡。
T3 思路真的是太巧妙了。另提一句:发现了一个神奇的性质之后不要觉得没用就抛弃了。你永远也不知道一个神奇的性质是不是这个题的突破口。
25.3.1 比赛总结
不得不说 T1 有相当明显的复习意义。当我推出来 $a_i=2\times b_{i-1}+1,b_i=2\times b_{i-1}+a_{i-1}+2$ 的时候,我并没有想到使用矩阵快速幂去优化,而是尝试着去推通项。
但是这也确实帮我避了雷,我利用 $a_{i-l},b_{i-l}$ 到 $a_i,b_i$ 的转移去推 $a_{i-2\times l},b_{i-2\times l}$ 到 $a_i,b_i$ 的转移,常数略小于矩阵快速幂,从而仅仅使用快速幂就卡过了这道题。
事实上这道题提到的光速幂也和 BSGS 的思路有几分相像,可以记一下。
T2 就非常悲催了。我已经推出了他会形成一个或多个环,环间独立,然后固定最大的去玩后面的的正确方式,却没有想到将二者结合一下。
结合一下就能得到一个比题解的解法更简洁也更好写的做法。至于 T3,T4,骗骗分可能没太大的问题,但是写正解,尤其是 T3 的话还是太吓人了。
$\texttt{stepback}$ 是个好东西,下次必须写上!不然自己想到过什么都不知道。
25.2.26 比赛总结
这坨总结包括 $02.08,02.10,02.12,02.14,02.18,02.20,02.25$ 的总结,且只总结部分有价值的题目。题目包。
$02.14$ 及以前那些是寒假打的,基本上就是按照以前总结的哪些方法在做,没出什么事,也就没有什么好说的。
$02.18$ 启示我们注意枚举顺序。有时候人为限制一下大小关系,枚举顺序就很关键了。比如 T1;有时候大段的枚举是等价的,考虑快速找到等价段的左右区间,比如 T2,除法分块亦同。
$02.20$ 的 T2 是一道好题,思路非常清奇,详见题解。像这种小清新题,一定要先观察性质,比如两个问题在一定的情况下是不相关的;然后观察数据范围,找合适的数据结构维护他。不可多见的清新题。
$02.25$ 在 T1 出了一个错误,必须指出,防止再犯:在类字符串哈希的时候,一定要 $h_i=h_{i-1}\times p+v_i$,而不是 $h_i=(h_{i-1}+v_i)\times p$。这样做的话无法正常判断 $v_i$ 顺序不一的情况。鬼知道为什么会犯这种神奇的错。
总的来,有一些想要提醒一下:
-
当遇到一道题中出现了某个值范围较小时一定要注意思考一下,可能就是突破口。比如:0208T4。
-
如果一道题,你只能整出相对优一点的解法,那一定不要吝啬你的空间,在空间能接受的情况下尽可能开打数组,万一数据水直接过了呢?比如:0210T2。
以及一个 tricks:当你动态规划时涉及选择,并且对最大最小值有特殊计算方式,那么你可以将选择集合排序,然后标记是否选择最小最大值。比如:0208T2,0210T1。
24.11.23 赛后总结
题目
文件包。
问题分析
T1
首先,不要在 T1 上花太多时间纠结到底写什么;其次,不要在 T1 上花太多时间纠结到底写什么;最后,不要在 T1 上花太多时间纠结到底写什么。(重要的事情说三遍)。
就是说,算法已经优到打表只用 $10s$ 就能打完你还写什么正解?不如直接分段打表走人。
T2
题目背景挺有意思的。这题确实略比 T3 难。
考场上已经想到了 $O(nm^2)$ 的算法,但是没有想到用记录这一个点前的区间数量来优化到 $O(n^2m)$。
很有意思的一道题,也给我们一个提示:对于 $n\times m\le v$ 类型的数据范围,可以考虑一下能不能保证或者特判掉 $n>m$ 的情况,这样子 $O(n^2m)$ 实际上就是 $O(v\sqrt v)$。
毕竟也不是第一次遇到了。上一次好像没太在意。
T3
std 用的是 $O(\sqrt n)-O(1)$ 的神奇分块。但是我并没有想到这一点,我想到了暑假学的一个神奇技巧。
对于 $x\le lim$ 的情况,统计其出现次数,计算答案时合并贡献;对于 $x>lim$ 的情况,暴力统计他对值域内的 $y$ 的贡献。
不难发现,第一类操作的复杂度为 $O(1)-O(lim)$,第二类操作可以使用树状数组优化,复杂度为 $O(\lfloor\frac{v}{lim}\rfloor\log lim)-O(\log lim)$,其中 $v$ 为 $y$ 的值域,即 $4\times10^5$。
总的复杂度可以视为 $O(\lfloor\frac{v}{lim}\rfloor\log lim)-O(lim)$。理论上 $lim$ 在 $1800$ 左右时上式子值较小,但是因为数据随机,所以在 $lim$ 取 $1000$ 左右时更优。
T4
又是一个贡献转期望的神奇问题,之前也遇到过,觉得能转的就只有几道题,没太在意,就寄了。
不过,这道题我连转化需要的贪心解都没有给出来。在那之后用一下树上的 DP 就差不多结束了。
总体感想
还好,考场上想拿的分基本上都拿了。T2 挂了不少分,虽然没找出来原因,但是毕竟是匆忙中赶出来的代码,也就不去深究了。
整体的话没出什么大问题,就是喝水喝的有点勤?
24.10.13/15 赛后总结
题目
问题分析
T1
没什么,跑的飞快,过了。
T2
没什么,考场上及时放弃,策略正确,拿了点暴力分。
T3
没什么,考场上成功被大样例坑掉 $45pts$,不是很有话说,除此之外,该拿的都拿了。
T4
显然,考场上的式子推的有些复杂,能支持到比原题更全的信息,有冗余信息的记录,下次注意一下能不能简化。
T1
没什么,这个 checker 怪怪的。
样例有那么一点点弱,也有一点点少。
现在没事了,这数据有一一四五一四点强。
T2
没什么,考场上整出了 $len\le5$ 的,就根本没想到双向搜索。所以按理说这道题卡卡常能支持到 $10$?总之这不重要。
T3
考场上玩式子的时候整错了一些部分,以及不合理的状态设计,导致代码细节巨多,不想调放弃了。
以后要注意一点:对于树上的静态信息的维护,如果可加减就优先考虑一下树上前缀和,不可加减的话就考虑一下树上倍增。总之,不要写像 std 一样的树剖,常数又大,还难调。
T4
一道怪怪的题,要数学不数学的,最后整出来了一个 DP,考场上连最起码的 $1,2,5,10$ 的分都没拿到,那我也是没什么好叫的了。
总体感想
没话说,这两天总共写出了两个隐性的正确性换时间的剪枝,一次忘记开暴力开关综合上四个过水的样例,覆盖四道题,共计多挂了 $120+pts$,原地高血压。
以后还是多造几组小样例吧,可能有点用。
主要是改错的时候,这些错误全部是在大量的对拍后才发现的,就很烦了,考场上找出来就有点难了。
24.10.05 赛后总结+集训总结
题目
问题分析
T1
没什么好说的,几分钟切了。比较水。就是两道题缝了起来。
$\textit{step-back:Empty}$
T2
思路异于 STD,讲一下:
我们考虑两个点之间的最大路径中的最小值,如果我们将点按点权从大到小加入其中,那么两点第一次连通时这个点就是二者之间的最大值。
那么思路就很显然了:统计大小的并查集。假设点 $p$ 连通了 $k$ 个原有的集合,其大小分别为 $s_1,s_2,\dots,s_k$,那么贡献为 $(\prod_{i=1}^k \prod_{j=i+1}^k s_i\times s_j+\Sigma_{i=1}^k s_i)\times v_p$。显然,二者均可以通过统计和与平方和线性求出。最后合并一下就完了。
$\textit{step-back:}$
/*
step-back:
首先最暴力的就是建图考虑优化。
我们注意到,我们要求的就是二者之间的最大的路径。
一个很神奇的思路呼之欲出:从大到小加点。
点到为止,已经很简单了。
*/
代码如下:
#include <bits/stdc++.h>
using namespace std;
constexpr bool online = 1;
#define int long long
struct node {
int p, v;
inline bool operator<(const node& r) {
return v > r.v;
}
}v[100005];
vector<int>son[100005]; int n, m;
int f[100005], sz[100005], ans; set<int>s;
inline int find(int p) {
return f[p] == p ? p : f[p] = find(f[p]);
}
inline int siz(int p) { return sz[find(p)]; }
inline void merge(int l, int r) {
l = find(l), r = find(r);
if (sz[l] < sz[r]) swap(l, r);
f[r] = l; sz[l] += sz[r];
}
inline int sqr(int x) { return x * x; }
signed main() {
if (online)
freopen("run.in", "r", stdin),
freopen("run.out", "w", stdout);
ios::sync_with_stdio(0);
cin >> n >> m;
/*
step-back:
首先最暴力的就是建图考虑优化。
我们注意到,我们要求的就是二者之间的最大的路径。
一个很神奇的思路呼之欲出:从大到小加点。
点到为止,已经很简单了。
*/
for (int i = 1; i <= n; ++i)
cin >> v[i].v, v[i].p = i;
for (int i = 1, a, b; i <= m; ++i)
cin >> a >> b,
son[a].emplace_back(b),
son[b].emplace_back(a);
sort(v + 1, v + n + 1);
for (int i = 1, ps; i <= n; ++i) {
ps = v[i].p, f[ps] = ps, sz[ps] = 1;
int spf, pfs; spf = pfs = 0; s.clear();
for (int sp : son[ps])
if (f[sp]) s.insert(find(sp));
for (int sp : s)
spf += sz[sp], pfs += sqr(sz[sp]),
merge(ps, sp);
ans += (sqr(spf) - pfs + spf * 2) * v[i].v;
}
cout << ans << endl;
return 0;
}
T3
以后玩这种空间大的题一定开任务管理器看!没计算递推栈空间开销,然后 MLE 了。
$\textit{step-back:}$
/*
step-back:
我们注意到这个值总是在变小的,变为零之后就不动了。
我们能想到什么?树上 k 级祖先。
点到为止,不做赘述。
难点好像在于压缩空间。空间不够。
最多只能跳 14570 次
*/
T4
判断失误。自己手写的分块,误认为在某种特殊构造下会很慢,然而通过了极限数据,但实际上随机数据会把它卡到飞起。
实际上我的暴力本地跑的时候完全过不了 $70pts$ 的有针对性的极限数据,但显然邓老并没有针对性。多挂 $20pts$。
$\textit{step-back:}$
/*
step-back:
保留一份暴力:
n = read(); m = read();
for (int i = 1; i <= n; ++i) a[i] = read();
for (int i = 1; i <= m; ++i)
if (o = read(), l = read(), r = read(), o == 1)a[l] = r;
else {
memcpy(v + 1, a + l, (r - l + 1) << 3);
int ln = r - l + 1; sort(v + 1, v + ln + 1); ans = 0;
for (int a = ln - 2, b = ln - 1, c = ln; a > 0; a--, b--, c--)
if (v[a] + v[b] > v[c]) { ans = v[a] + v[b] + v[c]; break; }
writi(ans);
}
我们来思考一下一个最长的没有三角形的序列长什么样:
1 1 2 3 5 8 13 21 34 55 89 ...
这不是斐波那契数列吗?
那么在 1e8 范围内他有多少个值呢?39 个。
这说明,在我们求解的范围内:
若超过39个,则在前39个内一定有解;
不足39个,可以暴力。
考虑一下能不能分块。
块数不是很好定。修改复杂度为 l*log(l)。
但是注意到,我们可以延后重构操作:仅当查询到时才重构。
这样子每次修改的复杂度均摊就不大于 l*log(l) 了。
想一下查询的细节。我们需要扫描每一个块,该重构就重构。
然后保险一点,取出前 40 个,时复应为 40*(n/l), 不能太大。
这个限制 n/l 在 50 左右,也就是块数在 50 左右。
这样一个块最长就是 2000,要炸。
赌一下,机子跑的快一点,每个块只给 500。
修改常数小得多,心理博弈开始。
*/
总体感想+集训总感想
本场比赛炸出了一个以前从未遇到的问题:计算空间时未考虑栈空间开销从而炸空间。吃一堑长一智,别二犯就好。
这几天有悲有喜。既有被金宝碾掉的时候,也有霸榜整层楼的时候。从总体来看发挥良好,很在状态。
这几天主要犯的错就是空间计算错误,意外的越界和一些考场常见情况导致的判断错误与决策错误。
最重要的经验就是:死磕简单的题,容易拿的分一定要拿到手,后面难题的尽可能多想部分分,省一就有了。
总版(弃用整理至此)
24.10.04 赛后总结
题目
问题分析
T1
越界了,死得很惨。
下次遇到这种题最好自己写一个 calc 函数,直接判有没有越界,或者用 STL,防止这些奇怪的事故再发。
话说为什么就一个点卡我啊啊啊啊啊啊啊啊啊!!!
T2
就是一个简单的贪心,没什么好说的。
T3
决策性错误:误认为 T4 很难写而死磕,然后啥也没磕出来。赛后发现代码部分与 STD 很像,但是没理解到 STD 的意思。
T4
决策性错误:误认为 T3 可以磕而放弃,然后只写了个暴力。赛后发现思路与 STD 很像,然后因为 memset(this,0,sizeof this) 调了一下午。
请一定注意:sizeof(this)!=sizeof(struct)。this 的大小会比 struct 多出虚函数的表等一堆其他的东西。总之,能直接赋值就不要 memset 这一整个结构体。
总体感想
没什么感想。书言已尽,前天的总结已经够用了。
24.10.03 赛后总结
题目
问题分析
T1
DP,终于是磕出来了,但是思路不太一样。简述一下:
同时处理两个 DP 数组,分别维护形如 (...+...*...+...*...)+... 的式子和形如 (...+...*...+...*...)+...*... 的式子。对应代码中的 dad 和 dti 数组。每个数组均维护三个值 $a,b,c$。
状态设计:
对于 dad,对应关系如下:
/*
(...+...*...+...*...)+...
--------------------- ---
a b
以及 c 表示在这个点的这类算式的个数。至于为什么会用到后面会说。
*/
对于 dti,对应关系如下:
(...+...*...+...*...)+...*...
--------------------- ---
a b
-------
c
设计的很奇葩,但是后面会讲怎么转移。
特别注明,这里所写的 $a,b,c$ 均指同一位置上同一形式的算式的 $\Sigma$ 值。
接下来讲转移。
如果这个点是 *,那么 (...+...*...+...*...)+... 转为 (...+...*...+...*...)+...*...,将 dad.a 转存入 dti.a,将 dad.b 转存入 dti.b,抛弃 dad.c,将 dti 中的值压缩存入 dti 中。具体的,将 dti.a 放入 dti.a,随后将 dti.c 存入 dti.b,抛弃 dti.b。(这里的第一个值指前一状态的)。
相应的,你可以自己手玩一下另外两个情况。
边界状态:dad[1][1]={0,c[1][1],1}。
答案:dad[n][m].a + dad[n][m].b + dti[n][m].a + dti[n][m].c。
下面是核心代码。还是建议先自己手推一下,再来看代码检验。
//核心部分
node au = dad[i - 1][j],
tu = dti[i - 1][j],
al = dad[i][j - 1],
tl = dti[i][j - 1];
/*
重新设计 node 状态表示:
dad:
a:前面的加数之和;
b:最后一个加数的当前值;
c:加法算式个数;
dti:
a:前面的加数之和;
b:第一个乘数的值之和;
c:乘积之和的值。
特别注意:
对于 dti:(a,b,c) 遇到一个数 k:
变为 (a,b,c*10+bk)。推导:
有 a1+b1*c1,a2+b2*c2,...
遇到 k:
a1+b1*(c1*10+k)+a2+b2*(c2*10+k)+...
= (a1+a2+...)+10*(b1*c1+b2*c2+...)+k*(b1+b2+...)
*/
if (c[i][j] == '+') {
mad(dad[i][j].a, moad(au.a, au.b));
mad(dad[i][j].a, moad(al.a, al.b));
mad(dad[i][j].a, moad(tu.a, tu.c));
mad(dad[i][j].a, moad(tl.a, tl.c));
//a 处理完毕,b 直接默认 0
dad[i][j].c = cvl(i + j - 2, j - 1);
//c 处理完毕
}
else if (c[i][j] == '*') {
/*
加法:a1+b1*,
即变为 (a1,b1,0)
乘法:a1+c1,和b1
即变为 (a1,c1,0)
//attent: ((sig),(sig),0)
*/
mad(dti[i][j].a, moad(au.a, al.a));
mad(dti[i][j].a, moad(tu.a, tl.a));
//a 处理完毕
mad(dti[i][j].b, moad(au.b, al.b));
mad(dti[i][j].b, moad(tu.c, tl.c));
//b 处理完毕,c 直接默认 0
}
else {
/*
加法:
a+b -> a+(b*10+k)
a 不变,b *= 10,b += k*c;
乘法见上:特别注意:
对于 dti:(a,b,c) 遇到一个数 k:
变为 (a,b,c*10+bk)。
*/
mad(dad[i][j].a, moad(au.a, al.a));
mad(dad[i][j].b, (au.b * 10 + (c[i][j] ^ 48) * au.c) % mod);
mad(dad[i][j].b, (al.b * 10 + (c[i][j] ^ 48) * al.c) % mod);
mad(dad[i][j].c, moad(au.c, al.c));
mad(dti[i][j].a, moad(tu.a, tl.a));
mad(dti[i][j].b, moad(tu.b, tl.b));
mad(dti[i][j].c, (tu.c * 10 + tu.b * (c[i][j] ^ 48)) % mod);
mad(dti[i][j].c, (tl.c * 10 + tl.b * (c[i][j] ^ 48)) % mod);
}
T2
很好,也磕出来了。但是还是和正解不一样。
接下来说“正解”:我们枚举同一行上的点,比如我们枚举了 $(x_1,y)$,这时候,我们找出所有在同一列上的点 $(x,y_1)$,计算此前出现过多少次 $y_1$ 并记入答案贡献,此后将 $y_1$ 在桶中加一。
很显然,这个算法在面对网格式的数据的时候时复会被卡满,也就是形如这样的:
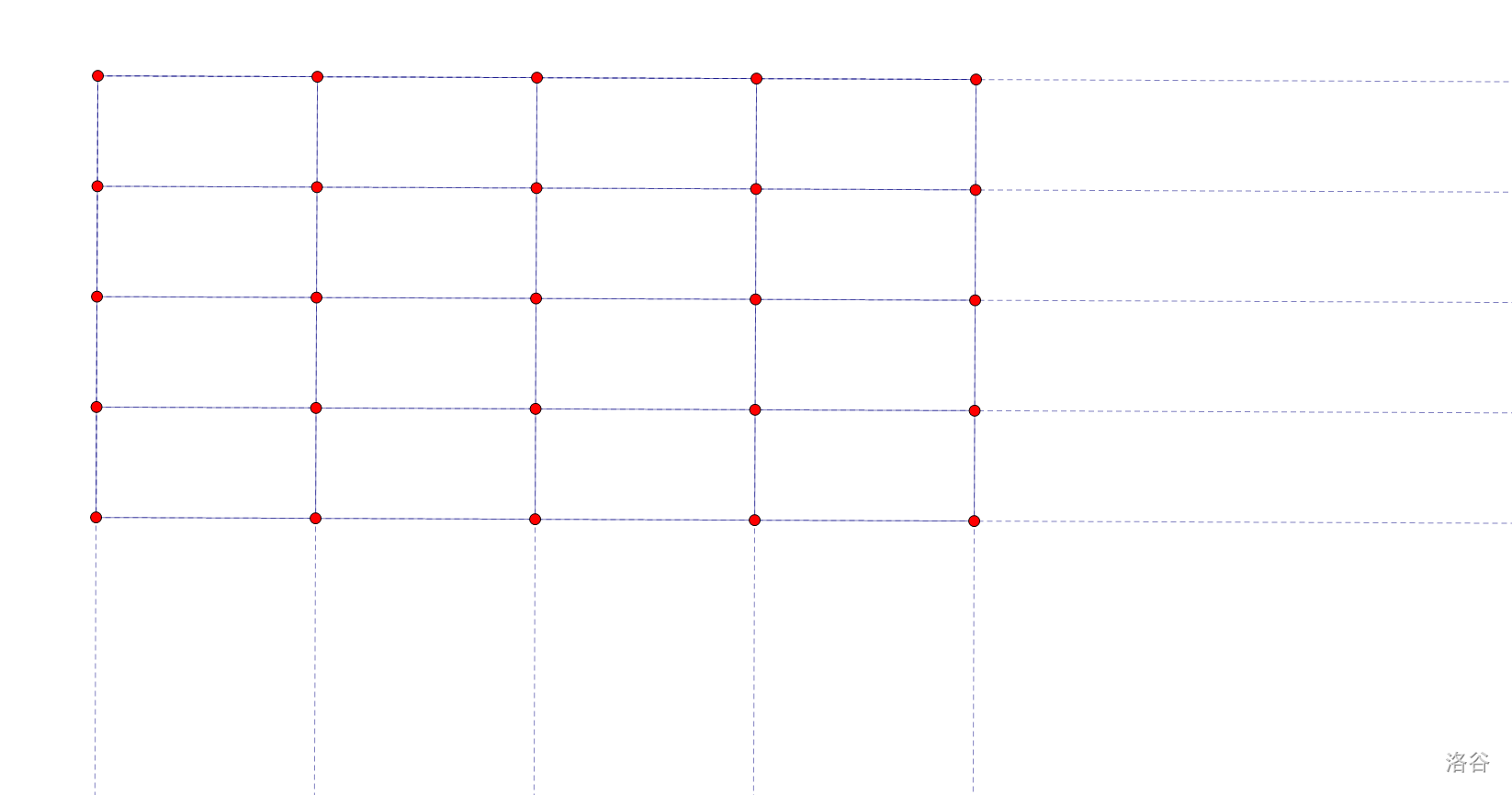
接下来就是分析复杂度了。我们假定 $xy=n$。($x,y$ 为横纵数量)。
显然,每一行都是 $n$ 的复杂度,我们可以通过转置的方式使其宽度保持在较低值,为 $\frac{n}{4}$。总的复杂度为 $O(n^2)$。但是常数贼小,卡卡常就能过极限数据。
给出一份过不了的:
for (int i = 1; i <= n; ++i)
cin >> x[i] >> y[i], sx.emplace(x[i]), sy.emplace(y[i]);
if (sx.size() > sy.size())
for (int i = 1; i <= n; ++i)
swap(x[i], y[i]);
for (int i = 1; i <= n; ++i)
pos[x[i]].emplace_back(y[i]),
poy[y[i]].emplace_back(x[i]),
s.emplace(x[i]);
for (int xp : s) {
for (int np : pos[xp])
for (int yp : poy[np])
if (yp != xp)
if (t[yp]) ans += t[yp], t[yp]++;
else t[yp] = 1, cv[++cn] = yp;
for (int i = 1; i <= cn; ++i)
t[cv[i]] = 0; cn = 0;
}
cout << (ans >> 1) << endl;
T3&T4
这两题没什么好说的,该拿的暴力分都拿了。
总体感想
昨天总结的挺好,今天实践有效,不再做总结了,直接沿用昨天的经验。
俩机房的 RK1,大吉。
24.10.02 赛后总结
题目
问题分析
T1
好好的记住这个式子:$\Sigma_{i=1}^{n}\frac{1}{i}=O(\ln n)$。调和级数。考场上受到之前一道分块题的影响误认为这个式子是 $O(\sqrt n)$ 的,于是寄了。
另一点,除非在十分肯定代码能稳过极限数据,否则一定要把所有能加的各种优化都给加上。加上分数只升不降!
T2
确实就是能力有点有限了。很轻易地就能想到按位分,但是这个方向实现还是有一定的难点。
正解相对会简单一些。首先,我确实想到过当我们将运算符按照 &&&...&&|||...|| 的形式排列能取到最大值,但是倒序的字典序阻止了我继续想下去,没有想到换位置来优化他。
T3
这题没什么好说的,死了就是死了,大分讨谁爱写谁写。考场上的连链状的都没调出来,正解就算了。
还是出了正解思路的:讨论横插返祖边就行。
T4
确实恶心,这种东西能靠推式子简化,考场上知道基本也推不出来。
总体感想
冷静沉着,深度思考。勇敢的放弃,把时间放到简单题上,难题骗分暴力自选。
前两道题还是该死磕一下的。
比赛总结合集(24年暑假)
-
暑假前期的比赛和集训就此告一段落。比赛总结全部收录至此。
-
全部试题,本人赛时程序,改错程序和 std 将会稍后在此处更新。
Test Blog List
| 博客链接(弃用整理至此) | 题目-题解 | 程序包 | 分数-排名 |
|---|---|---|---|
| 24.7.8 | 题目-题解 | Nan | Nan-Nan |
| 24.7.9 | 题目-题解 | cpp | 124-4/8 |
| 24.7.10 | 题目-题解 | cpp | 205-3/8 |
| 24.7.11 | 题目-题解 | cpp | 195-5/8 |
| 24.7.12 | 题目-题解 | cpp | 150-6/8 |
| 24.7.13 | 题目-题解 | cpp | 185-6/8 |
| 24.7.15 | 题目-题解 | cpp | 20-8/9 |
| 24.7.16 | 题目-题解 | cpp | 70-6/9 |
| 24.7.18 | 题目-题解 | cpp | 120-7/9 |
| 24.7.19 | 1234-1234 | Nan | 170-8/9 |
| 24.7.20 | 123456-123456 | Nan | 3(ICPC)-1/9 |
好吧,虽然这样拉通来一看感觉我就是个废物,但还是放到这里吧。
7.8,电脑无法访问(物理),改错记录:
// 7.9:124->220
// 7.10:205->305
// 7.11:195->400
// 7.12:150->310
// 7.13:185->395
// 7.15:20->300
// 7.16:70->300
// 7.18:120->310
// 7.19:170->400
// 7.20:3->4
24.7.20 赛后总结
题目
题目列表。
这次比赛略微的不一样了一些。$2h$,$6$ 道题,其中前三道为普及难度,后三道为提高至省选难度。
这次就真的没什么好总结的了,考场上能拿的分都拿完了,拿不了的基本上也没啥希望。
24.7.19 赛后总结
题目和题解均在洛谷上。列表。
问题分析
T1
发现了 luogu 和 lemonlime 的问题:对空间的计算不正确。本地开任务管理器测出 $507.9MB$,洛谷上 $512MB,MLE$,lemon 上空间限制 $512MB$ 就 $MLE$,限制 $1024MB$ 就 $511.68MB$ 。
当然,也有自己的问题。这一题考场上花了整整半个小时,原因是在那里写 trie 树。原因是当时分析需求,发现需要能够快速的求出有没有字典序比某个特定的串更小的串存在。
从这一点上讲去写 trie 是没有太大的问题的,但是因为贪心后,这些串被排了序,因而每一个串都是单增或单减的。其中存在的串全部单减,查询的串全部单增。因此只需要比较第一个字符就可以了。
这题本身其实肯定可以再加强一下数据,把 $n$ 再扩大一点,但是能想到上面的就一定已经能够做出来了,没必要再加强了。
所以说一份代码莫名 Hack 掉了两个知名的 Judger 是吧?
$100pts$,等于预期。
T2
好像之前在学习基环树的时候有看到这道题,但是当时没去做。记住了,下次还敢(雾)。
$40pts$,小于预期 $50pts$。
首先分析分少在了那里。经过和代码注释的对比得到:少了 Task7 的 $10pts$。再结合提供的题面和样例范围得出结论:缺乏对应的样例,导致考场上并未正确的检验其正确性。
所以说,考场上还是要自己造几组略微复杂的样例看一看。
再综合分析思路的问题。
其实,最接近正解的部分就是因为没能调出来而被禁用掉的第三部分暴力,其中主要内容是我之前所出过的题:并裂查集。这当中就包含了两种正解思路:并查集和拆点。事实上,若再仔细看一眼我的思路倾向的话,可能会相对的更加接近第二种一些。
论考场上的话,我甚至在这部分考虑过拆点再建图,然而并没能更深入地去思考,从而错过了正解。
给出一个解决方案吧。其实这在前天陈彦兴学长的分享交流中有提到,我很早以前也有想过,但是最后被弃用了,就是把你想到的东西写下来,当你发现想不动了的时候可以往前倒退几步而不是从头开始。
个人认为这可能会对我这种天天擦正解的边又天天写不出正解的人作用比较大。
T3
$30pts$,小于最低预期 $35pts$,暴力当中有一个点 WA 了,并没能找出原因,数据太大了。
题解的第一篇确实讲的特别好,其中有一个名称我特别赞同:特殊性质题。“就是题目给出了你极其神秘的性质,从而引导你想出正解”。
我考场代码就只走到了题解中的第一步:暴力,然后看着那个特殊性质就特别的蒙,什么也不知道,然后放弃了思考。
所以说,还是引用一下陈彦兴学长的观点:省选比 NOI 简单在省选会告诉你一些性质,问你怎么利用,而 NOI 需要自己发现性质,然后自己想怎么利用。像这种省选的题,告诉了你性质,那就看一眼。傻看也是不行的,你要看一看这个性质对你的程序而言有没有什么特殊的限制条件产生,进而思考这个限制条件怎样利用到更大的范围或者全局范围。
即便如此,这个思路也是非常巧妙的。因为我并没有意识到这个最小值对前后位置选择的限制作用,自然也就利用不来。这个东西,其实应该是结合着暴力代码的 $dp$ 数组的数值才能看出来的。
$\color{red}“最难的就是‘不难发现’。”$
T4
$0pts$,小于预期 $8pts$。说白了就是最暴力的暴力打挂了。
这个题虽然不是特殊性质题,但是跟着分值设定一步一步的打部分分就能够打出正解。
所以说,像这种题,在没有足够的水平之前可能还是比较耗时间的,毕竟你每走一步都得去想怎样优化这个东西。
考场上其实还犯了一个错误,当时还剩下半个小时多,足够我把区间 DP 给调出来,$28pts$,但是我错误的估计了我需要在 T2 上时所需的时间,因此在时间仅剩 10min 的时候掉头打了个暴力,然后还是错的。但是我并不知道,毕竟唯一一组可以跑的样例过了。
总体感想
很明显,这次在大的策略上出现了失误,错误的估计了我在 T2 和 T4 上所需的时间,导致二者失衡,最终在 T2 浪费了半小时有余,而并没有多得任何分。
和前面的人差距还是挺明显的,主要就是最后一题拉开了和我的差距。
24.7.18 赛后总结
题目
问题分析
T1
又是不用正解切题的一次。这次我真的什么别的也说不出来了,只能说个思路,复杂度不会分析。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr bool online=1;
int n,m,a,b,c,ans;bool dp[2][305][305][305],cn[2][5][7];
inline bool check(int a,int b,int c){
return (1ll<<c)+a*50+b*20<=100;
}
signed main(){
if(online)
freopen("horse.in","r",stdin),
freopen("horse.out","w",stdout);
ios::sync_with_stdio(0);
cin>>n>>m>>a>>b>>c;
dp[0][0][0][0]=1;
for(int di=0;di<=1;++di)
for(int dj=0;dj<=5;++dj)
for(int dk=0;dk<=6;++dk)
cn[di][dj][dk]=check(di,dj,dk);
for(int p=1;p<=n;++p){
memset(dp[p&1],0,sizeof dp[p&1]);
for(int i=0;i<=a&&i<=p;++i)
for(int j=0;j<=b&&j<=p*4;++j)
for(int k=0;k<=c&&k<=p*6;++k){
for(int di=0;di<=1&&di<=i;++di)
for(int dj=0;dj<=4&&dj<=j;++dj)
for(int dk=0;dk<=6&&dk<=k;++dk)
if(cn[di][dj][dk]&&dp[p-1&1][i-di][j-dj][k-dk]){
dp[p&1][i][j][k]=1; goto nxt;
}
nxt:
continue;
}
}
for(int i=0;i<=a;++i)
for(int j=0;j<=b;++j)
for(int k=0;k<=c;++k)
if(dp[n&1][i][j][k])
ans=max(ans,i+j+k);
cout<<ans<<endl;
return 0;
}
//exp:100
//请选手相信自己的程序的常数(悲)
//不在题面中说明,但是确实能跑过最大的数据
//复杂度:O(n*100^3*84),但是估多了,我也不知道多了多少
从最后的注释都可以知道我说不出来的原因。我是真的不知道这个程序的时间复杂度。我只能通过统计第 $29$ 行,那个 goto 的执行次数在最坏的情况下,输入为:150 300 100 100 100,会执行:101468747 次,运行时间稳定在 0.65s 左右。
思路很简单,首先,每匹马最多跑 $1$ 圈大圈,$4$ 圈小圈,以及过 $6$ 次河,而且三者不能同时成立。首先用贪心预处理出每匹马跑$0/1$ 个大圈,$0/\dots/4$ 个小圈,过 $0/\dots/6$ 次河可不可行。显然先过河。
然后,枚举每一匹马,利用上面推出的可行性暴力的枚举前 $p$ 匹马可不可以满足 $i$ 个大圈,$j$ 个小圈,过 $k$ 次河。显然有 $i\le p,j\le p\times4,k\le p\times6$。毕竟我们知道这个程序的复杂度真的很劣,能剪掉的状态必须剪掉。
这个状态显然只能由 $p=p-1$ 的状态推来,满足 $dp_{p-1,i^\prime,j^\prime,k^\prime}=1$,且令 $i=i^\prime+\Delta i,j=k^\prime+\Delta =j,k=k^\prime+\Delta k$,必须有一匹马能够跑 $\Delta i$ 次大圈,$\Delta j$ 次小圈,过 $\Delta k$ 次河。如果可行,就立即完全 break 掉,不再考虑他,因此使用 goto 跳出 $3$ 层循环。
这个复杂度我真的算不来。总之能过。
然而挂了十分。难受啊,枚举边界设错了,$i,j,k$ 应该枚举到 $0$,考场上只枚举到了 $1$。QAQ!
T2
很明显是被自己的思路和代码坑掉的一会。在代码的 $59$ 至 $67$ 行体现得极其明显:
for(int i=1;i<=n;++i){
int mp=0;
for(int j=1;j<=n;++j)
if(cn[j]>cn[mp]&&!chs[j])
mp=j;
if(!mp) break; chs[mp]=1;
for(int j=1;j<=n;++j)
if(bfvis[mp][j]) cn[j]--;
}//怎么看怎么像最小生成树
最后一句。说的确实没有错,但是这个思路的复杂度没有办法套到 $n$ 更大的范围内。事实上,我确实花了 $1h+$ 的时间把这个思路优化后放到了大数据内,但是实际情况是他会又超时又爆空间。根据代码 $111$ 行的批注,他在运行大样例时,用了 $10s-$ 和 $2GB+$。
发现自己的思路中所缺失的那一步真的太容易想到了:矛盾只会存在于两个不同的映射值之间(这里的映射值是指除去三次根后的数值),不会影响到第三个值。然而,我在意识到这一点后只用来更快的建出图,而没有意识到这个图不连通。
以及,这道题在洛谷上的数据是有问题的(7.18 18:00),待修复。问题是前四个点,输入个数不足,用快读就会出问题。
T3
好吧,这种字符串的题确实有一段时间没写过了,对这类题的熟练度和敏感度都降了不少,AC自动机,KMP就没有一个回想起来了的。
对这一题的策略也有问题。最后 $15$ 分钟了在那里拼命回想 KMP,打了代码放上去,最后几秒又换回了暴力。这想想都知道不合理,但是我就这么干了。赛后自测了一下,这两个程序就没有一个能拿分的。
最后几分钟真的不要乱动代码啊!好好跑一跑时间可以接受的大样例,万一有错还有机会修改。
题解给的哈希与根号分治的思路确实巧妙,%%%,复杂度足够通过此题了。
所以说,好好复习一下字符串吧(悲)。
T4
这道题就非常难受了,真就只有那特殊性质的 $10pts$,题解看了半天,还是一知半解的,想着结合一下 std,发现 std 整整四页。算了,假期找个时间再啃啃吧。
总体感想
这周以来发挥的相对最正常的一次,没有犯什么致命性的错误。虽然排名确实有点靠后。
很明显,遇到今天这种偏简单的题,还是要想办法啃一啃 T2 或者 T3 啥的才行。
24.7.16 赛后总结
修正
首先修一下分。T2 题意表述不明,依照正确的题意修正后能够拿 $70pts$,总分 $70$。
题目都是形式化后的,题解却没有形式化,T1 对不上号。
题目
问题分析
T1
很明显,这几场下来发现最大的问题就是像 T1 这样的题目总是想不出来,没有思路,或者莫名其妙的挂掉一些分。
吐槽一下,这次的数据太强了,一个有一定概率能做对的程序给卡成了零分。
其实说起来自己真的已经尽力了。最开始程序打出来,发现过不了大样例的时候就已经尽可能在找问题了,发现自己根本不会暴力,写了个暴力程序在那里对拍,拍出来暴力错了。能干的基本都干了,暴露出来的就只能是自己的能力问题了。
相比昨天,今天的心态都已经算是不错的了。
目前发现自己的代码的基本结论又错了。引用一段郝泽旭的代码的注释: //100 - (99 - (1 + 500) - (200 +500) - 200)。在我的代码里面,显然能够看出我并没有意识到中间再套一层括号可以使其更优。
正因为这一个问题,我的代码直接爆零了。当然了,这个问题做相应的修正之后就可以正确的切掉了。
T2
就这一句:“如果不联通,请输出 1000000000000000000”(单独成段)。当你读到这里你怎么想?图不连通就输出一个,然后结束;还是对于每一个点不连通的话就输出一个?总之,我理解到的是前者,题目的意思是后者。挂了 $70$,要求补分。
考场上没有犯什么致命性的错误,最终还是侥幸拿了个 $70$ 分,还算可以。这一题对我还是有比较大的参考价值的。基本上能拿的各种分都拿完了,而且时间控在了一个相对合理的范围。
但是,怎么说?又来!极值问题的转化。不过这一次在转化方面的思路上终于正确了一回:一个免费,一个两倍。
然后呢!!!都想到这个份上了,还想不到正解是什么鬼!
其实到也并不奇怪,毕竟分层图这玩意我平时确实基本就没有见过,在考场上想要想到还是有一定的难度的。不过,错一次就够了,下一次遇到分层图能够反应过来就好。
其实,仔细思考过题解的都知道这个做法正确性显然,只是多考虑了一些更劣的情况,不过时间复杂度没有那么高,完全可行。
T3
这题是真的没有一点思路。考场上打了一个 $O(n^2\log^2n\times n^n)$ 复杂度的暴力,连第一个点都过不了。
正解是DP,但是需要推式子,考场上真的推不出来一点。
T4
考场代码没拿分,符合预期,因为知道代码有一个没办法修补的漏洞,考场分配的时间也相对不多,可以接受。
然而,正解涉及到了后面再补的网络流,最小割等知识点,暂时改不了。
这道题就提到了分层图,T2 还是没想到 qwq。
总体感想
题越简单题越难,形式化完长度就一点,但是一点思路都没有。
这两场考试,我都犯了两个致命的决策性的错误:一是出现了大方向性的错误后没能及时调整;二是选择上交自己认为错误概率较小的错解。教训还是很惨痛的吧?上次 $20$,这次 $70$。
似乎还是昨天那句话,但是加两个字:能稳定拿分的才是王道。
24.7.15 赛后总结
题目
问题分析
这场比赛不能暴露出任何算法方面的问题,因为本场比赛的状态并不满足对上述方面进行考察的基本要求。
这次的难度简直离大谱,平均分才 75.5pts,像 T2 这种更是只有 1.17pts 的平均分。
其中,较为不常见也极为可惜的是:思路最接近正解的是 T3,而且和正解差别已经不大了。最终因出现了读题错误(不那么重要)和博弈的策略的细微错误(极为重要)而直接爆了零。
题目也是相当的炸裂。T4,可以引用之前的一句话:请选手相信自己程序的常数。$O(n^6),n\le70$ 的东西靠常数小卡过了。这常数算下来在 $10^{-3}$ 往下走。没有思考价值。
至于T1,因为没有样例解释,因此在第 $5$ 遍看题的时候才构造出了样例,并且将之前的研究T1的根基性的结论证伪了。
在这种情况下,考察的重点已经不在于算法之类的东西,而在于心态了。显然,这么一来,我心态早炸了。
还是对每道题做一个小总结吧。
T1
不用说了,最后一个小时才证伪了基本结论,这种情况下很难静下来思考,利用了一下 Subtask3 的特性骗了 20 走人。
T2
没有思路,调暴力,调了近一个小时没调通,心态再次爆炸。
T3
唯一一道有点思路的,错了那两个细节,爆零了。题解。
T4
$n=70$ 跑 $O(n^6)$ 的 DP,亏你出题人想得出来!!!
就考场思路而言的话,确实有想过类似的方法,但是时复“超了”,根本没敢写。
其实也不应该爆零,毕竟特殊性质摆着,按理说应该能够拿个20pts的,却没有拿,也是一个失误吧。
总体感想
太炸裂了。希望下次不要遇到,更希望下一次遇到类似的情况的时候冷静冷静再冷静,不要急躁,静下来把该拿的分给拿了。能拿分才是王道。
24.7.13 赛后总结
题目
问题分析
T1
考场上不知道在干什么,真的花了整整一个半小时去钻研各种“正解”,然而一无所获。我也不知道考场上究竟想了什么,总之真的一点思路都没有。
哎,总之死得很惨,只有 $40$ pts。没什么可总结的了。根本没有想到去往连续段的角度进行烧烤。
T2
真的怀疑自己又在发癫。考场上甚至想到了记忆化进行 $\log$ 级别的求解,结果却认为有数据可以把他卡到 $O(n)$,就果断放弃了去打暴力。
Em,解放思想,实事求是,不要想当然的下定论,特别是感觉接近正解的时候真的谨慎一点,不要随便对一个“提案”进行“表决”。
T3
确实抽象,想过两个东西分别按照不同的维度进行维护,但是属实没有想到怎么转化那个 $min$,比如做差的那一步。
这一点之前也出现并且总结过的,就是对这种极值问题的转化能力的极度的缺乏。
只能说如果后面还要再考的话多半也是个死,因为确实不会,等后面来补吧。
T4
数据不能说水吧,但是确实让错解拿到了太多分。
正解是可以左右横跳非常多次,但是我只让程序调了两次方向,即跳了 $3$ 次,就有了 $95$ pts,确实在我的意料之外。
Em,大胆尝试的实例化。
总体感想
总结写到这里,也看一看这一周都有哪些问题吧:
- 数学能力,包括推式子等(4)
- 概率相关的偏难的知识点的不了解(2)
- 对极值问题的转化(2)
- 对规律的敏感程度(1)
还是 7.11 那篇总结点到了关键:总是和正解数步之遥,然后做不出来。不局限于已有的框架。无论是思路,实现方式还是代码,全方位的解放。
解放思想,实事求是。
24.7.12 赛后总结
题目
问题分析
T1
又是不用正解切题的一次。
简单说一下我的思路吧。首先特判出 $a=1$ 的情况。这种情况会使我的代码更劣。因此等会儿另讲。
对于其他情况,在 $n\times(a-1)/a$ 到 $n$ 之间一定是独立的,可以直接加到答案里。剩下的部分暴力检查。
就这能不 TLE?先给代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr bool online=1;
int n,a,b; bitset<500000008>bt;
signed main(){
if(online)
freopen("rose.in","r",stdin),
freopen("rose.out","w",stdout);
ios::sync_with_stdio(0);
cin>>n>>a>>b;
if(a==1){
int ans=0;
for(int i=1;i<=b;++i){
int cnt=(n-i)/b+1;
ans+=(cnt+1)/2;
}
cout<<ans<<endl;
return 0;
}
int siz=n*(a-1)/a;
int lst=ceil(n*1.0/a);
for(int i=1;i<=lst;++i)
if(!bt[i])
if(i*a+b>n) siz++;
else if(i*a+b<lst) siz++,bt[i*a+b]=1;
cout<<siz<<endl;
return 0;
}
//exp:60~100
//理论上复杂度偏高,可能会超时
//实际上手造的极限数据它能在较优秀的时间内跑过
//只能估到这里,他的极限在 Subtask4 出现,期望0.5s
包括注释在内都是考场上的。这份代码的Hack应该很显然。1000000000 2 1,这样就会无一幸免,但是实测的话发现能够在 $0.6s$ 左右稳定的跑过。
中间的 $a=1$ 的特判也很好手推出来,就不做过多的讲解了。
比正解劣了不少,但是都是 $O(能过)$。
T2
数论简直菜成狗了,这几天的数学系统似乎直接宕机了。考场上连那一坨式子 $=\prod(\gcd(\dots)+1)$ 都没想到。
后面的对状态的压缩也非常的巧妙,将 $m^3$ 个状态压到了只剩 $m\log m$ 左右,确实难想。
还是自己的推式子的能力实在太弱了。
T3
还好,考场上把 $O(q\min(q,n^2))$ 的暴力打了出来,骗到 $50pts$。看一眼正解就知道问题主要出在哪里:不会较为高效的维护含有 $\min$ 的式子。
其实总结一下主要就是两种方法:转换法或者暴力法。要么将这个式子转换成不含 $\min/\max$ 的式子,要么去拿数据结构暴力维护。
T4
算了,$10pts$ 的暴力分拿了就走了吧,后面的什么错排数,光速幂啥的确实不知道,也不太会用,放一放吧。
总体感想
这次的问题核心在 T2 上:能拿分却没拿到,导致分数不那么的高了。还是要尽量的多拿分,衡量好每道题到底花多少时间能尽量得到更多的分。
24.7.11 赛后总结
题目
问题分析
T1
额,又挂了些分。是一个取等条件。按理说能取的全部都要取,但是实际上我只取了大于零的情况,可是等于零的也能取。
难受至极,被捆走 $30$ pts。
怎么说呢?确实是自己的问题,不能归为粗心大意了,因为我看完了 Hack 后仍然认为我没有错,运行完才知道哪里出了问题。
只能说下次尽可能不犯了。
T2
推式子的能力太弱了啊啊啊啊啊…
考场上都已经推到两个前缀和了都没想到再拆一下。属实人才。
再仔细看一看题解的后面,发现自己简直是正解描边大师。Subtask2 的前缀和想到了,Subtask3,5的待定系数也想到了,Subtask4的不会预处理的情况也想过,总之就是头绪全都想得到,正解的三不沾。
无论怎么说,反正是不太想得到。一定要做一个更高层次的总述的话,那就是深度思考的能力有待提高。依然是“菜就多练”。
T3
可以说,这是思路相对最接近正解的一题(抛开T1)。从代码末尾的注释可见我将前两个 Subtask 写了出来,并且明确知道正解会是怎样的,但是我始终没有想到怎样在一开始的时候快速的求两两的距离之和。
很好,题解中用另一种方法间接的求出了这个和。心里十分的崩溃,和满分就是一步之遥。
T4
额,考场上真的啥别的也想不到,这玩意也就线段树能够暴力维护了吧,然后拿了这 $70$ 分。看完题解直接人都傻了:谁没事想分块啊!
总体感想
总的来看这几次考试,发现一个长期以来一直通用的规律:总是和正解数步之遥,然后做不出来。
解放思想,实事求是。所以说,我需要突破的无非就是不局限于已有的框架。无论是思路,实现方式还是代码,全方位的解放。
24.7.10 赛后总结
题目
online judge
问题分析
T1
莫名其妙的挂了 $20$ 分,事后发现少了一个特判,导致有且仅有一个点不能过,然后因为捆绑而集体掉分。
要说教训的话,就是不要乱删已有的表。这些东西在有了“疑似”正解后可能显得很不必要,但是他能在你的正解出现一些未知的错误的时候尽可能地帮你减少一些损失。
出现 WA 的那个点对应的表我是打过的,但是有了“正解”后就把他删了,毕竟样例中没有对应数据,我也没注意到这个问题。
T2
又是不用正解切题的一次,有的点快要跑上一秒,有的点又比 STD 快不少。
其实赛时就已经注意到了其复杂度的问题,理论上最高能够跑到 $O(n^2\log m)$,连 Subtask4 都很难跑过,但是他连最大的样例都能在一个较为优秀的时间内跑过。
事已至此,几乎只能够祈祷数据随机生成了。我的方法是这样的:
搜索,标记。用我最爱用的优先队列 BFS,记录三维:时间,地点,答案所求值。然后队列中以答案所求值为第一关键字,时间为第二关键字写比较函数。然后就是搜索。
至此,已经很像最短路了。标记也是两维,第一维是位置,第二维是时间。不能够只记录一维,因为涉及乘法,前面更小的在后面可能会更大。再小小的剪一个枝:一直转圈一定不优,因此限制时间的值 $\le n$。
但是,问题也很明显:这东西不时空双爆才怪!特别是空间,两维,每维都是 $n$,用 $bitset$ 都卡不过!
这也是本代码最有赌的成分了:我都他每一个节点被到达的次数都不会多,也就是说记录空间有浪费。因此,我在二者都十分紧张的情况下选择了空间换时间:时间的标记使用 unordered_set 维护。
可以说就这么赌中了 $100$ pts。当然也不奇怪,这种思路很多人一开始就会淘汰掉,或者只用来拿暴力分,数组开小,多数情况下出题人不太会去卡这种解法。
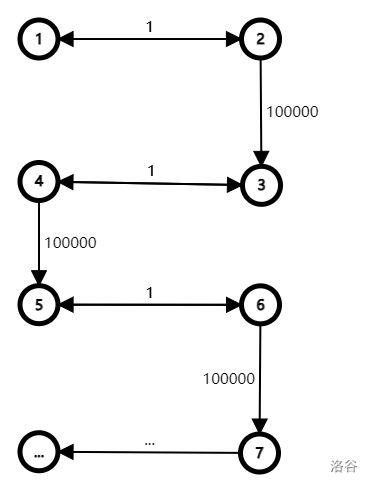
当然,还是声明一下这个解法并不是正解,他也有 hack,如下图:
那么对应到我的代码当中的时候,特别是前面部分会由于边权足够小而卡满时间标记。
顺带提出一种修补的办法:在每一个节点维护一个类似于单调栈的结构,核心思路就是如果有一个做法答案值比你小,时间还比你早,那你就可以废了。
虽然看起来维护难度有上升,但是能够防住上面所提供的 Hack。如果暂时抛开维护这个标记的时间复杂度,那么其最坏复杂度应该能够降到 $O(n\log\log n\log m)$,约为 $2.28e7$,理论上完全能够降到时限 $3s$ 以下。当然了,上面的时间复杂度只是直觉,也有可能更优,但是能保证在 $O(n\log n\log m)$ 以下。
给一份考场代码吧:
#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr bool online=1;
struct node{
int p,v;
node(int pi=0,int vi=0):p(pi),v(vi){}
}; vector<node>son[300005];
struct fode{
int p,t,mx;
fode(int pi=0,int ti=0,int mi=0):
p(pi),t(ti),mx(mi){}
friend bool operator<(const fode&l,const fode&r){
return (l.mx!=r.mx?l.mx>r.mx:l.t>r.t);
}
}tmp;priority_queue<fode>pq;
int n,m; unordered_set<int>vis[300002];
signed main(){
if(online)
freopen("b.in","r",stdin),
freopen("b.out","w",stdout);
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1,a,b,c;i<=m;++i){
cin>>a>>b>>c;
if(a!=b) son[a].emplace_back(node(b,c));
}
pq.push(fode(1,1,0));
while(pq.size()){
tmp=pq.top(),pq.pop();
if(tmp.t>n) continue;
if(vis[tmp.p].count(tmp.t))continue;
vis[tmp.p].insert(tmp.t);
if(tmp.p==n){
cout<<tmp.mx<<endl;
return 0;
}
for(int i=0;i!=son[tmp.p].size();++i)
if(!vis[son[tmp.p][i].p].count(tmp.t+1))
pq.push(fode(son[tmp.p][i].p,tmp.t+1,max(tmp.mx,tmp.t*son[tmp.p][i].v)));
}
return 0;
}
//exp:60~90
大致就是这样。这能告诉我们的就是:勇于尝试。如果你的程序能够保证不会在小数据点因改动而出现问题,那就尽可能地把范围改大。
T3
考场上显然是没什么思路的,只有打了个 $O(n2^m)$ 的暴力走人。考场上还是关注了表格的最后一项的,但是什么规律都没有发现。包括对中间的那一串树形的数据也有一定的思考,并尝试过打代码,但是都没能够成功。
就题解里面第一句得出结论,观察能力不够。至于后面的翻转相关的贪心及其维护那更是没有想到的。
总的说,能突破的就是昨天有所提及的直觉,以及靠打表发现一些规律的习惯。
T4
考场上没有注意到面积的并意味着哪怕和不同的长方形在同一个地方重叠也只算一次,愉快的爆 $0$ 了。
理解到了题意后再看,发现依然没有一点思路,只打了个 $O(n+m+rq)$ 的暴力拿走考场上可能可以拿走的分。
正解大概是调不出来了吧,又是可持久化的扫描线,又是询问标记永久化啥的,看着题解都懵,再瞅一眼STD直接整个人都不好了,只有不了了之。
还是有可以改进的地方:只要程序复杂度不是太大,还是尽量跑一跑大一点的数据,没准可以发现对题意理解有误。
总体感想
发挥的还算可以了,预估的是 $100+[60,90]+20+5=[185,215]$,实际有 $80+100+25+0=205$,可以接受。
还是有教训的。盼君勿忘。
24.7.9 赛后总结
题目
online judge
问题分析
T1
没什么问题,赛时 AC,并总结出经验:打完暴力后用暴力打个表,可能会发现规律。
T2
很明显,对概率,特别是非经典概率,即情况有无数多种的无论是从了解,代码熟悉程度还是到应用都不足。
考场上看到这道题的时候立马知道了思路:列方程,然后使用高斯消元进行求解($60$ pts)。但是,因为相关的题见的远远不够多,连方程都不会列。当场死亡,连 $n,m\le2$ 的表都打不完整。
下来后还发现了另一个问题:考场上我是在按照正向进行推方程,但是因为后面的会覆盖前面的,因此思考了一会后毅然决然地选择了放弃。
从中主要反映出了我对概率这一个大板块的不熟悉。包括但不限于对对概率和期望的求解方向的灵活变通,以及对期望的后效性的处理的极端的不熟悉,需要一定的加强。
T3
算了,好像有一点点超纲了,题解中似乎涉及了一种名为等价类的东西,正解中更是需要用到动态构建等价类什么的高级东西,改不了一点,先放着吧。
还是有一点的小问题:考场上过于犹豫,同一个功能拿不同方式反复实现了两三遍。没事别这么干。
T4
额,不知道怎么说了。题面里有一个“如果你采用最优的策略”。我怎么知道什么是最优策略?考场上大致猜了个结论,然后代码写出来调了调,能过第一个样例,但是别的都没过。当时只剩 $6$ 分钟了,不敢动了,还是交了上去,直接爆零。
最后知道了,策略都错了,时间也没留够,没有时间去验证。
可以突破的地方可能就是在时间不太足够的情况下的直觉的准确性。
总体感想
难度偏高了(引用视频题解),当然,正常发挥时该拿的分还是差不多拿了。主要的问题就是对概率的理解与运用吧。加强练习,菜就多练!
24.7.8 赛后总结
题目
问题分析
T1
这一题的核心思路是“分别计算每一项的期望”。其实这一点也并非没有想过,但是当时停留在了求 $s$ 上而非求 $s^2$ 上,这就导致我认为其无法使用二进制拆分进行求解的关键。
后来翻阅了题解后我已经知道了 $(s_{29}+s_{28}+\dots+s_0)^2$ 这个东西可以拆开成为许多的 $s_is_j2^{i+j}$。我并非不知道,但是考场上确实没能静下来深究这一点。而这就是我所需要突破的地方之一:对数学式子的深度的了解和灵活的运用与变通。
到了这里,才只完成了第一步。还有一点需要突破:$s_is_j$ 的求值。
很显然是通过 DP,但是转移仍然困难。其中还有另外的极为巧妙的一步:求其中选取了奇数个或者偶数个的概率。
他每一次算“概率”时都算的是 $1$ 减去两倍被选择的概率,最后再拿 $1$ 加减整体。整体展开后正是所求。
这个地方本质上还是上述的突破点,只不过这个远比上面的更难想到。不利用这一点多开一维进行求解也可以卡过。先达成上面所述的数学水平再说吧。
T2
题解说的第一点:恰好难处理,就处理前缀和考场上已经想到了,并依靠这一点拿了前 $40$ 加上后面一个比较水的点的 $5$ 分。
但是,题解中更关键的一步:容斥,在考场上并没能想到。最开始我们将序列的填数问题变相的转化为了数的拆分问题,而这的典型方法就是插板法。
容斥在哪里呢?因为他会有一定的限制,所以需要将不合法的情况全部排除掉,在这一步会用到,而我们仍然会用到插板法。
最后,由于题目的特殊性质,钦定的数的个数过大的时候一定无解,所以复杂度为调和级数,可过。
那么需要突破的地方也无非就是对题目的模型的抽象化,也就是所谓的形式化。这个能力可以在一定程度上降低题目的难度。其次就是对容斥的运用的熟练程度。而根据这道题,很显然这个熟练度是远远不够的。
T3
这题没什么好说的,死了就是死了,考场上连 $O(n)$ 求解特定区间的方法都没能正确的找到,更别说把这道题给做出来了。
最开始的时候,我想当然的推了一个式子出来,然而他是错的,我也并没有发现,知道打完线段树开始调试了才猛然发现。
好歹发现了,但是后面并没能够静下来重新推式子,错失中间的 $40$ 分。
而正解也是基于线性求解区间答案的方法基础之上的。我们会需要利用栈的大小,转化为胜者。
到这里,已经十分考验能力了。就个人感受,如果当时能够静下来,可能也只是能够推出线性求解的方法来,要做出这道题还远远谈不上 。
后面的方法也只是一些维护技巧了,对于不同的题目并不具有太强的可迁移性。然而仍有可突破的地方。
主要是对心态的调整。这一点看总体感想。
T4
这题有点超纲了,暂时抛开不谈。把前20pts拿了就行了。
总体感想
这套题的难度确实远比以前高。做这些题的时候已经不是很能够直接看出什么算法了。
这一次的一个较为重大的问题就是心态。第一题一来没看懂,本身还好。第二题打了个没有仔细想过的 DP,然后也错了,到第三题更是直接没想什么就打了个线段树,然后还是错的。看了眼第四题题都没看懂。
就这种情况之前其实并没有遇到过,但也正因如此才会需要突破。遇到题目首先就是不要慌,稳住阵脚,静下来仔细思考,动用好自己已知的知识尽可能地获得多的分数。特别是三四题。难度本身就不小,不要去试错,浪费时间还及其影响心态。
总之,$4$ 个小时真的不算短,冷静沉着,深度思考才是硬道理。