浅谈数学——从折叠板子题学七种解法

# 前言
昨天写了一篇博客加 rp，今天 Thupc2024 烧鸡了，明天月考，再写一篇，rp++。

# 引入

这是一道折叠的模板题。

如图所示，$AC=3, BC=4, \angle CAB=90\degree$。点 $D$ 是线段 $AC$ 上的一个动点，将 $\triangle ADB$ 沿 $AD$ 折叠到 $\triangle A'DB$，使 $A'$ 落在 $BC$ 边上。求 $AD$ 的长度。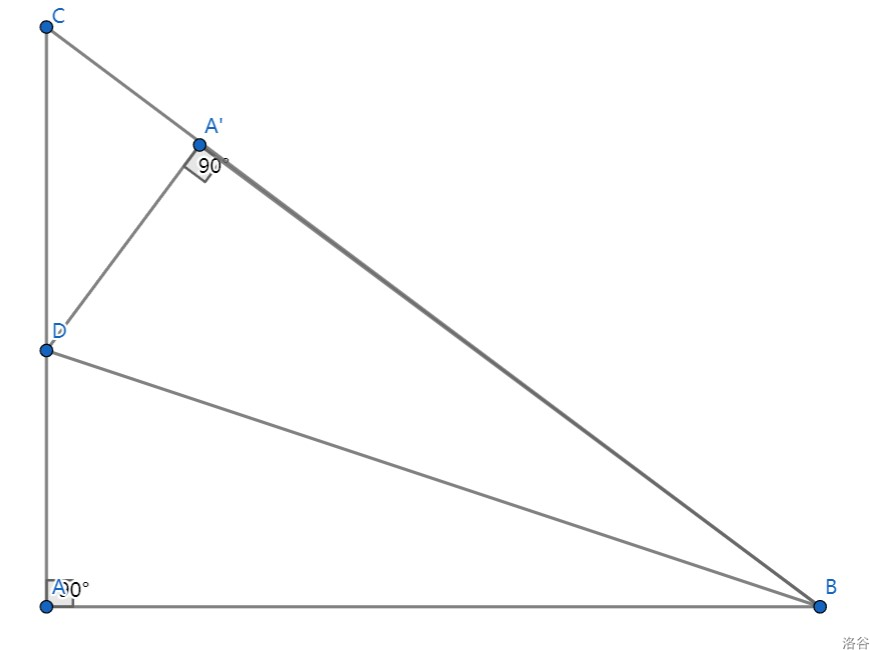

![](https://cdn.luogu.com.cn/upload/image_hosting/bseexq2m.png)

## 解法 1: 勾股方程

前置知识：勾股定理。

> 折叠的本质，就是找非重叠部分列勾股方程。——我的数学老师

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree$，  
由勾股定理得 $BC=\sqrt{AB^2+AC^2}=5$。

由折叠知：$A'B=AB=4, A'D=AD, \angle DA'B=\angle DAB=90 \degree$。

$\therefore A'C=BC-A'B=5-4=1, \angle DA'C=180 \degree-\angle DA'B=180\degree-90 \degree=90 \degree$。

设 $AD=A'D=x$，则 $CD=AC-AD=3-x$。

在 $Rt\triangle A'CD$ 中，$\angle DA'C=90\degree$，  
由勾股定理得 $A'C^2+A'D^2=CD^2$。

即 $1^2+x^2=(3-x)^2$，解得 $x=\dfrac{4}{3}$。

所以 $AD=\dfrac{4}{3}$。

## 解法 2: 特殊角科技之一

前置知识：[特殊角科技](https://www.luogu.com.cn/blog/stripe-python/the-magic-37-degree)。

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree$，  
由勾股定理得 $BC=\sqrt{AB^2+AC^2}=5$。

由折叠知：$A'B=AB=4, AD=A'D, \angle DA'B=\angle DAB=90 \degree$。

$\therefore A'C=BC-A'B=5-4=1, \angle DA'C=180 \degree-\angle DA'B=180\degree-90 \degree=90 \degree$。

在 $Rt\triangle ABC$ 中，$AC:AB:BC=3:4:5$

$\therefore \angle DCA'=53 \degree$

$\therefore \dfrac{A'C}{A'D}=\dfrac{3}{4}$

$\therefore A'D=\dfrac{4}{3}$

$\therefore AD=A'D=\dfrac{4}{3}$

## 解法 3: 相似
~~这才是特殊角的本质。~~

前置知识：相似三角形。

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree$，  
由勾股定理得 $BC=\sqrt{AB^2+AC^2}=5$。

由折叠知：$A'B=AB=4, AD=A'D, \angle DA'B=\angle DAB=90 \degree$。

$\therefore A'C=BC-A'B=5-4=1, \angle DA'C=180 \degree-\angle DA'B=180\degree-90 \degree=90 \degree$。

在 $\triangle ABC$ 与 $\triangle A'BD$ 中：

$\because \angle CAB=\angle CA'D = 90\degree, \angle C=\angle C $

$\therefore \triangle ABC \sim \triangle A'BC$

$\therefore \dfrac{A'C}{A'D}=\dfrac{AC}{AB}=\dfrac{3}{4}$

$\therefore A'D=\dfrac{4}{3}$

$\therefore AD=A'D=\dfrac{4}{3}$

## 解法 4: 建系

前置知识：平面直角坐标系。

解：以点 $A$ 为原点，$\dfrac{1}{3}AC$ 长为单位长度建立平面直角坐标系，如图：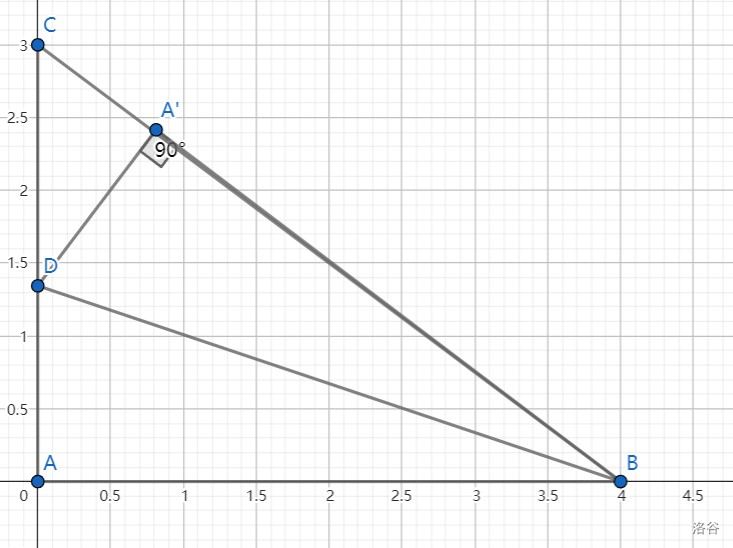

![](https://cdn.luogu.com.cn/upload/image_hosting/uq1j0kus.png)

$\therefore B(4,0), C(0,3)$

设 $BC: y=kx+b(k\ne0)$。

将 $B(4,0)$ 与 $C(0,3)$ 代入 $y=kx+b$ 中得：

$$
\left\{\begin{matrix}4x+b=0
 \\b=3

\end{matrix}\right.
$$

解得

$$
\left\{\begin{matrix}x=-\dfrac{3}{4}
 \\b=3

\end{matrix}\right.
$$

由折叠知：$A'D=AD, \angle DA'B=\angle DAB=90 \degree$

设 $D(0,y)$。

$\therefore DA'=DA=y$

即 $\dfrac{|3-y|}{\sqrt{1+(-\dfrac{3}{4})^2}}=y$

解得 $y_1=\dfrac{4}{3}, y_2=-\dfrac{4}{3} \text{(舍)}$

$\therefore DA=y=\dfrac{4}{3}$

## 解法 5: 四点共圆，割线定理

前置知识：四点共圆 & 割线定理。

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree$，  
由勾股定理得 $BC=\sqrt{AB^2+AC^2}=5$。

由折叠知：$A'B=AB=4, AD=A'D, \angle DA'B=\angle DAB=90 \degree$。

$\therefore \angle DA'B +\angle DAB=90 \degree+90 \degree=180\degree$

$\therefore A', D, A, B \text{四点共圆}$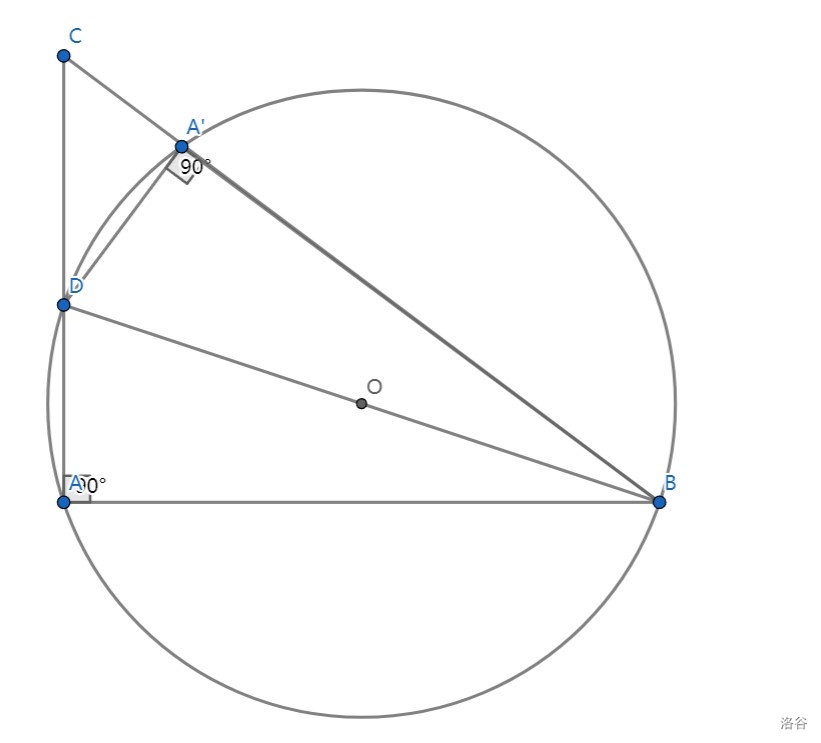

![](https://cdn.luogu.com.cn/upload/image_hosting/31fo1rtw.png)

$\therefore AC \times CD=BC \times A'C$

即 $3CD=5(5-4)$

$\therefore CD=\dfrac{5}{3}$

$\therefore AD=AC-CD=3-\dfrac{5}{3}=\dfrac{4}{3}$

## 解法 6: 角平分线定理

前置知识：角平分线定理 & 分式方程。

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree$，  
由勾股定理得 $BC=\sqrt{AB^2+AC^2}=5$。

由折叠知：$\angle DBC=\angle DBA$

$\therefore \dfrac{BC}{AB}=\dfrac{CD}{AD}$

设 $AD=x$，则 $CD=AC-AD=3-x$

即 $\dfrac{3-x}{x}=\dfrac{5}{4}$

解得 $x=\dfrac{4}{3}$，经检验是原方程的解。

所以 $AD=\dfrac{4}{3}$

## 解法 7: 特殊角科技之二

前置知识：[特殊角科技](https://www.luogu.com.cn/blog/stripe-python/the-magic-37-degree)。

我认为的最简方法之一。本质是半角公式。

解：在 $Rt\triangle ABC$ 中，$\angle CAB=90\degree, AB=4, AC=3$   
$\therefore \angle CBA=37 \degree$

由折叠知：$\angle A'BD=\dfrac{1}{2}\angle CBA=18.5 \degree, A'B=AB=4, AD=A'D$

在 $Rt\triangle DA'B$ 中，$\angle DA'B=90\degree, \angle A'BD=18.5 \degree$   
$\therefore \angle CBA=37 \degree$

所以 $\dfrac{A'D}{A'B}=\dfrac{1}{3}$

所以 $AD=A'D=\dfrac{4}{3}$

正在渲染内容...