线段树 - 洛谷保存站

## 线段树

线段树是一种数据结构，支持区间、单点修改，区间查询。

线段树是用一个段一个段的答案拼起来的，也就是说线段树是一个分治模型，每一个段表示一个区间：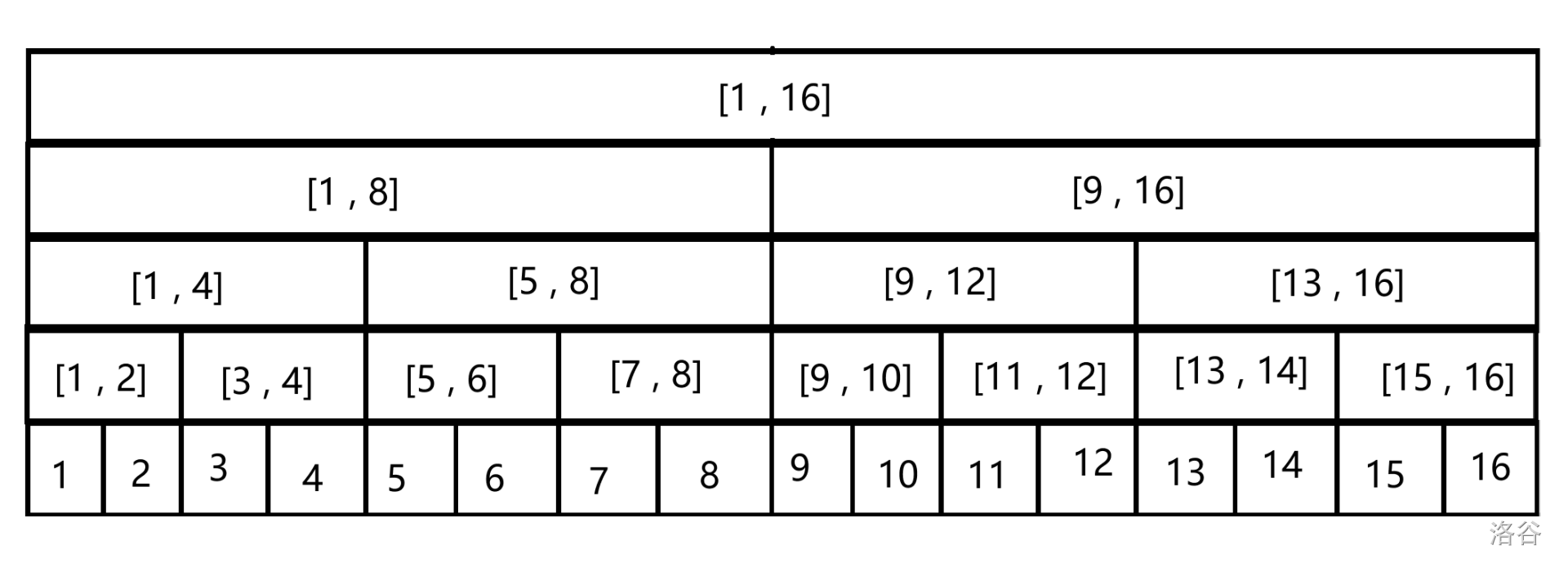

![](https://cdn.luogu.com.cn/upload/image_hosting/p1shtlm6.png)

这里每一个格子都会向下拆分，直到长度只有 $1$ 的时候才会停止拆分，此时的答案就是当前的节点（随题目变化）。

因为线段树可以看成是一棵二叉树，所以，当前节点 $u$ 的左儿子（左区间）就是 $u \times 2$，右儿子（右区间）就是 $u \times 2 + 1$，这是通过数组的方式对二叉树进行储存。

我们可以使用一个结构体储存当前节点的各个信息：区间左端点，区间右端点，区间的答案。

此时如果要查询区间 $[3 , 6]$，那么先从 $[1 , 16]$ 递归；发现区间被左边包含，此时递归 $[1 , 8]$；发现两边都有；先递归左边，来到 $[1 , 4]$；在右边，此时 $[3 , 4]$ 已被 $[3 , 6]$ 完全包含，不继续递归，返回区间答案；递归 $[5 , 8]$，在左边，$[5 , 6]$ 完全包含，返回答案。

这就是线段树的查询。

既然区间查询已经实现了，接下来是 **单点修改**。

我们直接递归找到这个点修改即可。

但是修改完了以后，还是不能让大区间修改，所以我们还要自底向上和并，也就是 `PushUp` 操作。

那么，如果是统计区间和的话，就是这样：

```cpp
void PushUp(int u) {
  tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum; // u << 1 等价 u * 2，u << 1 | 1 等价 u * 2 + 1，但是位运算会更快
}
```

将当前节点的和变为两个子区间的和，也就是更新。统计最大值就改成取最大值，最小值等同理。

但是你线段树都没建，怎么修改查询？

所以，我们还需要建树。

如果要建树的话，就记录当前节点，建树的区间，每次将当前节点的信息修改，即设置左右端点（传的参数），如果已经分到了最下面的话，那么还要设置答案信息。

注意建树的时候要向上合并！

那么，建树、修改和查询都完成了，看看这个 **单点修改**，**区间查询**。~~这不是树状数组吗？~~

还有，线段树的数组初始要开四倍空间，因为线段树存的是一个区间，一个二叉树可能是挂不满的。所以对于 $n$ 个点，比 $n$ 大的最小二次幂即为底层节点数，则所有节点数为：$2 ^ {\lfloor \log_2 n \rfloor + 1} \times 2 - 1$，即为接近 $4n$。

### [Luogu - P3374](https://www.luogu.com.cn/problem/P3374)

依次写出向上合并、建树、单点修改、区间查询即可，具体见代码注释。

### Code

```cpp
#include <bits/stdc++.h>
#define int long long

using namespace std;

const int kN = 5e5 + 1;
int n, m, a[kN];

struct Node {
  int l, r, sum; // 线段树信息
} tree[kN << 2];

void PushUp(int u) {
  tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum; // 向上合并区间和
}

void Build(int u, int l, int r) { // 当前为 u，区间的左右端点为 l 和 r
  tree[u] = {l, r}; // 存储区间信息
  if (l == r) {
    tree[u].sum = a[l]; // 已经到了长度为 1 的了，直接记录答案
    return; // 长度为 1，结束
  }
  int mid = l + r >> 1; // 找到区间的分界
  Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r); // 递归左右子树
  PushUp(u); // 建树更新完了，记得 PushUp！！！
}

void Update(int u, int p, int x) { // 当前为 u，将 p 号元素加上 x
  if (tree[u].l == p && tree[u].r == p) { // 到了修改的地方
    tree[u].sum += x; // 修改
    return; // 找到了，结束
  }
  int mid = tree[u].l + tree[u].r >> 1; // 找到区间的分界
  if (p <= mid) { // 如果点在左边
    Update(u << 1, p, x); // 递归左子树
  }
  if (mid < p) { // 点在右边
    Update(u << 1 | 1, p, x); // 递归右子树
  }
  PushUp(u); // 向上合并
}

int Query(int u, int l, int r)  { // 当前在 u，查询区间 [l , r] 的和
  if (l <= tree[u].l && tree[u].r <= r) { // 如果完全包含，直接返回答案
    return tree[u].sum; // 完全包含，返回
  }
  int mid = tree[u].l + tree[u].r >> 1; // 找到区间的分界
  int Sum = 0; // 记录和
  if (l <= mid) { // 左子树包含查询区间
    Sum += Query(u << 1, l, r); // 加上左子树的答案
  }
  if (mid < r) { // 右子树包含查询区间
    Sum += Query(u << 1 | 1, l, r); // 加上右子树答案
  }
  return Sum; // 返回最终答案
}

signed main() {
  cin.tie(0)->sync_with_stdio(false);
  cin >> n >> m; // 输入
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  Build(1, 1, n); // 建树
  for (int op, x, y; m--;) {
    cin >> op >> x >> y; // 输入
    if (op == 1) { // 修改操作
      Update(1, x, y);
    } else {
      cout << Query(1, x, y) << '\n'; // 查询操作
    }
  }
  return 0;
}
```

### [Luogu - P4392](https://www.luogu.com.cn/problem/P4392)

一道非常简单的题，只有查询操作，当作练手吧。

### Code

```cpp
#include <bits/stdc++.h>
#define int long long

using namespace std;

const int kN = 1e6 + 1, kI = 1e18;
int n, m, c, a[kN];

struct Node {
  int l, r, mx, mn;
} tree[kN << 2];

void PushUp(int u) {
  tree[u].mx = max(tree[u << 1].mx, tree[u << 1 | 1].mx); // 需要求解最大值和最小值
  tree[u].mn = min(tree[u << 1].mn, tree[u << 1 | 1].mn);
}

void Build(int u, int l, int r) { // 建树
  tree[u] = {l, r, -kI, kI};
  if (l == r) {
    tree[u].mn = tree[u].mx = a[l];
    return;
  }
  int mid = l + r >> 1;
  Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
  PushUp(u);
}

int Query(int u, int l, int r, bool f) { // f = 0 是求最小值，否则是求最大值
  if (l <= tree[u].l && tree[u].r <= r) {
    return (f ? tree[u].mx : tree[u].mn); // 返回答案
  }
  int mid = tree[u].l + tree[u].r >> 1, ans = (f ? -kI : kI);
  if (f) { // 求最大值
    if (l <= mid) {
      ans = max(ans, Query(u << 1, l, r, f)); // 递归
    }
    if (mid < r) {
      ans = max(ans, Query(u << 1 | 1, l, r, f));
    }
  } else {
    if (l <= mid) {
      ans = min(ans, Query(u << 1, l, r, f)); // 递归
    }
    if (mid < r) {
      ans = min(ans, Query(u << 1 | 1, l, r, f));
    }
  }
  return ans; // 返回答案
}

signed main() {
  cin.tie(0)->sync_with_stdio(false);
  cin >> n >> m >> c;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  Build(1, 1, n); // 建树
  bool f = 0;
  for (int i = 1, r; i <= n; i++) {
    r = i + m - 1; // 右端点
    if (r > n) { // 保证 r <= n
      break;
    }
    if (Query(1, i, r, 1) - Query(1, i, r, 0) <= c) { // 判断是否满足条件
      cout << i << '\n';
      f = 1;
    }
  }
  cout << (!f ? "NONE" : ""); // 如果没有答案，输出 NONE
  return 0;
}
```

### [Luogu - P3372](https://www.luogu.com.cn/problem/P3372)

这题就变成了区间修改，如果还是一个一个地找到底层修改，修改的时间复杂度就和暴力一样了。所以，我们需要优化。

### 区间修改优化

我们可以添加一个标记，叫做懒标记（`lazy_tag`），或延迟标记（`delay_tag`）。

这个标记和我们平常用的浏览器比较类似，因为平常的浏览器如果有一个页面长时间未访问，就会设置为睡眠状态，只有访问的时候重新加载。

这个标记也一样，只有查询和修改到这个点的时候才修改。

因为懒标记肯定是要下发的，所以这个标记的更新是自顶向下，所以要在递归之前进行修改：

```cpp
void PushUp(int u) { // 对 u 进行向下更新
  if (tree[u].tag) { // 如果当前的标记存在才会下发
    tree[u << 1].tag += tree[u].tag, tree[u << 1].sum += (tree[u << 1].r - tree[u << 1].l + 1) * tree[u].tag; // 下发标记给左儿子，同时更新区间和
    tree[u << 1 | 1].tag += tree[u].tag, tree[u << 1 | 1].sum += (tree[u << 1 | 1].r - tree[u << 1 | 1].l + 1) * tree[u].tag; // 同理，下发给右儿子
    tree[u].tag = 0; // 记得要清空标记！
  }
}
```

那么，在完全包含修改区间的时候，$tag$ 也要加上题目所加上的值，因为还要传下去，同时还要将当前的值加上长度乘加上的值，进行更新。

在查询的时候也要加上下发。

### Code

```cpp
#include <bits/stdc++.h>
#define int long long

using namespace std;

const int kN = 1e6 + 5;

int n, m, a[kN];

struct Node { // 线段树信息
  int l, r;
  int sum, tag; 
} tree[kN << 2];

void PushUp(int u) {
  tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum; // 向上合并
}

void PushDown(int u) {
  if (tree[u].tag) { // 是否下发
    tree[u << 1].tag += tree[u].tag, tree[u << 1].sum += (tree[u << 1].r - tree[u << 1].l + 1) * tree[u].tag; // 下发给左儿子
    tree[u << 1 | 1].tag += tree[u].tag, tree[u << 1 | 1].sum += (tree[u << 1 | 1].r - tree[u << 1 | 1].l + 1) * tree[u].tag; // 下发给右儿子
    tree[u].tag = 0; // 清空标记
  }
}

void Build(int u, int l, int r) { // 建树
  if (l == r) {
    tree[u] = {l, r, a[l]};
    return;
  }
  tree[u] = {l, r};
  int mid = l + r >> 1;
  Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
  PushUp(u);
}

void Update(int u, int l, int r, int k) { // 更新，区间 [l , r] 加上 k
  if (l <= tree[u].l && tree[u].r <= r) { // 完全包含
    tree[u].tag += k; // 修改懒标记
    tree[u].sum += (tree[u].r - tree[u].l + 1) * k; // 修改和
    return;
  }
  PushDown(u); // 向下发放
  int mid = tree[u].l + tree[u].r >> 1;
  if (l <= mid) {
    Update(u << 1, l, r, k); // 递归
  }
  if (mid < r) {
    Update(u << 1 | 1, l, r, k);
  }
  PushUp(u); // 向上合并
}

int Query(int u, int l, int r) { // 查询
  if (l <= tree[u].l && tree[u].r <= r) { // 完全包含
    return tree[u].sum;
  }
  PushDown(u); // 下发
  int mid = tree[u].l + tree[u].r >> 1;
  int Sum = 0;
  if (l <= mid) {
    Sum += Query(u << 1, l, r); // 递归
  }
  if (mid < r) {
    Sum += Query(u << 1 | 1, l, r);
  }
  PushUp(u); // 合并
  return Sum;
}

signed main() {
  cin.tie(0)->sync_with_stdio(false);
  cin >> n >> m;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  Build(1, 1, n); // 建树
  for (int op, x, y, k; m--;) {
    cin >> op >> x >> y;
    if (op == 1) {
      cin >> k;
      Update(1, x, y, k); // 修改
    } else {
      cout << Query(1, x, y) << '\n'; // 查询
    }
  }
  return 0;
}
```

## The End.

正在渲染内容...