主页
搜索
最近更新
数据统计
赞助我们
申请密钥
系统公告
1
/
1
请查看完所有公告
学习笔记——Trie树(字典树)
最后更新于 2025-07-01 18:18:46
作者
WJX3078
分类
算法·理论
复制 Markdown
查看原文
删除文章
更新内容
# 1.字符串$Trie$ > $Trie$树(字典树)是一种用于实现字符串快速检索的多叉树结构。$Trie$树的每个节点都拥有若干个字符指针,若在插入或检索字符串时扫描到一个字符$c$,就沿着当前节点的$c$字符指针,走向该指针指向的节点。 --《算法竞赛进阶指南》 光看$Trie$树的定义,感觉它太过抽象了,根本不好理解,所以我们图文结合学习$Trie$树。 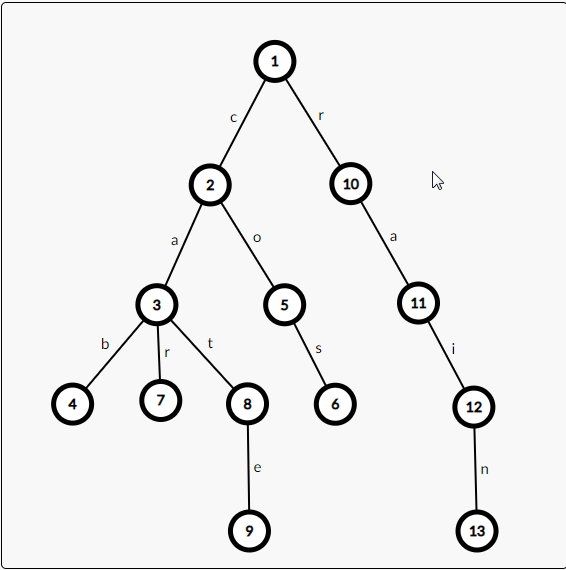 如上图所示,我们依次在该字典树中插入`cab`、`cos`、`car`、`cat`、`cate`、`rain`等字符串,得到的就是上图的字典树。 我们观察发现,对于有相同前缀的字符串,从$Trie$树根节点一直走到第一个不相同字符的节点,再由该节点新连一条到新建字符节点的边,就可以完成一个新字符串的插入。 细心的$OIer$可能已经发现了问题:我怎么知道一个字符串走到哪算结束? 就像上图中的字符串`cat`和`cate`,如果我们从根节点一直走到叶子节点的话,显然会错过`cat`节点,那我们就再开一个数组记录该节点是否为一个字符串的结束节点,这样就可以保证检索时不会错过任何一个字符串。(在上图中,$end[4]=end[6]=end[7]=end[8]=end[9]=end[13]=1$)。 显然,这样$Trie$树的空间复杂度十分大,一般来说,我们在树的边上保存字符,在节点处保存一些额外信息,这样其空间复杂度就是$O(NC)$,其中$N$是节点个数(最长字符串长度$\times$总字符串数),$C$是字符集大小。 接下来就直接上代码了: ```cpp int trie[SIZE][26],tot=1;//SIZE大小视题目而定,tot记录新建节点的编号 //这里是默认只有26个字符,看题目字符集大小来真正确定 //SIZE表示字符串的总长度 bool end[SIZE];//要保证每个节点都有,所以大小为SIZE*26 il void insert(char *str) {//插入一个新字符串 int id=1,len=strlen(str+1);//默认字符串从1开始输入 for(re int i=1;i<=len;++i) { int to=str[i]-'a';//换算成在Trie树上的节点的编号 if(!trie[id][to]) trie[id][to]=++tot;//如果没有那个节点,就新建 id=trie[id][to];//转移到下一个节点 } end[id]=1;//标记字符串的结束节点 } il bool search(char *str) {//检索str字符串在Trie树中是否出现过 int id=1,len=strlen(opt+1); for(re int i=1;i<=len;++i) { int to=str[i]-'a'; id=trie[id][to]; if(!id) return 0;//如果有一个字符串没有,那肯定没有 } return end[id];//全部遍历完后,返回该节点是否是结束节点 //因为存在str只是其中一个字符串的前缀的情况,不能直接返回1 } ``` 讲完了$Trie$,我就直接扔几道练手题: 1.[P2580 于是他错误的点名开始了(类似模板题)](https://www.luogu.com.cn/problem/P2580)[(Trie树题解)](https://www.luogu.com.cn/blog/henry-y/xiang-jie-Trie)[(我的Trie树代码)](https://www.luogu.com.cn/record/48065945) 本题新建一个记录结束节点遍历次数的数组为`int`类型(`cnt[i]`),并把记录结束节点的数组改为`int`类型,只要$cnt[i]<=end[i]$就正常,超过就重复了,在$Trie$树中没有就点错了。 [SP4033 PHONELST - Phone List](https://www.luogu.com.cn/problem/SP4033)[(Trie树题解)](https://www.luogu.com.cn/blog/rezerotime/solution-sp4033)[(我的Trie树代码)](https://www.luogu.com.cn/record/48067360) 本题是用$Trie$树求是否出现一个字符串是另一个字符串的前缀,只要在插入操作中顺手判断一下即可(插入过程中有节点是一个字符串的结尾或整个插入过程中不用新建节点就有)。(不过要仔细读题,有输出$NO$,没有输出$YES$) [P2292 [HNOI2004]L语言(AC自动机的题)](https://www.luogu.com.cn/problem/P2292)[(Trie树题解(大佬真的强,用Trie硬过AC自动机))](https://www.luogu.com.cn/blog/jrtz233/solution-p2292)[(我的Trie代码)](https://www.luogu.com.cn/record/48073805) 本题是AC自动机练习题,用普通的$Trie$会$T$最后一个点,但~~面向数据编程~~ 可以倒序插入$Trie$硬过。(**以后还是要老老实实的用AC自动机过一遍**) 思路:设`vis[i]`表示前$1$到$i$可以被表示,倒序插入字符串,从第$i$个下标倒序往前检索,如果在检索过程中找到一个字符串结束标志(设为$j$),就尝试将该字符串拆成$1$到$j-1$和$j$到$i$,看$1$到$j-1$是否能表示,能就令`vis[i]=1`。最后从后往前找到第一个`vis[i]=1`的节点输出即可。 [P2922 [USACO08DEC]Secret Message G](https://www.luogu.com.cn/problem/P2922)[(Trie树题解)](https://www.luogu.com.cn/blog/toyamakasumi/solution-p2922)[(我的Trie树代码)](https://www.luogu.com.cn/record/48074847) 本题求有前$M$个字符串中有多少个和第$M+N$个字符串有相同前缀,可分为两种情况: - 第$M+N$个字符串在$Trie$树上完全匹配(每一个字符在树上都有),直接输出路径上所有$end[i]$之和。(第$M+N$个字符串是别的字符串的前缀) - 第$M+N$个字符串在$Trie$树上第$id$号节点失配,输出路径上所有$end[i]$之和$-end[id]+sum[id]$($sum[id]$表示经过该点的字符串的总数)。(别的字符串是第$M+N$个字符串的前缀,最后要统计经过失配节点的字符串的数量而不只是在失配点结束的字符串的数量) [P4407 [JSOI2009]电子字典](https://www.luogu.com.cn/problem/P4407)[(Trie树题解)](https://www.luogu.com.cn/blog/Hinanawi-Tenshi/solution-p4407)[(我的Trie树代码)](https://www.luogu.com.cn/record/48294137) 本题要在查找函数中修改,我们可以$DFS$查找,对于三种情况(保证没有使用过修改操作): - 删除:如果当前的$DFS$长度$\le$字符串长度,我们可以跳过当前字符,直接找下一个 - 添加:我们枚举$a$到$z$的所有字符,判断其在$Trie$树上是否出现过,出现了就沿着这条边走,且由于是添加,不用加字符串长度 - 替换:我们枚举$a$到$z$的所有字符,判断其在$Trie$树上是否出现过,出现了且该字符不等于我们要找的字符(等于要找的字符就不用花修改次数替换)就沿着这条边走,加$1$字符串长度 最后走到字符串长度$+1$时判断: - 如果这是一个字符串的结尾且没有修改过,那这就是原串 - 如果这是一个字符串的结尾且修改过,看之前是否访问过,没有就标记并加总访问次数 - 否则,无法匹配,直接退出。 [P5335 [THUSC2016]补退选](https://www.luogu.com.cn/problem/P5335)[(题解)](https://www.luogu.com.cn/blog/nofind/p5335-thusc2016-bu-tui-xuan-trie)[(我的代码)](https://www.luogu.com.cn/record/48793920) 思路:定义`siz[]`数组记录$i$节点目前被经过的次数,用$vector$记录$trie$树上每个节点的第一次超过`vector[id].size()`的插入序号,最后按题意输出即可。 # 2.01$Trie$ 学完了$Trie$的常规操作,那我们就来学一点另类的吧! 有一类很恶心的题目,让我们求一串数列中任意两个数的最大异或和,显然,暴力是$O(n^2)$,直接$T$飞了,但学了$Trie$之后,我们就可以将该问题转化为$Trie$树上的问题并加以解决。 什么?一个位运算的题用字符串算法解决?**是的,你没有看错**,咱们就这么干。我们思考一下位运算的本质是什么?将两个数转化为二进制,并对二进制下相同位的$1$或$0$进行操作,那我们直接将这一列数转化为二进制插入$Trie$树中,再$O(n)$遍历每个数,遍历时尽量往相反方向(检索的数这一位是0,就往树上的1的方向走)走,返回该数在数列中的最大异或值,再在所有的值中取$max$即可。(这样还能大大降低$Trie$树空间复杂度大的劣势) 还是放张图来理解: 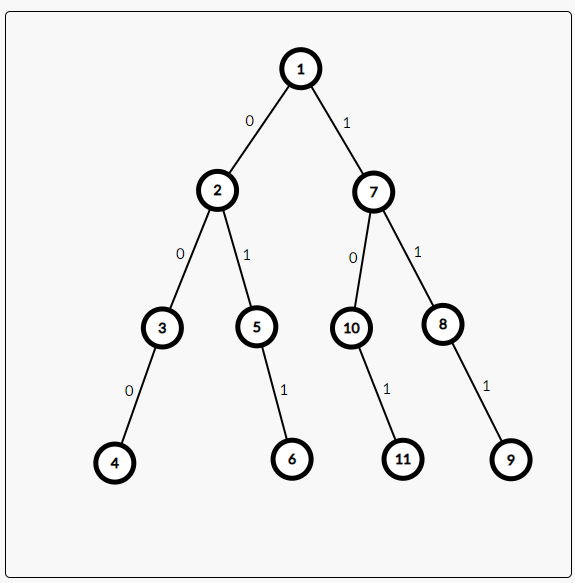 我们向$Trie$树中依次插入$0$(从$1$到$4$的路径)、$3$(从$1$到$6$的路径)、$7$(从$1$到$9$的路径)、$5$(从$1$到$11$的路径). 在遍历$7$时,一直尝试往边权为$0$的节点走,就可以得到$7$的最大异或值$7$,在遍历$3$时,先往边权为$1$的节点走,再尝试往边权为$0$的节点走,走到$10$号节点时因为没有边权为$0$的边,所以不得不往边权为$1$的节点走。得到最大异或值$6$。 代码如下 ```cpp il void insert(int x) {插入该值 int id=1; for(re int i=31;~i;--i) {//i表示2^i bool to=(x>>i)&1;//计算x第i位二进制的值 if(!trie[id][to]) trie[id][to]=++cnt;//常规Trie树操作 id=trie[id][to]; } } il int ask(int x) {//查询最大异或值 int id=1,res=0;//res用于统计最大异或值 for(re int i=31;~i;--i) { bool to=(x>>i)&1; if(trie[id][to^1]) res+=(1<<i),id=trie[id][to^1]; //能往相反方向走,就往相反方向,并更新答案 else id=trie[id][to]; } return res; } ``` 其单次操作的时空复杂度为$O(log$ 值域 $)$,总计$O(nlog$ 值域 $)$,基本可以过很多题了。 [P4551 最长异或路径(板子)](https://www.luogu.com.cn/problem/P4551)[(01Trie题解)](https://www.luogu.com.cn/blog/108510/solution-p4551)[(我的01Trie代码)](https://www.luogu.com.cn/record/48105870) 本题要求树上最长异或路径,我们可以先建一个数组`f[i]`表示节点$i$到根节点(反正是无根树,设为$1$就好了)的路径异或和,再把每一个$f[i]$插入$01Trie$中,检索每个$f[i]$时,尽量往其相反方向走,就可以得到最大异或路径。 [P5283 [十二省联考2019]异或粽子](https://www.luogu.com.cn/problem/P5283)[(用01Trie硬解可持久化Trie的题解)](https://www.luogu.com.cn/blog/qwaszx/solution-p5283)[(我的01Trie代码)](https://www.luogu.com.cn/record/48243407) 本题的标程是可持久化$Trie$,但上面的题解的大佬给了一种神奇的思路:要求前$k$个异或和最大的区间,我们可以先处理前$1$到$i$个数的异或和(设为$sum[i]$),原题就变成在区间$0$到$n$中任取两个下标,使其异或和在前$k$大,我们可以将$sum[i]$在该区间第$rank$大的异或和放入小根堆(堆顶最大)中,每次取出其堆顶,如果$rank$小于$n$,就再在堆中加入$sum[i]$在该区间第$rank+1$大的异或和,那就转化为上一题的板子。 坑点:我们可能会取到$i>j$的情况,但实际上并不存在区间$[i,j]$,所以我们将$k$放大为原来的两倍,最后答案除以$2$即可。 # 3.可持久化$Trie$ 我们使用数据结构时,一般都只维护数据的最新状态,但如果要知道数据集在任意时间内的历史状态,我们怎么办?开$M$(假设修改了$M$次)倍空间把它们都存下来?本身$Trie$就是一个用时间换空间的数据结构,要是真这么做,那直接$MLE$了。 可持久化提供了这样一种思路:每次**只创建数据结构中发生改变的部分的副本**。这样时间复杂度没有增加,空间复杂度仅增长为与时间同级的规模,可以高效的记录一个数据结构的所有历史状态。 那它是怎么运行的? 由可持久化的思路我们可以知道,我们主要对修改操作进行改变(插入一个字符串$s$时): - 1.设当前可持久化$Trie$的根节点为$root$,令$p = root$,$i = 0$ - 2.建立一个新节点$q$,令$root' = q$ - 3. 若$p \neq 0$,则对每种字符$c$,令$trie[q][c]=trie[p][c]$(保证指向原有信息) - 4.建立一个新的节点$q'$,令$trie[q][s_i]=q'$(新建与原有信息不同的指针) - 5.令$p = trie[p][s_i]$,$q=trie[q][s_i]$,$i = i + 1$ - 6.重复步骤$3-5$,直到$i$到达字符串末尾。 光说肯定是理解不了的,我们还是看图吧: 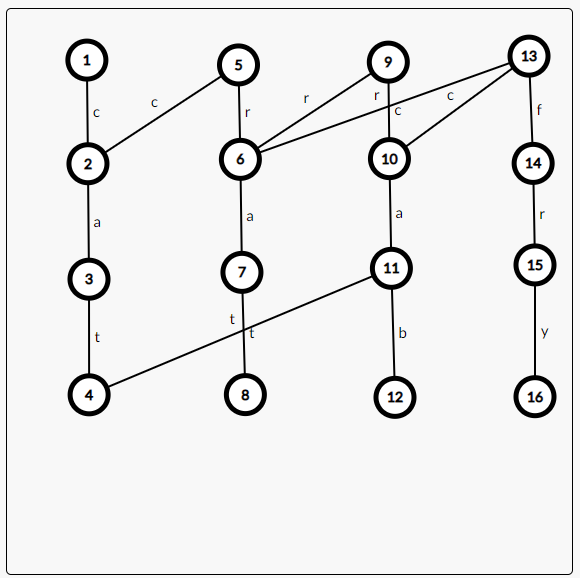 我们向树上依次插入`cat`、`rat`、`cab`、`fry`,那么我们分别从第$1$、$5$、$9$、$13$号节点遍历,就可以得到第$1$、$2$、$3$、$4$次插入后的整颗$Trie$。 代码如下: $01Trie$代码: ```cpp il void insert(int i,int k,int id_pre,int id,int val) { //i表示第几次插入,k表示二进制下该数的第k位 //id_pre表示前一次插入的Trie树的节点 //id表示当前要插入的Trie树的节点 //val是要插入的数字 if(k<0) return ;//插入结束 bool c=(val>>k)&1;//取出val第k为的值 if(id_pre) trie[id][c^1]=trie[id_pre][c^1]; //如果同一层有前一次插入,就复制前一次插入的Trie树 trie[id][c]=++cnt;//新建节点表示本次插入的Trie树 insert(i,k-1,trie[id_pre][c],trie[id][c],val);//进行下一层的插入 } ``` [P4735 最大异或和(可持久化01Trie板子)](https://www.luogu.com.cn/problem/P4735)[(可持久化01Trie题解)](https://m-sea-blog.com/archives/1450)[(我的可持久化01Trie代码)](https://www.luogu.com.cn/record/48116975) [P5283 [十二省联考2019]异或粽子](https://www.luogu.com.cn/problem/P5283)[(可持久化Trie题解)](https://www.luogu.com.cn/blog/tbr-blog/solution-p5283)[(我的可持久化Trie代码)](https://www.luogu.com.cn/record/48258487) 思路:先用$sum[i]$表示前$i$个数的异或和,再参考最大异或和(在序列中$[l,r]$区间内取一个数与给定值异或最大),我们可以维护四元组$(st,l,r,pos)$,表示在区间$[l,r]$中取出一个数$sum[pos]$与$sum[st-1]$的异或和最大,这个数的下标为$pos$,再把该四元组的异或和存入小根堆(堆顶最大)中,每次取出并将其分裂为四元组$(st,l,pos-1,pos')$和$(st,pos+1,r,pos')$即可。 [P4098 [HEOI2013]ALO](https://www.luogu.com.cn/problem/P4098)[(可持久化Trie树题解)](https://www.luogu.com.cn/blog/Youngsc/solution-p4098)[(我的可持久化Trie树代码)](https://www.luogu.com.cn/record/48287373) 思路:枚举每一个数作为区间次大值的区间,求出该数在区间内的异或最大值。 设$l_1$为该数左边第一个比该数大的数的下标,$r_1$为该数右边第一个比该数大的数的下标,$l_2$为该数左边第二个比该数大的数的下标,$r_2$为该数右边第二个比该数大的数的下标。 则该数作为区间次大值的区间为$[l_1+1,r_2-1]$和$[l_2+1,r_1-1]$(其他区间都是这两个区间的子集,就取这两个区间可以使选择最多)。 我们可以运用链表的思想,初始时将$i$的前驱设为$i-1$,$i$的后继设为$i+1$。 - 每一次枚举整个序列的最小值的下标。 - 统计完答案后,就将$i$的前驱的后继连向$i+1$,$i$的后继的前驱连向$i-1$(相当于把该数从链表中删去)。 - 之后每次找序列最小值重复上述操作即可。(可以先$sort$一遍整个序列,在从小到大循环) 因为每一次找的都是序列中的最小值,所以链表中记录的前驱和后继是正确的(最小值的前一下标代表的数和后一下标代表的数肯定比它大),最后转化为区间内取两个数求异或和最大,套可持久化$Trie$数的板子即可。 [P4592 [TJOI2018]异或](https://www.luogu.com.cn/problem/P4592)[(题解)](https://www.luogu.com.cn/blog/Karry5307/solution-p4592)[(给我提供思路的人的代码)](https://www.luogu.com.cn/record/48638593)[(我的代码)](https://www.luogu.com.cn/record/48705345)  如上图所说,本题就是出题人为了加强难度强行将序列上的操作转化到树上,所以我们不得不写树链剖分来迎合出题人。 好了好了,不发牢骚了,本题要我们支持子树内最大异或和和两点间简单路径最大异或和,显然,我们可以先对树进行树剖,按$dfs$序插入每个点的权值。 - 对于求子树内的异或和,我们只需要遍历第$dfn[x]-1 \sim dfn[x]+siz[x]-1$的版本,求出其最大异或和 - 对于求两点简单路径上的最大异或和,我们可以参考树剖的区间修改,对每一条重链分别求出其最大异或和,再在所有的值中取最大值即可。 # 刷题题单 [Trie 树 基础练习 by _Wallace_](https://www.luogu.com.cn/training/5061) # 参考资料 算法竞赛进阶指南 [咸鱼小屋](https://www.luogu.com.cn/blog/sdlang/Trie-study-text)
正在渲染内容...
点赞
3
收藏
0