斐波那契堆详解 - 洛谷保存站

# 斐波那契堆详解+摊还分析(附 带注释C代码)

斐波那契堆是一种可合并堆，支持以下5中操作：

MAKE-HEAP() :  创建和返回一个新的不含任何元素的堆

INSERT(H, x) :    将一个已填入关键字的元素 x 插入堆 H 中

MINIMUM(H) :  返回一个指向堆 H 中具有最小关键字元素的指针

EXTRACT-MIN(H) :  从堆 H 中删除最小关键字的元素， 并返回一个指向该元素的指针

UNION(H1, H2) :  创建并返回一个包含堆 H1 和 H2 所有元素的新堆。 堆 H1 和 堆 H2 由这一操作 “销毁”

除此之外， 斐波那契堆还支持以下两种操作：

DECREASE-KEY(H, x, k) :  将堆 H 中元素 x 的关键字赋予新值 k。 假定新值 k 不大于当前关键字

DELETE(H, x) :  从堆 H 中删除元素 x

## 1. 斐波那契堆结构

一个斐波那契堆是具有最小堆序的有根树的集合。每个有根树都具有最小堆的性质。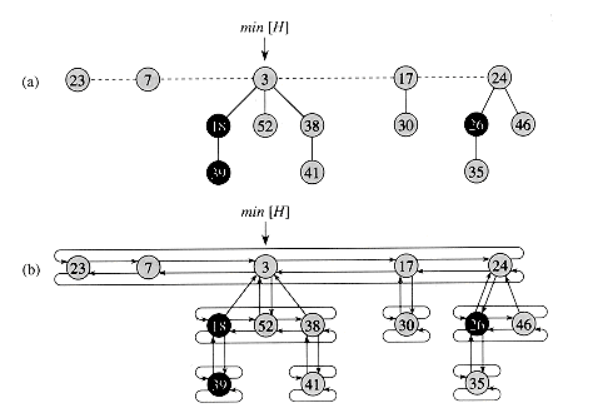

![](https://img2020.cnblogs.com/blog/1328180/202104/1328180-20210405133730092-1952739233.png)

通过 H->min 来访问斐波那契堆 H。 该结点指向具有最小关键字的树的根节点。

在斐波那契堆中， 所有树的根都用其 left 和 right 指针链成一个环形的双链表，该双链表称为斐波那契堆的根链表。

x 的孩子链表也是用环形链表存储的， x->child 指向随机的一个孩子，兄弟间顺序随意。结点度数为孩子数。

```c
typedef struct FibNode *HeapNode;
typedef struct FibNode *Position;
typedef struct FibHeap *FibQueue;

struct FibHeap {
	// 指向堆中最小元素 
	Position min;
	// 堆中的结点个数 
	int NodeNum;
};

struct FibNode {
	// 环形链表，分别指向左右儿子 
	Position LeftSibling;
	Position RightSibling;
	// 指向双亲和其中一个儿子 
	Position Parent;
	Position FirstChild;
	// 结点标记
    bool Mark;
	// 元素值 
	int Element;
	// 结点度数 
	int Degree;
};
```

### 势函数

为了之后的摊还分析， 我们定义斐波那契堆 H 的势函数 
$$
\Phi(H) = t(H) + 2m(H)
$$
$ t(H)$ 表示 H 中根链表中树的数目， $ m(H) $ 表示 H 中已标记的结点数目

### 最大度数

对于摊还分析， 我们先假定， n 个结点的斐波那契堆任何结点度数的上界为 $ D(n)$ , 其中 $D(n) = O(lgn)$

## 2.可合并堆操作

### 创建新堆

```c
// 创建一个新的斐波那契堆 
FibQueue MAKE_HEAP()
{
	FibQueue H = new FibHeap;
	H->min = NULL;
	H->NodeNum = 0;
	return H;
}
```

### 插入一个结点

插入操作很方便， 只需要在根链表中插入一个结点。

如图所示，直接把 21 插入到 3 的左边。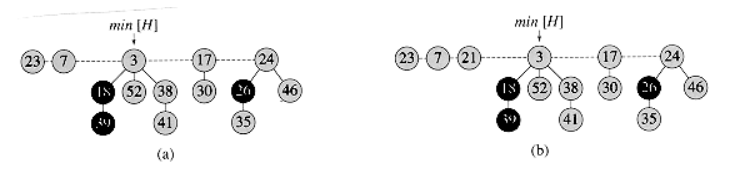

![](https://img2020.cnblogs.com/blog/1328180/202104/1328180-20210405134140015-699181135.png)

```c
// X 插入 H 的 RootList 
void HEAP_INSERT_ROOT(FibQueue H, HeapNode X)
{
	// 更新左兄弟的右指针 
	H->min->LeftSibling->RightSibling = X;
	// X 左兄弟为 H->min 左兄弟 
	X->LeftSibling = H->min->LeftSibling;
	// 更新 H->min 左兄弟 
	H->min->LeftSibling = X;
	// X 右兄弟 H->min
	X->RightSibling = H->min;	
}

// X 插入 Fib H 
void HEAP_INSERT(FibQueue H, HeapNode X)
{
	// 初始化新插入的结点 
	X->Degree = 0;
	X->Parent = NULL;
	X->FirstChild= NULL;
	X->Mark = false;
	// 若堆中没有结点，插入第一个 
	if(H->min == NULL) {
		// 只有 X, 指向自己即可 
		X->LeftSibling = X;
		X->RightSibling = X;
		// 只有X, 所以 H->min = X 
		H->min = X; 
	}
	// 已有结点 
	else {
		// 先把 X 插入循环链表中 (H->min 左边即可)
		HEAP_INSERT_ROOT(H, X);
		// 检查并更新 H->min
		if(X->Element < H->min->Element)
			H->min = X;
	} 
	// 插入一个结点， 结点数 + 1 
	H->NodeNum++; 
}
```

#### 摊还分析

设 $H'$ 是操作后的堆， 则有 $t(H') = t(H) + 1, M(H') = M(H) $, 并且势的增加量为：
$$
((t(H) + 1) + 2m(H)) - (t(H) + 2m(H)) = 1
$$
实际代价为$O(1)$,  所以摊还代价为 $O(1) + 1= O(1) $

### 斐波那契堆合并

```c
// 合并 X 和 Y 的根链表 
void Concatenate(HeapNode X, HeapNode Y)
{
	// 若为空， 不需要合并 
	if(X == NULL || Y == NULL)
		return;
	X->RightSibling->LeftSibling = Y;
	Y->RightSibling->LeftSibling = X;
	X->RightSibling = Y->RightSibling;
	Y->RightSibling = X->RightSibling;
}

// 合并堆 H1, H2 
void HEAP_UNION(FibQueue H1, FibQueue H2)
{
	// 创建一个新堆 
	FibQueue H = MAKE_HEAP();
	// H 指向 H1 
	H->min = H1->min;
	// 把 H2 的 RootList 和 H1 合并
	Concatenate(H->min, H2->min);
    return H;
} 
```

### 抽取最小结点

首先把最小结点 X 的儿子都上提到根链表中，之后把 X 从链表中移除。

先把 H->min 随意指向一个根节点， 之后的 CONSOLIDATE 和合并根结点并找到 H->min。

![](https://img2020.cnblogs.com/blog/1328180/202104/1328180-20210405134415965-294582787.png)

```c
// X 从 H RootList 移除 
void HEAP_REMOVE_ROOT(HeapNode X)
{
	// X 的左儿子指向右儿子 
	X->LeftSibling->RightSibling = X->RightSibling;
	// X 的右儿子指向左儿子 
	X->RightSibling->LeftSibling = X->LeftSibling; 
}

HeapNode HEAP_EXTRACT_MIN(FibQueue H)
{
	// 首先把 Z 的所有儿子上移到 H 的 RootList 中 
	HeapNode Z = H->min;
	HeapNode X, Y;
	if(Z != NULL) {
		X = Z->FirstChild;
		// 遍历 Z 的儿子 
		while(Z->Degree--) {
			// X 插入后右兄弟改变， 提前记录 
			Y = X->RightSibling;
			// 插入 RootList 
			HEAP_INSERT_ROOT(H, X);
		//	PrintRoot(H);
			// 更新双亲 
			X->Parent = NULL;
			// 下一个兄弟
			X = Y; 
		}
		// 将 Z 从 RootList 移除
		HEAP_REMOVE_ROOT(Z);
		// Z 指向自己， 说明移除后堆为空 
		if(Z == Z->RightSibling)
			H->min = NULL; 
		else {
			// 先把 H->min 随意指向一个结点 
			H->min = Z->RightSibling;
		//	PrintRoot(H); 
			// 调整堆结构
			HEAP_CONSOLIDATE(H);
		}
		// 移除结点， 结点数 - 1 
		H->NodeNum--;
	}
	return Z; 
}
```

#### 合并根链表

这是斐波那契堆最关键的一步，通过合并使时间复杂度降低。

合并根链表的过程为重复执行以下步骤，知道根链表中每一个根都有不同度数。

1. 在根链表中找到两个具有相同度数的根 x 和 y, 不失一般性，假定 $ x.key\leq y.key$
2. 把 y 链接到 x: 根链表中移除 y, 调用 HEAP-LINK, 使 y 成为 x 的孩子。 x.degree + 1， 清除 y 的标记(y 的作用之后会讲到)

使用辅助数组么 A[0, ... D(n)]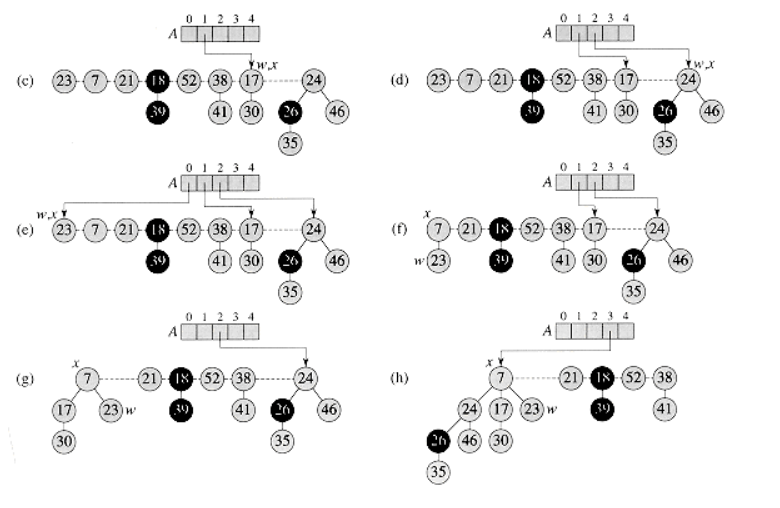

![](https://img2020.cnblogs.com/blog/1328180/202104/1328180-20210405134443158-1050606330.png)

```c
// 把 Y 合并成 X 的儿子 
void MAKECHILD(HeapNode X, HeapNode Y)
{
	X->Degree++;
	// 找到 X 的第一个儿子, 把 Y 插入到第一个儿子左边 
	HeapNode Z = X->FirstChild;
	// X 没有儿子 
	if(Z == NULL) {
		Y->LeftSibling = Y;
		Y->RightSibling = Y;
		X->FirstChild = Y;
	} 
	// 已经有儿子 
	else {
		// 更新左兄弟的右兄弟 
		Z->LeftSibling->RightSibling = Y;
		// 更新 Y 的左兄弟 
		Y->LeftSibling = Z->LeftSibling; 
		// 更新 Z 的左兄弟 
		Z->LeftSibling = Y;
		// 更新 Y 的右兄弟 
		Y->RightSibling = Z;
	}
	// 更新 Y 的双亲 
	Y->Parent = X; 
}

void HEAP_LINK(FibQueue H, HeapNode X, HeapNode Y)
{
	// 把 Y 从 RootList 移除
	// Y 作为 X 的儿子， X 度数 + 1
	MAKECHILD(X, Y);
	Y->Mark = false;	
}

// 调整后的 FibHeap 满足 RootList 中没有相同度数的根 
void HEAP_CONSOLIDATE(FibQueue H)
{
	// 辅助数组 A[i] 指向一个 degree 为 i 的根 
	// Degree 的上界为 log n 
	int num = (log(H->NodeNum) + 1) * 2;

for(int i = 0; i < num; i++)
		A[i] = NULL;
	HeapNode M = H->min;
	HeapNode R = M->RightSibling;
	HeapNode X, Z;
	// 遍历 RootList
	do {
		X = R;
		Z = X;
		R = X->RightSibling;
		int d = X->Degree;
		// 存在 degree 相同的结点 
		while(A[d] != NULL) {
			HeapNode Y = A[d];
			// X 为小结点， 合并在堆顶 
			if(X->Element > Y->Element)
				NodeSwap(&X, &Y);
			// 合并 X, Y 
			HEAP_LINK(H, X, Y);
			// 合并后的度数为 d + 1 
			A[d] = NULL;
			d++;
		}
		// 循环结束， A[d] = X 
		A[d] = X;
		//PrintRoot(H);
	} while(Z != M);
	
	H->min = NULL;
	
	// 把 A[i] 重新放入 RootList 中 
	for(int i = 0; i < num; i++) {
		HeapNode X = A[i];
		// A[i] 存在， 插入 RootList 
		if(X != NULL)
			// 插入空 RootList 
			if(H->min == NULL) {
				// 只有 X, 指向自己即可 
				X->LeftSibling = X;
				X->RightSibling = X;
				// 只有X, 所以 H->min = X 
				H->min = X; 
			} 
			// 已有结点 
			else {
				// 先把 X 插入循环链表中 (H->min 左边即可)
				HEAP_INSERT_ROOT(H, X);
				// 检查并更新 H->min
				if(X->Element < H->min->Element)
					H->min = X;
			}
	}
}
```

#### 摊还分析

在 CONSOLIDATE 中， 根链表的大小最大为 $ D(n) + t(H) - 1$。 其中 for 循环遍历了根链表， 而 while循环的合并操作最多会合并根结点个数次 (每次合并结点个数 - 1) ，因此抽取最小结点的实际工作量为 $O(D(n) + t(H)) $

抽取前的势为 $t(H) + 2m(H)$ , 因为最多有 D(n) + 1 个结点留下且没有任何结点被标记,所以操作后最大的势为 $D(n) + 1+2m(H)$

摊还代价最多为：
$$
\begin{aligned}&O(D(n) + t(H)) +((D(n) + 1)+2m(H)) - (t(H)+2m(H))\\
=&O(D(n)) + O(t(H)) - t(H)\\
=&O(D(n))
\end{aligned}
$$

## 3.关键字减值与删除

### 关键字减值

找到 X 后， 把 X 和父亲 Y 断开， 并把 X 加入到根链表中。

这里的关键在于级联操作， X 断开后， Y 的标记可能改变，导致 Y 也要继续断开， 以维护斐波那契堆。

```c
// 切断 Y 和 X 
void CUT(FibQueue H, HeapNode X, HeapNode Y)
{
	// 把 X 从 Y 的儿子列表中移除， Y.degree - 1
	HEAP_REMOVE_CHILD(X, Y);
	// 把 X 加入到 RootList 中 
	HEAP_INSERT_ROOT(H, X);
	// X 为根 
	X->Parent = NULL;
	X->Mark = false; 
}

void HEAP_DECREASE_KEY(FibQueue H, HeapNode X, int k) 
{
	// 值只能减小， 不能增大 
	if(k > X->Element) {
		printf("new key is greater than current key\n");
		return;
	}	
	X->Element = k;
	HeapNode Y = X->Parent;
	// 如果 Y 存在并且 X 需要上移
	if(Y != NULL && X->Element < Y->Element) {
		CUT(H, X, Y);
		CASCADING_CUT(H, Y);
	}
	// 更新 H->min
	if(X->Element < H->min->Element)
		H->min = X; 
} 
```

#### mark 标记

使用 mark 属性记录结点的状态。假定下面的步骤已经发正在了 X 上

1.  在某个时刻， X 是根。
2.  然后 X 被链接到另一个结点(成为孩子结点)
3.  然后 X 有两个孩子被切断操作切除。

一旦失掉第二个孩子， 就切断 X 与父结点的链接，使成为新的根。这就是CASCADING(级联)的意义所在。

因此每当 X 被移至根上时， mark 为 false , 回到状态一。

```c
/* 判断 Y 是否要和父亲切断
   1. Y 曾经作为根
   2. Y 之后成为了孩子结点(因为 Z 是 Y 的父亲)
   3. 然后 Y 的两个孩子被切除了 (切除第一个孩子 Mark 为 True, 切除第二个孩子 Y 和 Z 分离)
*/ 
void CASCADING_CUT(FibQueue H, HeapNode Y)
{
	HeapNode Z = Y->Parent;
	if(Z != NULL)
		// 切断了一个儿子， 标记为 true, 为下次切断做准备 
		if(Y->Mark == false)
			Y->Mark = true;
		// 符合切断条件， 递归向上继续切断 
		else {
			//  
			CUT(H, Y, Z);
			CASCADING_CUT(H, Z); 
		}
}
```

#### 摊还分析

假定一次 DECREASE-KEY 调用了 c 次 CASCADING, 则实际代价为 $ O(c)$

接下来计算势的变化。除了最后一次级联， 其余每次都会使一个结点的标记变为 false, 因此最多有 $ m(H)  + c - 2$ 个被标记的结点(减少了 $c - 1$ 个， 最后一次可能会增加一个， cut 的结点可能为 false) 。 此时的斐波那契堆包含  $ t(H) + c $ 棵树。

所以势的变化最多为
$$
((t(H) + c) + 2(m(H) - c + 2)) - (t(H) + 2m(H)) = 4 - c
$$
所以斐波那契堆的摊还代价至多是
$$
O(c) + 4 - c = O(1)
$$

### 删除结点

```c
// 删除堆中结点 X 
void HEAP_DELETE(FibQueue H, HeapNode X)
{
	HEAP_DECREASE_KEY(H, X, -INFINITY);
	HEAP_EXTRACT_MIN(H);
}
```

代价为 DECREASE-KEY 和 EXTRACT-MIN 时间之和， 所以 DELETE摊还时间为 $ O(lg n)$

## 4.最大度数的界

我们之前还遗留了一个最重要的证明， 即任意结点的度数的上界 $D(n) 为 O(lgn)$

特别地， 要证明 $D(n) <= \lfloor\log_{\phi}^{n}\rfloor$, 这里 $\phi$ 是黄金分割率，
$$
\phi = (1+\sqrt5) /2=1.61803...
$$
关键在于定义 size(x) 为以 X 为根的子树中包括 X 本身的结点个数。 证明 size(x) 是 x.degree 的幂。

##### 引理 1

$设\  x \ 是斐波那契堆任意结点， 并假定\ x.degree \ge k。 设\ y_1, y_2, \cdots y_k 表示\ x\ 的孩子， 并以链入的先后顺序排序，\\ 则\ y_1.degree\ge0, 且对于\ i= 1, 2, 3, \cdots, k, 有\ y_i.degree \ge i - 2。$

##### 证明

显然, $y_1.degree \ge 0$， 对于 $i\ge 2$， 注意到 $y_i$ 一定在 $y_1, y2, \cdots y_{i- 1}$ 后键入，因此有 $x.degree \ge i - 1$。 而结点 $y$ 成为 X  儿子的条件是 $x.degree = y_i.degree$，  所以此时一定有 $y_i \ge i - 1$,  之后结点 $y$ 最多失去一个孩子(失去两个孩子被切除)。综上，$y_i.degree\ge i - 2$

##### 引理 2

对于斐波那契数列:

有另一种表示方法
$$
F_{k+2} = 1 + \sum_{i=0}^{k}F_i
$$

##### 证明

做归纳假设 $F_{k+1}=1+\sum_{i=0}^{k-1}F_{i}$
$$
F_{k+2}=F_k+F_{k+1}=F_k+(1+\sum_{i=0}^{k-1}F_i)=1+\sum_{i=0}^{k}F_i
$$

##### 引理 3

对于所有整数 $k\geq0$， 斐波那契的第 $k+2$ 个数满足 $F_{k+2}\ge\phi^{k}$

##### 证明

假定对于 $i = 0, 1, \cdots, k-1, 有\ F_{i+2}>\phi^{i}$

于是
$$
\begin{aligned}
F_{k+2}&=F_{k+1}+F_k\\
&\geq\phi^{k+1} + \phi^{k-2}\\
&=\phi^{k-2}(\phi+1)\\
&=\phi^{k-2} \cdot\phi^2\\
&=\phi^k
\end{aligned}
$$

#####  引理 4

设 x 是斐波那契堆中的任意结点, 并设 k = x.degree， 则有 $size(x)\ge F_{k+2}\ge \phi^k，$

##### 证明

显然， $s_0 = 1, s_1 = 2。 s_k$ 最大为 $size(x)$ , $s_k$ 的值递增。
$$
size(x)\ge s_k \ge 2+\sum_{i=2}^ks_{y_i.degree}\ge 2+\sum_{i = 2}^ks_{i-2}
$$
利用 $s_k\ge F_{k+2}$ 归纳
$$
\begin{aligned}
s_k&\ge 2+\sum_{i=2}^ks_{i-2}\ge2+\sum _{i = 2}^kF_i=1+\sum_{i=0}^k F_i\\
&= F_{k+2}\\
&\ge \phi^k
\end{aligned}
$$

##### 推论

一个 n 个结点的斐波那契堆中任意结点的最大度数 D(n) 为 O(lgn)

##### 证明

$n\ge size(x)\ge\phi^k$ , 取对数， $k \le \log_{\phi}^n$,  所以任意结点的最大度数 D(n) 为 O(lgn)

## 5. 完整代码

```c
#include <iostream>
#include <cmath>

using namespace std;

typedef struct FibNode *HeapNode;
typedef struct FibNode *Position;
typedef struct FibHeap *FibQueue;

struct FibHeap {
	// 指向堆中最小元素 
	Position min;
	// 堆中的结点个数 
	int NodeNum;
};

struct FibNode {
	// 环形链表，分别指向左右儿子 
	Position LeftSibling;
	Position RightSibling;
	// 指向双亲和其中一个儿子 
	Position Parent;
	Position FirstChild;
	bool Mark;
	// 元素值 
	int Element;
	// 结点度数 
	int Degree;
};

HeapNode *A;

void PrintNode(HeapNode X)
{
	cout<<X->Element<<endl;
	cout<<X->LeftSibling->Element<<" "<<X->RightSibling->Element<<endl;
	cout<<endl;
}

void PrintRoot(FibQueue H)
{
	//cout<<"The RootList is:"<<endl;
	HeapNode M = H->min;
	HeapNode X = M;
	do {
		X = X->RightSibling;
		PrintNode(X);
	} while(X != M);
}

// 创建一个新的斐波那契堆 
FibQueue MAKE_HEAP()
{
	FibQueue H = new FibHeap;
	H->min = NULL;
	H->NodeNum = 0;
	return H;
}

// X 插入 H 的 RootList 
void HEAP_INSERT_ROOT(FibQueue H, HeapNode X)
{
	// 更新左兄弟的右指针 
	H->min->LeftSibling->RightSibling = X;
	// X 左兄弟为 H->min 左兄弟 
	X->LeftSibling = H->min->LeftSibling;
	// 更新 H->min 左兄弟 
	H->min->LeftSibling = X;
	// X 右兄弟 H->min
	X->RightSibling = H->min;	
}

// X 从 H RootList 移除 
void HEAP_REMOVE_ROOT(HeapNode X)
{
	// X 的左儿子指向右儿子 
	X->LeftSibling->RightSibling = X->RightSibling;
	// X 的右儿子指向左儿子 
	X->RightSibling->LeftSibling = X->LeftSibling; 
}

// 把 X 从 Y 的儿子列表中移除
void HEAP_REMOVE_CHILD(HeapNode X, HeapNode Y)
{
	Y->Degree--;
	// 防止 Y 的 Child 连到 X 的情况 
	Y->FirstChild = X->RightSibling; 
	// 把 X 从链表中移除 
	HEAP_REMOVE_ROOT(X);
	// Y 没有儿子了 
	if(!Y->Degree)
		Y->FirstChild = NULL;
}

// 交换 X, Y 
void NodeSwap(HeapNode *X, HeapNode *Y) 
{
	HeapNode Temp;
	Temp = *X;
	*X = *Y;
	*Y = Temp; 
}

// 把 Y 合并成 X 的儿子 
void MAKECHILD(HeapNode X, HeapNode Y)
{
	X->Degree++;
	// 找到 X 的第一个儿子, 把 Y 插入到第一个儿子左边 
	HeapNode Z = X->FirstChild;
	// X 没有儿子 
	if(Z == NULL) {
		Y->LeftSibling = Y;
		Y->RightSibling = Y;
		X->FirstChild = Y;
	} 
	// 已经有儿子 
	else {
		// 更新左兄弟的右兄弟 
		Z->LeftSibling->RightSibling = Y;
		// 更新 Y 的左兄弟 
		Y->LeftSibling = Z->LeftSibling; 
		// 更新 Z 的左兄弟 
		Z->LeftSibling = Y;
		// 更新 Y 的右兄弟 
		Y->RightSibling = Z;
	}
	// 更新 Y 的双亲 
	Y->Parent = X; 
}

void TEST(HeapNode X, HeapNode Y)
{
	X->LeftSibling = Y;
}

void HEAP_LINK(FibQueue H, HeapNode X, HeapNode Y)
{
	// 把 Y 从 RootList 移除
	// Y 作为 X 的儿子， X 度数 + 1
	MAKECHILD(X, Y);
	Y->Mark = false;	
}

// 切断 Y 和 X 
void CUT(FibQueue H, HeapNode X, HeapNode Y)
{
	// 把 X 从 Y 的儿子列表中移除， Y.degree - 1
	HEAP_REMOVE_CHILD(X, Y);
	// 把 X 加入到 RootList 中 
	HEAP_INSERT_ROOT(H, X);
	// X 为根 
	X->Parent = NULL;
	X->Mark = false; 
}

/* 判断 Y 是否要和父亲切断
   1. Y 曾经作为根
   2. Y 之后成为了孩子结点(因为 Z 是 Y 的父亲)
   3. Y 的两个孩子被切除了 (切除第一个孩子 Mark 为 True, 切除第二个孩子 Y 和 Z 分离)
*/ 
void CASCADING_CUT(FibQueue H, HeapNode Y)
{
	HeapNode Z = Y->Parent;
	if(Z != NULL)
		// 切断了一个儿子， 标记为 true, 为下次切断做准备 
		if(Y->Mark == false)
			Y->Mark = true;
		// 符合切断条件， 递归向上继续切断 
		else {
			//  
			CUT(H, Y, Z);
			CASCADING_CUT(H, Z); 
		}
}

// 合并 X 和 Y 的根链表 
void Concatenate(HeapNode X, HeapNode Y)
{
	// 若为空， 不需要合并 
	if(X == NULL || Y == NULL)
		return;
	X->RightSibling->LeftSibling = Y;
	Y->RightSibling->LeftSibling = X;
	X->RightSibling = Y->RightSibling;
	Y->RightSibling = X->RightSibling;
}

// 删除堆中结点 X 
void HEAP_DELETE(FibQueue H, HeapNode X)
{
	HEAP_DECREASE_KEY(H, X, -INFINITY);
	HEAP_EXTRACT_MIN(H);
}
```

附博客地址
https://www.cnblogs.com/wuenze/p/14618312.html

正在渲染内容...