线段树学习笔记 最后更新于 2025-05-01 23:59:02

看一道题目吧~~ ## P3374 # 【模板】树状数组 1 ## 题目描述 如题，已知一个数列，你需要进行下面两种操作： - 将某一个数加上 $x$ - 求出某区间每一个数的和 ## 输入格式 第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。 第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。 接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下： - `1 x k` 含义：将第 $x$ 个数加上 $k$ - `2 x y` 含义：输出区间 $[x,y]$ 内每个数的和 ## 输出格式 输出包含若干行整数，即为所有操作 $2$ 的结果。 ## 样例 #1 ### 样例输入 #1 ``` 5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4 ``` ### 样例输出 #1 ``` 14 16 ``` ## 提示 【数据范围】 对于 $30\%$ 的数据，$1 \le n \le 8$，$1\le m \le 10$； 对于 $70\%$ 的数据，$1\le n,m \le 10^4$； 对于 $100\%$ 的数据，$1\le n,m \le 5\times 10^5$。 样例说明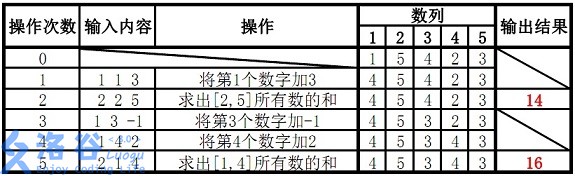：  故输出结果14、16 ---------- 读完本题，我们考虑用线段树来做 线段树，顾名思义，就是用线段组成的树，这里我们的每一个结点表示的是一段区间的和。 其实线段树就像一个二叉树，我们考虑如何建树： 首先根节点肯定代表的是1~$n$所有的和，左儿子代表的是1~$n/2$的值的和。右儿子代表的是$n/2+1$~$n$的所有值的和，以此类推，所以这样我们就可以得到一个线段树。 然后我们再来看单点修改的操作，其实很简单，假设要将点$x$的值加上$k$,我们就从根节点递归下去，把有包含$x$值的线段加上$k$ 最后看查询，首先看在左子树还是在右子树，如果刚好能找到区间，就可以输出，如果左右两边都有，就把左右两边的都加起来。 代码很难看~~ ```c++ #include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 5e5 + 10; int a[N],f[N*4]; inline void buildtree(int k,int l,int r) { if(l == r) { f[k] = a[l]; return; } int mid = (l + r) >> 1; buildtree(k + k,l, mid); buildtree(k + k + 1,mid + 1, r); f[k] = f[k + k] + f[k + k + 1]; } inline void add(int k,int l,int r,int x,int y) { f[k] += y; if(l == r) return; int mid = (l + r) >> 1; if(x <= mid) add(k + k, l, mid, x, y); else add(k + k + 1, mid + 1, r, x, y); } int calc(int k,int l,int r,int s, int e) { if(l == s && r == e) return f[k]; int mid = (l + r) >> 1; if(e <= mid) return calc(k + k, l, mid, s, e); else { if(s > mid) return calc(k + k + 1, mid + 1, r, s, e); else return calc(k + k, l, mid, s, mid) + calc(k + k + 1, mid + 1, r, mid + 1, e); } } int main() { int n,m; cin >> n >> m; for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); buildtree(1,1,n); for (int i = 1; i <= m; i ++ ) { int opt,x,y; scanf("%d%d%d", &opt, &x, &y); if(opt == 1) add(1,1,n,x,y); else cout << calc(1,1,n,x,y) << endl; } return 0; } 求点赞！！