题解：「WWOI R1」WsW 的田地

前言

数据卡掉了出题人和验题人写出的所有错解，并且全输出 Angry 不得分。

思路

题意实际上是，给定两个矩阵，每次对矩阵进行一些操作，问每次操作后两个矩阵是否相等。两个矩阵相等，等价于两个矩阵对应位置相减均为 $0$，这样就将两个矩阵上的操作转化为了一个矩阵上的操作。

想判断一个矩阵是否每个点均为 $0$ 太困难了，我们希望能找到一个更简洁的方法来描述这个矩阵，最好可以只使用一个整数。
哈希算法就是用于将一个复杂的、不好描述的信息，映射为一个简洁的、容易描述的信息。

接下来使用随机赋权哈希解决这个问题。

我们将相减后矩阵上每个点减出来的数字成为这个点上的数值。
一个很简单的想法是，我们可以将所有数值加起来作为这个矩阵的哈希值，当哈希值为 $0$ 时我们认为矩阵每个位置上的数值均为 $0$。但实际上这样有较大的可能出错，因为每个点对哈希值的影响都是一样的。
如何让每个点对哈希值的影响不同呢？可以对矩阵的每个点随机赋权，将所有点上数值乘以权值的积加起来，作为哈希值。
当哈希值为 $0$ 时，这个矩阵大概率每个点上的数值均为 $0$。每个点上的数值均为 $0$ 时，哈希值必定为 $0$。

我们可以把哈希值为 $0$ 这个必要，但小概率不充分的条件，看做矩阵上每个点的数值均为 $0$ 的充要条件。

接下来考虑如何求出药水作用区间点的权值之和。
对于药水 $1$，作用区间是个十字，只需要预处理每行、每列的权值和即可。
对于药水 $2$，作用区间是个矩形，只需要用二维前缀和计算即可。
对于药水 $3$，作用区间是个平行四边形，可以将第 $i$ 行向左平移 $i$ 个单位，发现作用区间就变成了矩形。只需要在平移后的矩阵上用二维前缀和计算即可。下图中用红色表示药水 $3$ 的作用区间，以及其平移后的样子。

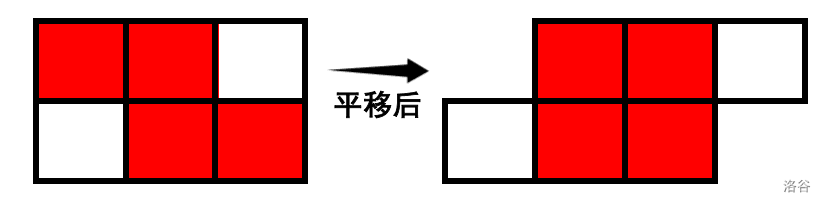
时间复杂度为 $O(nm+q)$。

代码

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
int n,m,q;
ull p[805][805];
ull sum[2][805][1605];
ull now;
mt19937_64 rng(time(0));

ull getsum(int xx,int yy,int x,int y,bool f){
	xx=min(n,xx); x=min(n,x);
	yy=min(m+n,yy); y=min(m+n,y);
	return sum[f][xx][yy]+sum[f][x-1][y-1]-sum[f][xx][y-1]-sum[f][x-1][yy];
}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			p[i][j]=rng();
			int x; cin>>x;
			now+=x*p[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int x; cin>>x;
			now-=x*p[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m+n;j++){
			sum[0][i][j]=p[i][j]+sum[0][i-1][j]+sum[0][i][j-1]-sum[0][i-1][j-1];
			sum[1][i][j-i+n]=p[i][j]+sum[1][i-1][j-i+n]+sum[1][i][j-i+n-1]-sum[1][i-1][j-i+n-1];
		}
	}
	cin>>q;
	while(q--){
		int t,f,x0,y0,k;
		cin>>t>>f>>x0>>y0>>k;
		f=(f?-1:1);
		if(t==1)now+=(getsum(x0,m,x0,1,0)+getsum(n,y0,1,y0,0)-p[x0][y0])*f*k;
		if(t==2){
			int u,v;cin>>u>>v;
			now+=getsum(x0+u,y0+v,x0,y0,0)*f*k;
		}
		if(t==3){
			int u,v;cin>>u>>v;
			now+=getsum(x0+u,y0+v+n-x0,x0,y0+n-x0,1)*f*k;
		}
		if(now)cout<<"Angry";
		else cout<<"Happy";
		if(q)cout<<'\n';
	}
	return 0;
}