主页
搜索
最近更新
数据统计
申请密钥
系统公告
1
/
1
请查看完所有公告
斜率优化(二)
最后更新于 2025-07-31 06:08:01
作者
bladrrxy
分类
算法·理论
复制 Markdown
查看原文
删除文章
更新内容
前置知识:[斜率优化(一)](https://www.luogu.com.cn/blog/bladrrxy/xie-lv-you-hua-yi-post), [CDQ分治](https://www.luogu.com.cn/blog/bladrrxy/cdq-fen-zhi) 斜率优化(一)中的斜率优化要求状态转移方程形如 $dp_i = \min/\max{y(j) - k(i) \times x(j)}$,并且 $x(j)$ 必须单调。 如果 $x(j)$ 不单调呢?试着让它单调。 用CDQ分治,先递归处理左半部分并把它按横坐标排序,用左半部分建凸壳来更新右半部分,再递归处理右半部分。 时间复杂度 $O(n \log ^ 2 n)$。 注意到,这个排序可以在分治时归并,时间复杂度再次优化至 $O(n \log n)$。 $y(j)$ 的取值一般与 $dp_j$ 有关,可以在递归基($l == r$)时更新 $y_l$。 看一道题:[[SDOI2012] 基站建设](https://www.luogu.com.cn/problem/P2497) 设 $dp_i$ 表示让第 $i$ 个基站接收到信号的最小代价,则 $$dp_i = dp_j + \sqrt{r'_i} + v_i$$ 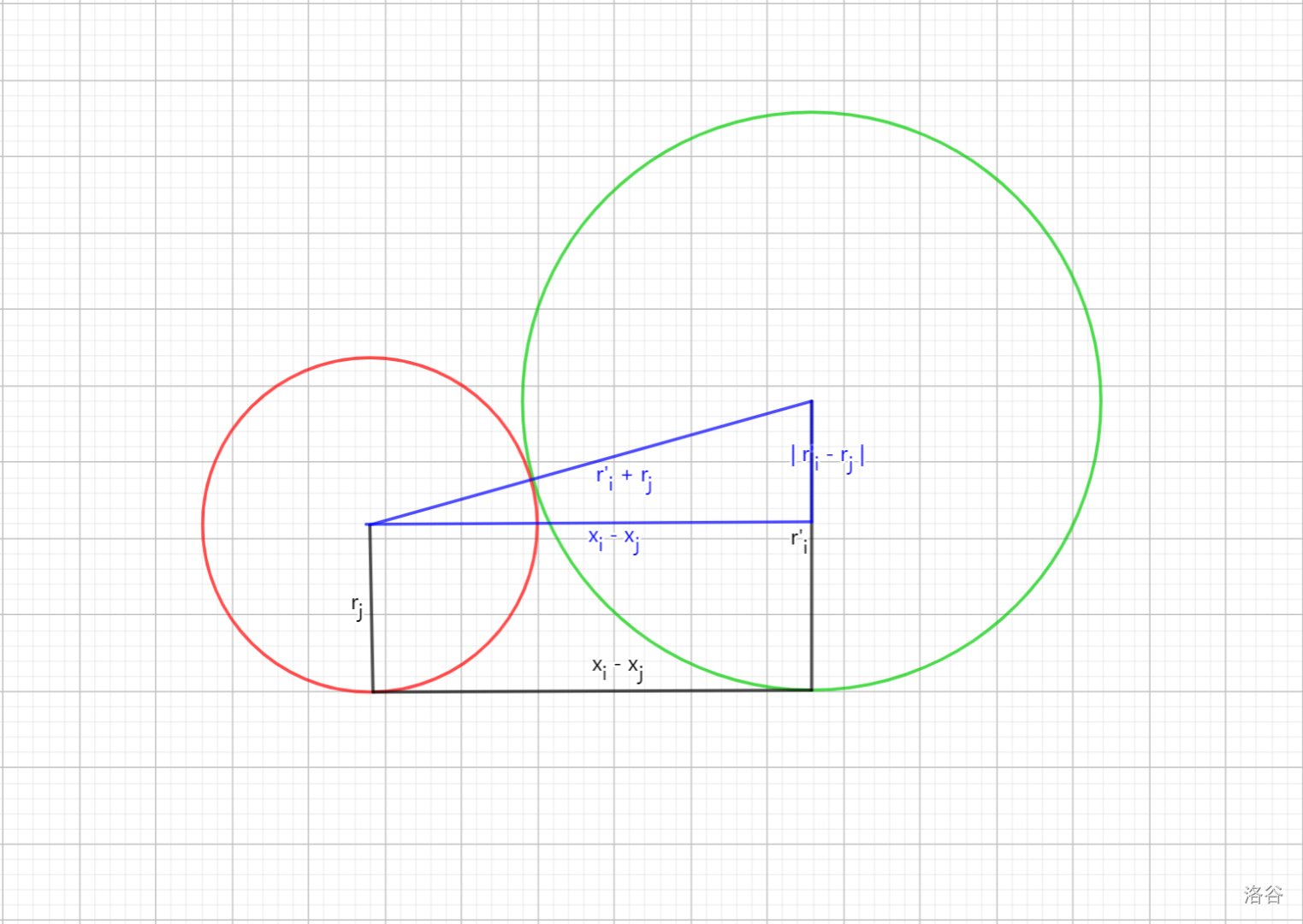 由上图可知, $$ \begin{aligned} (x_i - x_j) ^ 2 + (r'_i - r_j) ^ 2 &= (r'_i + r_j) ^ 2\\ (x_i - x_j) ^ 2 &= 4 r'_i r_j\\ r'_i &= \displaystyle{\frac{(x_i - x_j) ^ 2}{4 r_j}}\\ \sqrt{r'_i} &= \displaystyle{\frac{x_i - x_j}{2 \sqrt{r_j}}} \end{aligned} $$ 所以, $$dp_i = dp_j + \displaystyle{\frac{x_i - x_j}{2 \sqrt{r_j}}} + v_i$$ 设 $t_j = \displaystyle{\frac{1}{2 \sqrt{r_j}}}$,原式变为 $$ \begin{aligned} dp_i &= dp_j + t_j (x_i - x_j) + v_i\\ dp_i &= dp_j + t_j x_i - t_j x_j + v_i\\ dp_i - v_i &= dp_j - x_j t_j + x_i t_j \end{aligned} $$ 开始斜率优化。 设 $x(j) = -t_j$,$y(j) = dp_j - x_j t_j$,$k(i) = x_i$。 但是 $x(j)$ 不单调,用CDQ分治。 代码: ```cpp #include<bits/stdc++.h> using namespace std; using ll = long long; using ld = long double; constexpr int N{500005}; struct node { ll x, r, v; ld t; } a[N]; struct point { ld x, y; } b[N], tmp[N]; int n, s[N], top; ll m; ld dp[N]; void Min(ld& x, ld y) { x > y && (x = y); } void cdq(int l, int r) { //递归基 if(l == r) { b[l] = point{a[l].t, dp[l] - a[l].x * a[l].t}; return; } int mid = (l + r) >> 1; //递归处理左半部分 cdq(l, mid); //用左半部分建凸壳(单调栈) top = 0; for(int i = l; i <= mid; ++i) { while(top > 1 && (b[s[top]].y - b[s[top - 1]].y) * (b[i].x - b[s[top]].x) >= (b[i].y - b[s[top]].y) * (b[s[top]].x - b[s[top - 1]].x)) --top; s[++top] = i; } //更新右半部分 for(int i = mid + 1; i <= r; ++i) { while(top > 1 && b[s[top]].y - b[s[top - 1]].y >= -a[i].x * (b[s[top]].x - b[s[top - 1]].x)) --top; Min(dp[i], a[i].v + b[s[top]].y + a[i].x * b[s[top]].x); } //递归处理右半部分 cdq(mid + 1, r); //归并排序 int i{l}, j{mid + 1}, t{l}; while(i <= mid && j <= r) { if(b[i].x <= b[j].x) tmp[t++] = b[i++]; else tmp[t++] = b[j++]; } while(i <= mid) { tmp[t++] = b[i++]; } while(j <= r) { tmp[t++] = b[j++]; } copy(tmp + l, tmp + r + 1, b + l); } int main() { cin >> n >> m; for(int i = 1; i <= n; ++i) { cin >> a[i].x >> a[i].r >> a[i].v; a[i].t = 1 / sqrt(a[i].r) / 2; dp[i] = 5e12; } dp[1] = a[1].v; cdq(1, n); ld ans{5e12}; for(int i = 1; i <= n; ++i) { if(a[i].x + a[i].r >= m) Min(ans, dp[i]); } cout << fixed << setprecision(3) << ans << endl; return 0; } ```
正在渲染内容...
点赞
0
收藏
0