五一算法集训

# 五一算法集训：
## Day 1：
网这么卡，鼠标滚轮不好用，气 S 了。
#### -- 上午 --
### 数据结构：
**数据结构全一册：从入门到入坟。**

最基本的数据结构就是变量，因为数据结构就是用来存变量的。再高一阶就是数组，能存很多东西。再高一点就是由数组进化而来的队列和栈。还是，栈先进后出，队列先进先出（FIFO）。

### 队列&栈&单调队列：

**队列**挺简单，~~但是这个颓物不会单调队列~~。声明一个队列只需要先写个 `#include<queue>` 再写个 `queue<队列元素类型> 变量名;` 就行。

一些函数：`q.push(x);` 向队尾加入元素；`q.pop();` 删除队头；`q.front();` 获取队头元素；`q.size();` 获取队列剩余元素个数。

```cpp
#include<bits/stdc++.h>
using namespace std;
queue<int> q;
int main(){
	q.push(1);
	q.push(10);
	q.push(121);
	q.pop();//弹出的是1(队头)
	int x=q.front();//获取的是10(当前队头) 
	cout<<x<<" "<<q.size();
	return 0;
} 
```

（才看见 C++ 是英语版，调成中文调了五分钟，找不到。。。

teacher：不要用 `endl`，它太慢了，这就是前辈~~石梯~~堆积出的教训。

又到了快乐的手搓数据结构时间：

```cpp
#include<iostream>
using namespace std;
struct queue{
	int a[1010];
	int head=1,tail=0;
	int push(int x){
		tail++;
		a[tail]=x;//向队尾添加 
	}
	void pop(){
		head--;//移一下队头即可 
	}
	int size(){
		return tail-head+1;//算大小 
	}
	int front(){
		return a[head];//返回队头 
	}
};
int main(){
	
	return 0;
} 
```

**栈**更简单，是个先进后出的东西，但是~~这个颓物不会单调栈~~。定义栈只用 `stack<栈元素类型> 变量名;` 即可。（设这个栈叫 `s`）函数有：`s.push(x);` 加入，`s.pop();` 弹出，`s.top();` 返回栈顶，`s.size();` 返回大小。

递归（dfs）实际上就是栈来实现的，回溯机制就是弹出栈顶。当 S 循环或栈空间不够的时候就会爆栈。

（666，老师讲到一半话筒炸了。

当然，如果想开大栈空间，只需要 ~~Deepseek~~ 一下就行了。

（好家伙，谷又炸了。

**单调队列** 就是个单调递增或单调递减的。它的原理就是如果加上一个数之后它不单调了，就把他删去，一直删到单调为止。

代码的话我们可以手搓，需要控制 `tail` 的位置，但如果想偷懒就可以写个 `deque<int> dq;`（双端队列）。

代码（deque)：

```cpp
deque<int> dq;
int a[maxn];
void push(int i){
	while(dq.size>0&&a[dq.back()]>=a[i])//一定先判断队列是否为空，这个应该是单调递增的代码
		a.pop_back();
	dq.push_back(i);
}
```

但是：双端队列非常慢，不建议在数据大的时候用。

但是，如果不仅单调队列，还左右端点到处移动的东西，我们就可以用双指针（$O(n)$)。

典型例子：[P1886](https://www.luogu.com.cn/problem/P1886)，上上次集训 S 活做不出的那个。

老师：单调栈这个东西没用，一点用都没有。

但是这个题讲的还有大双指针。

双指针大代码：

```cpp
#include<bits/stdc++.h>//不太知道这是什么，应该是双指针吧。。。
using namespace std;
int n,m;
int a[1000010]; 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	cin>>m;
	int sum=0;
	for(int l=1,r=1;l<=n;l++){
		while(sum<=m&&&r<=n){
			sum+=a[r];
			r++;
		}
		if(sum>m){
			r--;
			sum-=a[r];
		}
		ans=max(ans,r-l);//包含：a[l]~a[r-1] 
	}
} 
```

下课看了一圈，好像只有三个女生（包括我在内）。

### 堆：

**堆**比前两个东东都复杂，有大小根堆之分。

大根堆的声明方法是 `priority_queue<堆的数据类型> 变量名;`，有三个基本操作（设这个堆为 `p`）：插入一个数 `p.push();`，删除最大值 `p.pop();`，获取堆中最大元素 `q.top();`，询问堆中剩余元素 `q.size();`，跟栈的一模一样。小根堆最简单的声明方法就是在大根堆存数的时候把数弄成它的相反数（取相反数）。

有点题总是为难你，让你把数据类型设成个结构体。但是这东西不可能过编译，所以我们要用重载运算符。

```cpp
struct rec{
	int a,b;
};
bool operator<(const rec &x,const rec &y){
	return x.a+x.b>y.a+y.b;//把结构体放进STL比大小只能重载小于号 
}
```

手写堆则需要用二叉树（完全二叉树），最好的写法是用编号关系写（左儿子 $2i$，右儿子 $2i+1$，父亲 $\frac{i}{2}$  下取整），所以插入就得这么写：

```cpp
void push(int x){//插入 
		n++;
		a[n]=x;
		while(p!=1){
			if(a[p]>a[p/2]){//判断是否大于父亲 
				swap(a[p],a[p/2]);//用儿子代替父亲（挺好笑） 
				p=p/2;
			}
			else break;
		}
	}
```

如果我们要加快它的速度，就可以用能代替除的运算符右移（`>>`），特别快。（左移：`<<`，右移：`>>`， $1$（`>>1`）代替）。所以最终所有代码就是这样的：

```cpp
struct heap{
	int a[1010];//存堆的每个元素 
	int n=0;//堆的元素个数 
	int top(){//最大值 
		return a[1];
	}
	void push(int x){//插入 
		n++;
		int p=n;
		a[n]=x;
		while(p!=1){
			if(a[p]>a[p>>1]){//判断是否大于父亲 
				swap(a[p],a[p>>1]);//用儿子代替父亲 
				p=p>>1;
			}
			else break;
		}
	}
	void pop(){//删除最大值 
		swap(a[1],a[n]);
		n--;//删了
		int s=1;
		while((p<<1)<=n){
			int l=s<<1;//左儿子(=s*2)
			int r=l|1;//右儿子(=s*2+1)
			int ss=s;
			if(r<=n/*可能没有右儿子*/&&a[r]>a[l]) ss=r;//ss一定是两个儿子中较大的 
			if(a[ss]>a[s]){
				swap(a[ss],a[s]);
				s=ss;
			}
			else break; 
		} 
	}
	int size(){//还有几个数 
		
	} 
};
```

teacher：我们终于可以用一下 PPT 了啊。

例题：[P3528](https://www.luogu.com.cn/problem/P3528)。

~~关于老师一个上午讲一天半的知识这件事~~

### 并查集：

**并查集**中的每个元素都可以看成一个集合，它们都有一个指向自己的指针，如果想把元素 $1$ 与 $2$ 合并，就把 $1$ 的指针指向 $2$ 就行了，合并两个集合要注意不能孤立元素。

代码：

```cpp
int to[maxn];//to[i]：i的箭头指向谁
int go(int p){//走向哪里 
	if(p==to[p]) return p;
	else return go(to[p]);
} 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) to[i]=i;
	//合并
	to[go(p1)]=go(p2); 
	//查询
	go(p1)=go(p2); 
}
```

但是这样写并查集就有可能退化成一条链，所以我们可以用路径压缩，按秩合并和随机合并优化它。

```cpp
//路径压缩 
int to[maxn];//to[i]：i的箭头指向谁
int go(int p){//走向哪里 
	if(p==to[p]) return p;
	else{
		to[p]=go(to[p]);
		return to[p]; 
	}
} 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) to[i]=i;
	//合并
	to[go(p1)]=go(p2); 
	//查询
	go(p1)=go(p2); 
}
```
按秩合并和随机合并因为~~我太懒了~~所以就不写了，正儿八经的优化就是路径压缩，就写这玩意就可以了，那俩不一定对，别用。

```cpp
#include<bits/stdc++.h>//某一例题（没记上）的代码
using namespace std;
int main() {
	cin>>n;
	for(int i=1;i<=n;i++){
		to[i]=i;
	}
	for(int i=m;i>=1;i--){//倒着来 
		int l,r,x;
		cin>>l>>r>>x;
		int p=go(l);//go(i)从i向右第一个没被染色的位置 
		while(p<=r){//当前位置还在区间内 
			a[p]=x;//染色
			int np=b=go(p+1);
			to[p]=go(r+1);
			p=np; 
		}
	}
	return 0;
} 
```
ee，讲得我脑袋疼。

#### -- 下午 --

### 字典树,Trie：
先来个例题：

$N$  $行N$ 列的点阵 $k$ 个特殊点 $(x_i,y_i)$ 安全性$w(a,b)=\min(|a-x_i|+|b-y_i|)$ 求一条从 $(1,1)$ 到 $(n,n)$ 的路径最大化路径上安全性的最小值要求平方算法。

第一步：弄着一个 BFS 队列，此时已经把每个点的安全值排好序了。接着我们发现：从起点到终点跟从终点到起点没有一点区别。这样只需要~~写下代码~~即可。

```cpp
#include<bits/stdc++.h>
using namespace std;
struct node{
	int nxt[2];//nxt[0],nxt[1]：从当前点走0和1会走到那里，走到零代表这个节点不存在 
	node(){
		nxt[0]=xnt[1]=0
	}
}z[10010];
void inssert(int x){
	for(int i=30;i>=0;i--){
		int y=(x>>i)&1;//取出x的二进制的第i位 
		if(z[p].nxt[y]==0){
			cnt++;
			z[p].nxt[y]=cnt;
		}
		p=z[p].nxt[y];
	}
} 
int query(int x){//从trie中找一个数，使它与x异或后最大 
	int p=root,ans=0;
	for(int i=30;i>=0;i--){
		int y=(x>>i)&1;
		if(z[p].nxt[y^1]!=0)  ans=ans|(1<<i),p=z[p].nxt[y^1];
	}
	return ans;
}
int main(){
	root=1;
	return 0;
} 
```

### 分块：

**分块**一定能解决线段树能解决的问题。它的意思是原来有 $n$ 个数，分块能把它分成一块一块的，若每块长度为 $s$，则有 $\frac{n}{s}$ 块。为了保证时间复杂度，所以我们分 $\sqrt{n}$ 个块。

这东西很不好写，代码如下：

```cpp
#include<bits/stdc++.h>//zhx 原代码
#define int long long
#define maxn 10000010
using namespace std;
int belong[maxn];//belong[i] 代表第i个数属于第几块 
int sum[maxn];//sum[i] 代表第i块的和是多少 
int daxiao[maxn];//daxiao[i] 代表第i块的大小是多少 
int col[maxn];//col[i] 代表第i块被整体加了col[i] 
int main()
{
	cin >> n >> m;
	for (int i=1;i<=n;i++)
		cin >> a[i];
	int s = sqrt(n);//每块的大小 
	for (int i=1;i<=n;i++)
		belong[i] = i/s+1;
	for (int i=1;i<=n;i++)
	{
		sum[belong[i]] += a[i];
		daxiao[belong[i]] ++;
	}
		
	for (int x=1;x<=m;x++)
	{
		int opt;
		cin >> opt;
		if (opt == 1)//询问操作
		{
			int l,r;
			cin >> l >> r;
			int ans=0;
			if (belong[l] == belong[r])
				for (int i=l;i<=r;i++)
					ans += a[i] + col[belong[i]];
			else
			{
				for (int i=l;belong[i] == belong[l]; i++)
					ans += a[i] + col[belong[i]];
				for (int i=r;belong[i] == belong[r]; i--)
					ans += a[i] + col[belong[i]];
				for (int i=belong[l] + 1; i < belong[r]; i++)
					ans += sum[i];
			}
			cout << ans << "\n";
		} 
		else
		{
			int l,r,v;
			cin >> l >> r >> v;
			if (belong[l] == belong[r])
				for (int i=l;i<=r;i++)
					a[i] += v;
			else
			{
				for (int i=l;belong[i] == belong[l]; i++)
					a[i] += v,sum[belong[i]] += v;
				for (int i=r;belong[i] == belong[r]; i--)
					a[i] += v,sum[belong[i]] += v;
				for (int i=belong[l] + 1; i < belong[r]; i++)
				{
					sum[i] += v * daxiao[i];
					col[i] += v; 
				}
			}
		}
	}
	return 0;
}
```
### 莫队

代码：
```cpp
#include<bits/stdc++.h>
using namespace std;
struct node{
	int l,r,id,ans;
}q[10010];
void ins(int x){
	//if(cnt[x]==0) ans++;
	cnt[x]++;
	if(cnt[x]%2==0) ans++;
	else{
		if(cnt[x]!=1)ans--;
	} 
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=m;i++){
		cin>>q[i].l>q[i].r;
		q[i].id=i;
	}
	for(int i=1;i<=m;i++){
		int l=q[i].l,r=q[i].r;
		memset(cnt,0,sizeof(cnt));
		ans=0;
		for(int j=l;j<=r;j++)
			ins(a[i]);
		q[i].ans=ans;
	}
	return 0;
}
```
但是这样时间复杂度就太高了，所以我们优化亿下：

```cpp
#include<bits/stdc++.h>
using namespace std;
struct node{
	int l,r,id,ans;
}q[10010];
void ins(int x){
	//if(cnt[x]==0) ans++;
	cnt[x]++;
	if(cnt[x]%2==0) ans++;
	else{
		if(cnt[x]!=1)ans--;
	} 
}
void del(int x){
	cnt[x]--;
	if(cnt[x]!=0){
		if(cnt[x]%2==0) ans++;
		else ans--;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=m;i++){
		cin>>q[i].l>q[i].r;
		q[i].id=i;
	}
	for(int i=q[1].l;i<=q[1].r;i++){
		ins(a[i]);
	}
	q[1].ans=ans;
	for(int i=1;i<=m;i++){
		int l1=q[i-1].l,r1=q[i-1].r;
		int l2=q[i].l,r2=q[i].r;
		if(l1<l2){
			for(int i=l1;i<l2;i++){
				del(a[i]);
			}
		}
		else{
			for(int i=l2;i<l1;i++)
				ins(a[i]);
		}
		if(r1<r2){
			for(int i=r1+1;i<=r2;i++){
				ins(a[i]);
			}
		}
		else{
			for(int i=r2+1;i<=r1;i++){
				ins(a[i]);
			}
		}
		q[i].ans=ans;
	}
	return 0;
}
```
但这个的时间复杂度还是 $O(n^2)$，所以我们再加上死亡分块：

```cpp
#include<bits/stdc++.h>
#define maxn 10010
using namespace std;
int n,m,a[maxn]; 
int belong[maxn],cnt[maxn];
int ans;
struct node{
	int l,r,id,ans;
}q[10010];
bool operator<(const node &x,const node &y){
	return x.l+x.r>y.l+y.r;
}
bool cmp1(const node &q1,const node &q2){
	if(belong[q1.l]!=belong[q2.l]) return belong[q1.l]<belong[q2.l];
	else return q1.r<q2.r;
}
bool cmp2(const node &q1,const node &q2){
	return q1.r<q2.r;
}
void ins(int x){//插入 
	//if(cnt[x]==0) ans++;
	cnt[x]++;
	if(cnt[x]%2==0) ans++;
	else if(cnt[x]!=1)ans--;
}
void del(int x){//删除 
	cnt[x]--;
	if(cnt[x]!=0){
		if(cnt[x]%2==0) ans++;
		else ans--;
	}
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=m;i++){
		cin>>q[i].l>>q[i].r;
		q[i].id=i;
	}
	int s=sqrt(n);
	for(int i=1;i<=n;i++){
		belong[i]=i/s+1;
	}
	sort(q+1,q+m+1,cmp1);
	for(int i=q[1].l;i<=q[1].r;i++){
		ins(a[i]);
	}
	q[1].ans=ans;
	for(int i=2;i<=m;i++){
		int l1=q[i-1].l,r1=q[i-1].r;
		int l2=q[i].l,r2=q[i].r;
		if(l1<l2){
			for(int i=l1;i<l2;i++){
				del(a[i]);
			}
		}
		else{
			for(int i=l2;i<l1;i++)
				ins(a[i]);
		}
		if(r1<r2){
			for(int i=r1+1;i<=r2;i++){
				ins(a[i]);
			}
		}
		else{
			for(int i=r2+1;i<=r1;i++){
				ins(a[i]);
			}
		}
		q[i].ans=ans;
	}
	sort(q+1,q+m+1,cmp2);
    for (int i=1;i<=m;i++)
		cout<<q[i].ans<<"\n";
	return 0;
}
```
累 S 了，还不一定对。。。（19:34 pm：改吐了，终于对了。。。

dalao1：“哎我跟你说 zhx 的代码是错的。”

dalao2：“啊？”

dalao1：“我看见了三个错误，你看...”

### 分治：

**分治**就是分而治之...（讲了至少五遍了

我们可以用它算逆序对。

代码：

```cpp
void merge(int l,int r){//l~r之间共有多少个逆序对 
	if(l==r) return;
	int m=(l+r)>>1;//=l+r/2
	merge(l,m);//递归算左区间（l~m）的答案 ，a[l]~a[m]排好序了 
	merge(m+1,r);//递归算右区间（m+1~r）的答案 ，a[m+1]~a[r]排好序了 
	for(int i=1;i<=r;i++){
		if(p1>m)b[i]=a[p2],p2++;
		else if(p2>r)b[i]=a[p1],p1++; 
		else if(a[p1]<=a[p2]) b[i]=a[p1],p1++;
		else b[i]=a[p2],p2++,ans+=m-p1+1;
	}
	for(int i=1;i<=r;i++){
		a[i]=b[i];
	}
}
```

老例题：[P9753](https://www.luogu.com.cn/problem/P9753)。

老师：这个题我们可以用栈。

全班：哦————！

这个题可以把字符存进栈里，然后操作就会简单一点（瞎写ing

（好家伙，第一天就有这么多，看来这次笔记得分批了。。。
## Day 2：
今天会有多少呢？
#### -- 上午 --
### 线段树：
teacher：线段树占数据结构的 $90 \%$，它没有莫队负责，但它能玩的花样太多了。

线段树可以用来解决针对区间的操作的问题。线段树的每一个结点都是一个区间，只要长度不是 $1$，那么我们就可以一直往下分，所以最后一层的结点都只有一个元素。它的每两个儿子结点都可以看成平分了它们的父亲。这是线段树的基础结构（当 $n=8$ 时）：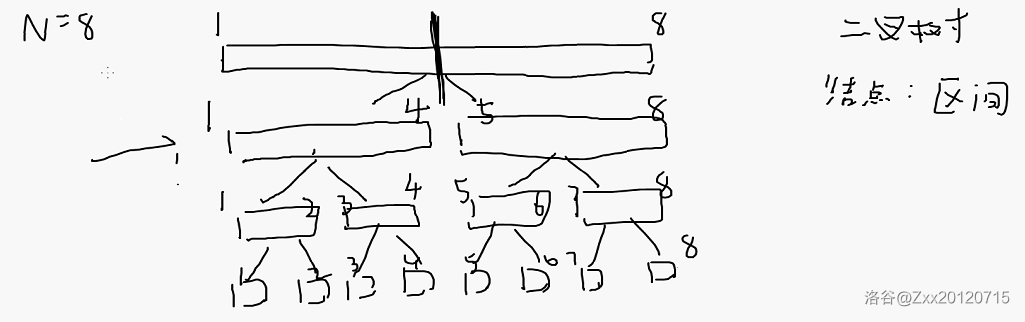

![](https://cdn.luogu.com.cn/upload/image_hosting/ayo7y6fj.png)

线段树有  $logn$ 层，本身是分治的方法。线段树有 $2n$ 个结点，应该是因为有点类似满二叉树。它的思路很像分治。

如果你想计算一个结点（区间）的信息，方法是用它的左右儿子区间合并的结果。这就是线段树最基础的方法——求和。

如果我们要询问一段区间的和，只需要把这段区间的值拿出来求和就行。但是要是这一段区间没分成一个节点，那么我们就要用更多的结点（区间）拼成一个更大的区间，再求和。

注意：每一层的区间最多有两个，如果多于两个，那么就能合并了。

代码：

```cpp
#include<bits/stdc++.h>//WA+RE的线段树1
#define maxn 100010
#define lson l,mid,rt<<1 //左儿子(=rt*2)
#define rson mid+1,r,rt<<1|1 //右儿子 (=rt*2+1) 位运算提速度
#define root 1,n,1 
using namespace std;
int n,m;
int a[100010];

struct node{//一个线段树节点  
	int sum;//区间和
	int siz;//区间长度 
	int add;//懒标记，代表这个区间被整体加了多少
	node(){
		sum=siz=add=0;
	} 
	void init(int v){//用一个数初始化 
		sum=v;
		siz=1;
	}
}z[maxn<<2];//z[i]表示线段树的第i个结点，注意开四倍空间

node operator+(const node &l,const node &r){//重载运算符(加法)
	node res;
	res.sum=l.sum+r.sum;
	res.siz=l.siz+r.siz;
	return res;
}

void color(int l,int r,int rt,int v){//给l,r,rt这个节点打一个+v的懒标记 
	z[rt].add+=v;
	z[rt].sum+=z[rt].siz*v; 
}

void pus(int l,int r,int rt){//把懒标记下放（告诉儿子）
	if(z[rt].add==0) return;//没标记，不用下放，可以不写 
	int mid=(l+r)>>1;
	color(lson,z[rt].add);
	color(rson,z[rt].add);
	z[rt].add=0;
}

void build(int l,int r,int rt){//建树（初始化l,r,rt这个节点） 
	//编号为rt的线段树结点所对应的区间为l~r 
	if(l==r){
		z[rt].init(a[l]);
		return; 
	} 
	int mid=(l+r)>>1;//(l+r)/2
	build(lson);
	build(rson);
	//合并 
	z[rt]=z[rt<<1]+z[rt<<1|1];
}

node query(int l,int r,int rt,int nowl,int nowr){//查询(只返回这段区间的信息)
    //l,r,rt:一个节点 nowl,nowr:询问区间的左端点和右端点 
	if(nowl<=l&&r<=nowr) return z[rt];
	pus(l,r,rt);
	int mid=(l+r)>>1;
	if(nowl<=mid){//与左右儿子是否有交 
		if(mid<nowr) return query(lson,nowl,nowr)+query(rson,nowl,nowr);
		else return query(lson,nowl,nowr);
	}
	else return query(rson,nowl,nowr);
}

void modify(int l,int r,int rt,int nowl,int nowr,int v){//修改 （要修改所有有要改元素的区间） 
	//把nowl~nowr这段区间整体+v
	if(nowl<=l&&r<=nowr){//当前线段树结点被修改区间整体包含 
		color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记 
		return;
	} 
	pus(l,r,rt);
	int mid=(l+r)>>1;
	if(nowl<=mid) modify(lson,nowl,nowr,v);
	if(mid<nowr) modify(rson,nowl,nowr,v);
	z[rt]=z[rt<<1]+z[rt<<1|1];
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(root);//root：根节点，编号为1 
	cin>>m;
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		if(opt==1){//询问 
			int l,r;
			cin>>l>>r;
			cout<<query(root,l,r).sum<<"\n";
		}
		else{
			int l,r,v;
			cin>>l>>r>>v;
			modify(root,l,r,v);
		}
	}
	return 0;
} 
```
如果出题人~~针对你~~，换一种方式修改和询问，那么代码就是：

```cpp
#include<bits/stdc++.h>//还是没补全
#define maxn 100010
#define lson l,mid,rt<<1 //左儿子(=rt*2)
#define rson mid+1,r,rt<<1|1 //右儿子 (=rt*2+1) 位运算提速度
#define root 1,n,1 
using namespace std;
int n,m;
int a[100010];

struct node{//一个线段树节点  
	int sum;//区间和
	int minn,maxx;//区间最小值，区间最大值
	int siz;//区间长度 
	int add;//懒标记，代表这个区间被整体加了多少
	node(){
		sum=siz=add=maxx=minn=0;
	} 
	void init(int v){//用一个数初始化 
		sum=minn=maxx=v;
		siz=1;
	}
}z[maxn<<2];//z[i]表示线段树的第i个结点，注意开四倍空间

void color(int l,int r,int rt,int v){//给l,r,rt这个节点打一个+v的懒标记 
	z[rt].add+=v;
	z[rt].sum+=z[rt].siz*v; 
	z[rt].maxx+=v;
	z[rt].minn+=v;
}

node operator+(const node &l,const node &r){//重载运算符(加法)
	node res;
	res.sum=l.sum+r.sum;
	res.siz=l.siz+r.siz;
	res.minn=min(l.minn,r.minn);
	res.maxx=max(l.maxx,r.maxx);
	return res;
}

void modify(int l,int r,int rt,int nowl,int nowr,int v){//修改 （要修改所有有要改元素的区间） 
	//把nowl~nowr这段区间整体+v
	if(nowl<=l&&r<=nowr){//当前线段树结点被修改区间整体包含 
		color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记 
		return;
	} 
	pus(l,r,rt);
	int mid=(l+r)>>1;
	if(nowl<=m) modify(lson,nowl,nowr,v);
	if(m<nowr) modify(rson,nowl,nowr,v);
	z[rt]=z[rt<<1]+z[rt<<1|1];
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(root);//root：根节点，编号为1 
	cin>>m;
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		if(opt==1){//询问 
			int l,r;
			cin>>l>>r;
			cout<<query(root,l,r).sum<<"\n";
		}
		else{
			int l,r,v;
			cin>>l>>r>>v;
		}
	}
	return 0;
} 
```
如果询问又弄成了一堆绝对值什么玩意相加，那么：

```cpp
#include<bits/stdc++.h>
#define maxn 100010
#define lson l,mid,rt<<1 //左儿子(=rt*2)
#define rson mid+1,r,rt<<1|1 //右儿子 (=rt*2+1) 位运算提速度
#define root 1,n,1 
using namespace std;
int n,m;
int a[100010];

struct node{//一个线段树节点  
	int sum;//区间相邻两数差的绝对值 
	int add;//懒标记，代表这个区间被整体加了多少
	int lv,rv;//最左边和最右边的数 
	node(){
		sum=add=0;
	} 
	void init(int v){//用一个数初始化 
		sum=0;
		lv=rv=v;
		siz=1;
	}
}z[maxn<<2];//z[i]表示线段树的第i个结点，注意开四倍空间

void color(int l,int r,int rt,int v){//给l,r,rt这个节点打一个+v的懒标记 
	z[rt].add+=v;
	z[rt].lv+=v;
	z[rt].rv+=v;
}

node operator+(const node &l,const node &r){//重载运算符(加法)
	node res;
	res.sum=l.sum+r.sum+abs(l.rv-r.lv);
	res.lv=l.lv;
	res.rv=r.rv;
	return res;
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(root);//root：根节点，编号为1 
	cin>>m;
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		if(opt==1){//询问 
			int l,r;
			cin>>l>>r;
			cout<<query(root,l,r).sum<<"\n";
		}
		else{
			int l,r,v;
			cin>>l>>r>>v;
			modify(root,l,r,v);
		}
	}
	return 0;
} 
```
再来一问：从  $a_l^2$ 加到 $a_r^2$ 又能怎样？

```cpp
//没写代码，待会补吧。。。
```

终于等到了：线段树2！

![](https://cdn.luogu.com.cn/upload/image_hosting/4a17kajg.png)

```cpp
#include<bits/stdc++.h>//补全是不可能的
#define maxn 100010
#define lson l,mid,rt<<1 //左儿子(=rt*2)
#define rson mid+1,r,rt<<1|1 //右儿子 (=rt*2+1) 位运算提速度
#define root 1,n,1 
using namespace std;
int n,m;
int a[100010];

void color(int l,int r,int rt,int v){//给l,r,rt这个节点打一个+v的懒标记 
	z[rt].add+=v;
	z[rt].sum+=z[rt].siz*v; 
}

node operator+(const node &l,const node &r){//重载运算符(加法)
	node res;
	res.sum=l.sum+r.sum;
	res.siz=l.siz+r.siz;
	return res;
}

void modify(int l,int r,int rt,int nowl,int nowr,int v){//修改 （要修改所有有要改元素的区间） 
	//把nowl~nowr这段区间整体+v
	if(nowl<=l&&r<=nowr){//当前线段树结点被修改区间整体包含 
		color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记 
		return;
	} 
	pus(l,r,rt);
	int mid=(l+r)>>1;
	if(nowl<=m) modify(lson,nowl,nowr,v);
	if(m<nowr) modify(rson,nowl,nowr,v);
	z[rt]=z[rt<<1]+z[rt<<1|1];
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(root);//root：根节点，编号为1 
	cin>>m;
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		if(opt==1){//询问 
			int l,r;
			cin>>l>>r;
			cout<<query(root,l,r).sum<<"\n";
		}
		else{
			int l,r,v;
			cin>>l>>r>>v;
		}
	}
	return 0;
} 
```
又来了：线段树，一个区间，问你子区间的最大和是多少。这东西是个最大子段和，balabala...

#### -- 下午 --
### 可持久化线段树：
（终于不讲线段树了...不对，这还是线段树。。。

设第 $i$ 个时刻有一棵线段树，第 $i+1$ 时刻时某一元素被改变，那么包含此元素的链都会受到影响。但是 $i$ 和 $i+1$ 时刻只有这一条链受到了改变，共有 $logn$ 个结点变了。此时我们可以把这条链新建下来，我们就会缺失一些左儿子或右儿子（没发生变化的），那么我们用原来线段树的左儿子右儿子连上那条链，就可以把这些缺失的东西都补上了（有点抽象，看图吧）。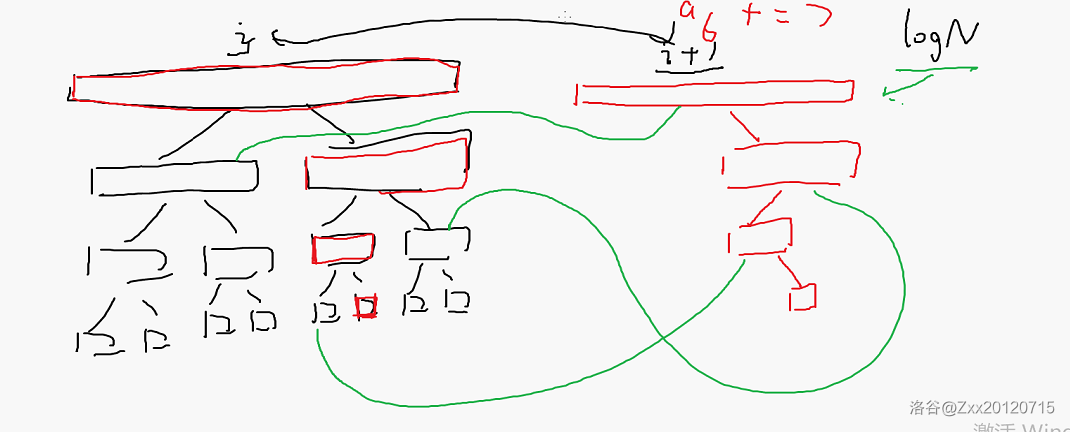

![](https://cdn.luogu.com.cn/upload/image_hosting/00xn33hw.png)

所以我有了一棵新的线段树，但建树只用了 $logn$ 的时间，这就是可持久化线段树。

洛谷上没有正儿八经的可持久化线段树板子题，所以还是不弄例题了吧。

代码：

```cpp
#include<bits/stdc++.h>//错误连篇的可持久化线段树谁能拒绝呢？
#define maxn 100010
using namespace std;
int cnt;//节点总数 
int n,m,a[maxn],root[maxn];

struct node{
	int l,r;//左右儿子编号 
	int sum;//区间和 
	node(){
		l=r=sum=0;
	} 
}z[maxn*logn];

void update(int p){
	z[p].sum=z[z[p].l]+z[z[p].r].sum;
}

int build(int l,int r){//当前区间为l~r 是这段区间对应的结点编号 
	cnt++;
	int p=cnt;
	if(l==r){
		z[p].sum=a[l];
		return;
	} 
	int mid=(l+r)>>1;
	z[p].l=build(l,mid);
	z[p].r=build(mid+1,r);
	update(p);
	return p;
}

int query(int l,int r,int rt,int nl,int nr){
	if(nl<=l&&r<=nr) return z[rt].sum;
	int mid=(l+r)>>1;
	if(nl<=mid){
		if(mid<nr) return query(l,mid,z[rt].l,nl,nr)+query(mid+1,r,z[rt].r,nl,nr);
		else return query(l,mid,z[rt].l,nl,nr);
	}
	else query(mid+1,r,z[rt].r,nl,nr);
}

int modify(int l,int r,int rt,int p,int v){//注意可持久化 
	//当前线段树编号为rt，对应区间为l~r，要把a[p]+=v 
	cnt++;
	int q=cnt;//新建节点，用于修改 
	z[q]=z[rt];
	if(l==r){
		z[q].sum+=v;
		return;
	}
	int mid=(l+r)>>1;
	if(p<=mid){//左儿子 
		z[q].l=modify(l,mid,z[q].l,p,v);
	}
	else z[q].r=modify(mid+1,r,z[q].r,p,v);
	update(q);
	return q; 
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i]; 
	cin>>m;
	root[0]=build(1,n);//root[i]表示第i次操作后根节点为几
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		if(opt==1){
			int p,v;
			cin>>p>>v;
			root[i]=modify(1,n,root[i-1],p,v);
		}
		else{
			int k,l,r;
			cin>>k>>l>>r;
			cout<<query(1,n,root[k],l,r)<<"\n";
			root[i]=root[i-1];//可以访问所有的历史线段树 
		}
	} 
	return 0;
}
```

当然，这还有一个更拓展的东西——可持久化权值线段树（前缀值域可持久化线段树），也叫主席树。前缀就是要维护 $n+1$ 棵线段树。

[e...](https://oi-wiki.org/ds/persistent-seg/#%E4%B8%BB%E5%B8%AD%E6%A0%91)

代码：

例题：[P3834](https://www.luogu.com.cn/problem/P3834)

老师：洛谷起名起的不对。

### 根号分治：
根号分治，分而治之，是一个更严格的分块，它可以把大小问题分开解答。