题解：P4179 [CQOI2010] 鼹鼠

这个题看上去十分吓人，实际上并不是很难。

首先，该如何建图呢？

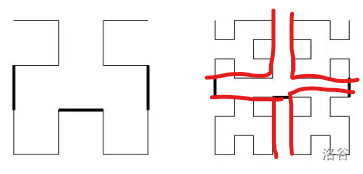
如图，第 $i$ 个图形是由四个 $i-1$ 号图形拼成的。这样就可以建图了。

下一步，我们要求出每个格子水深。

每一个格子的水可以往上下左右四个方向流，所以我们从最顶上一排的格子往下 dfs，就可以求出每个各自的水深了。这里只讲往右流的情况。

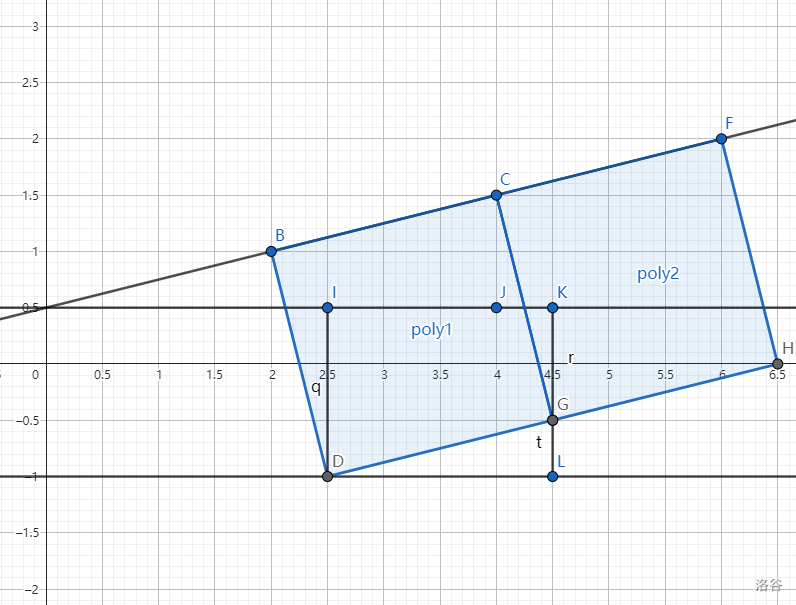
如图，图中 $\angle GDL = \alpha$。左边正方形水深 $ID$, 右边正方形水深 $KG$。根据简单的三角函数，$KG=ID-\sin \alpha$。

最后，求出所有正方形被水淹没的面积即可。

代码：

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
typedef long long ll;
typedef double ld;

const ll Pig = 5e3 + 10;
const ld Pi = acos(-1), eps = 1e-10;

bitset<Pig> hole[Pig], cur[Pig], vis[Pig];
ld cs, sn, ans = 0;
ll n, alpha, len = 1;

void dfs(ll i, ll j, ld height) {
    if (i == 0 or j == 0 or i > len or j > len)
        return;
    if (!hole[i][j])
        return;
    if (vis[i][j])
        return;
    if (height <= eps)
        return;
    height = min(height, sn + cs);
    vis[i][j] = 1;
    if (!alpha)
        ans += 1;
    else {
        if (alpha > 45)
            swap(sn, cs);
        if (height <= sn)
            ans += height * height;
        else if (height <= cs)
            ans += (2 * height - sn) * sn;
        else
            ans += (2.0 * sn * cs) - (sn + cs - height) * (sn + cs - height);
        if (alpha > 45)
            swap(sn, cs);
    }
    dfs(i + 1, j, height + cs);
    dfs(i - 1, j, height - cs);
    dfs(i, j - 1, height - sn);
    dfs(i, j + 1, height + sn);
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.setf(ios::fixed);
    cout.precision(6);
    cin >> n >> alpha;
    cur[1][1] = 1;
    hole[1][1] = 1;
    for (ll round = 2; round <= n; round++) {
        for (ll i = 1; i <= len; i++) {
            for (ll j = 1; j <= len; j++) {
                hole[len - j + 1][i] = hole[j][((len + 1) << 1) - i] = (!cur[i][j]);
                hole[len + i + 1][j] = hole[len + i + 1][len + j + 1] = cur[i][j];
            }
        }
        for (ll i = 1; i <= 2 * len + 1; i++) hole[len + 1][i] = 1;
        for (ll i = 1; i <= len; i++) hole[i][len + 1] = 1;
        len = ((len << 1) | 1);
        for (ll i = 1; i <= len; i++) {
            for (ll j = 1; j <= len; j++) {
                cur[i][j] = hole[i][j];
            }
        }
    }
    ld al = 1.0 * alpha * Pi / 180.0;
    cs = cos(al);
    sn = sin(al);
    for (ll i = 1; i <= len; i++) dfs(1, i, cs);
    if (alpha > 0)
        ans /= (2.0 * cs * sn);
    printf("%0.6lf", ans);
    return 0;
}