线段树学习笔记 - 洛谷保存站

线段树，是一种可以在 $O(\log n)$ 的时间复杂度内处理可合并性信息的区间修改与区间查询的数据结构。

> [P3372](https://www.luogu.com.cn/problem/P3372)：有一个长度为 $n$ 的数列 $a$，要支持将一段区间的每一个数加上 $k$，或者查询一段区间的和。$n \le 10^5$。

### 基本结构

以模板为例，线段树是一种二叉树的结构，树上的每个结点代表数列的一段区间。对于一个结点，设它代表的区间为 $[l,r]$，如果 $l<r$，即这段区间不只有一个元素，则它有两个子结点，分别代表 $[l,mid]$ 和 $[mid+1,r]$，其中 $mid=\frac{l+r}{2}$ 取整。

线段树的表示方法采取二叉树在序列上的表示方法，即对于一个结点 $u$，它的两个子结点分别是 $2u$ 和 $2u+1$。根结点的编号为 $1$，代表的区间为 $[1,n]$。

下图是对于一个长度为 $10$ 的数列建立的线段树：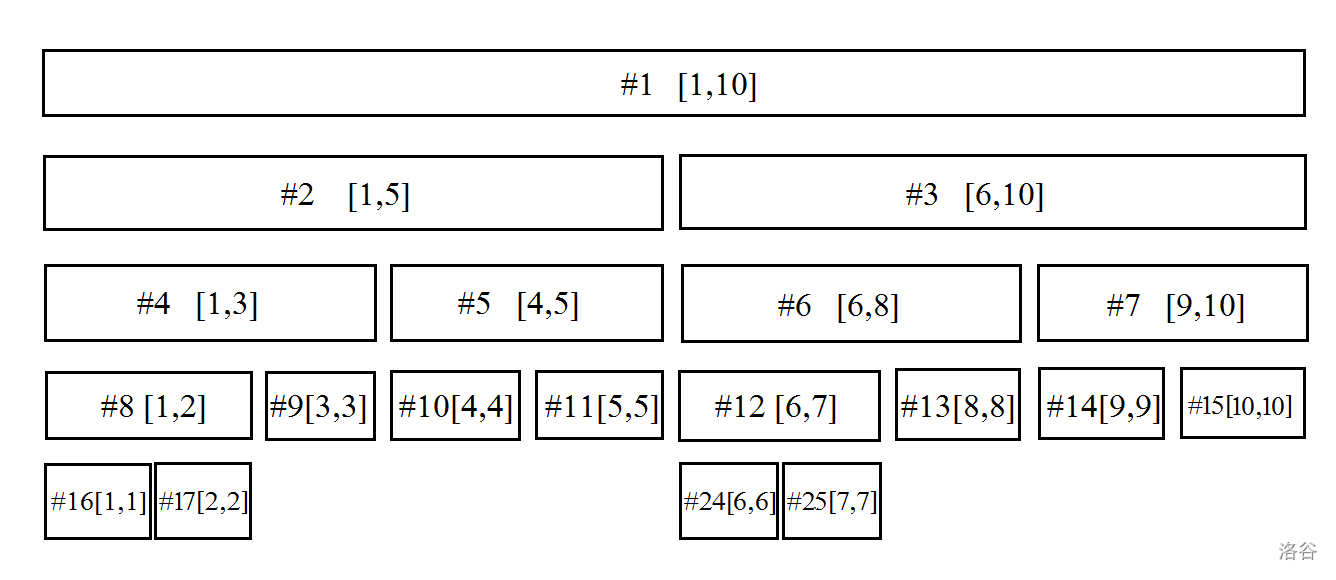

![](https://cdn.luogu.com.cn/upload/image_hosting/lep45bgv.png)

其中带 `#` 的是结点编号，中括号内的是该结点代表的区间。每条“线段”下方的两条线段是它的两个子结点。根据线段树的结构性质，这个结点代表的区间和等于它两个子结点值的和。

区间中只有一个元素（左右端点相同）的线段被称为元线段，没有子结点。

定义 $s_u$ 为结点 $u$ 所代表的区间和，则有 $\operatorname{pushup}(u)$ 函数：

```cpp
void pushup(int u){
	s[u]=s[u*2]+s[u*2+1];
}
```

同时我们有建立线段树的代码：

```cpp
void build(int u,int l,int r) {
	L[u]=l,R[u]=r;//结点 u 代表的区间左右端点
	if(l==r)s[u]=a[l];
	else {
		build(u*2,l,(l+r)/2);
		build(u*2+1,(l+r)/2+1,r);
		pushup(u);
	}
}
```

发现线段树最多有 $\log_2 n$ 层，所以线段树的结点编号不超过 $4n-1$。

### 区间查询

```cpp
void dfs(int u){
	if(L[u]==R[u])return ;
	s[u];
	dfs(u*2),dfs(u*2+1);
}
//这样可以遍历线段树中的所有线段
```

区间查询（$[l,r]$）在线段树上首先可以表现为 $[l,l] \sim [r,r]$ 这一堆元线段的和。在线段树上递归查询，复杂度最大可以达到 $O(n \log n)$。

因为一个结点的所有孩子的区间一定都是它自己的子区间，所以如果一个结点代表的区间与目标区间完全不相交，就没必要递归下去了（直接返回 `0`）。

如果一个结点代表的区间完全覆盖在目标区间里，那么接下来从这里的递归就都是可以省略的。比如说 $L_u=1,R_u=2$，那么根据线段树的性质， $s_u=s_{2u}+s_{2u+1}$，也就是说返回当前的 $s_u$ 和接下来递归再相加结果就是一样的了。

因此，只有当前结点代表的区间有一部分在目标区间里才需要继续递归查找。

我们分析一下复杂度：在递归查询中，最多就是有两个查询（假设它们的结点编号分别是 $u$ 和 $v$），且 $L_u < l \leqslant R_u < L_v < r < R_v$，此时 $u$ 的右子结点和 $v$ 的左子结点需要继续递归（这其中隐含了一个性质，那就是线段树中的两段线段要么完全不相交，要么一个覆盖另一个，而后者不可能在同层出现）。又因为最开始只有一个 $u=1$ 的查询，所以每层最多只会新建两个递归询问。同时线段树最多 $\log_2 n$ 层，所以复杂度也是 $\log n$ 的。

```cpp
int query(int u,int l,int r) {//l 和 r 为查询的区间
	if(l<=L[u] && R[u]<=r)return s[u];
	if(l>R[u] || L[u]>r)return 0;
	pushdown(u);
	return query(u*2,l,r)+query(u*2+1,l,r);
}
```

这个 `pushdown` 是什么呢？我们接着看。

### 区间修改

我们可以仿照区间查询的想法，如果当前区间完全被需要修改的区间覆盖，则不再递归。区间修改的重点就是在这里。我们需要做一个标记，来表示我们在这里修改了。

```cpp
void maketag(int u,int k){
	len[u]=R[u]-L[u]+1;
	lzy[u]+=k,s[u]+=k*(len[u]);
}
```

定义 $lazy\_tag_u$ 表示我们在 $u$ 这个结点总共增加了多少没有向下递归的值。当我们没有需要递归到它的子结点的查询/修改时，那这个标记放在这里就够了。

如果需要向下递归，则我们需要将它的标记下放到它的子结点。此时它没有未下放的标记了，故清零。

```cpp
void pushdown(int u) {
	maketag(u*2,lzy[u]);
	maketag(u*2+1,lzy[u]);
	lzy[u]=0;
}
```

综上，我们需要在查询操作和修改操作中需要向下递归查询时下放标记。所以区间修改的代码如下：

```cpp
void update(int u,int l,int r,int k) {
	if(l<=L[u]&&R[u]<=r)maketag(u,k);
	else if(l<=R[u]&&L[u]<=r) {
		pushdown(u);
		update(u*2,l,r,k);
		update(u*2+1,l,r,k);
		pushup(u);
	}
}
```

### 标记永久化

不想下传标记怎么办？

我们可以每次修改时将当前区间的 $s_u$ 修改上 $k \cdot len_u$，然后在标记处直接加 $k$，直到当前区间完全被修改区间覆盖停止递归。

但是这样下面的区间就没有被更新，所以我们查询时要一路加上懒标记。

```cpp
void update(int u,int l,int r,long long k){
    if(l<=L[u]&&R[u]<=r)s[u]+=len[u]*k,tag[u]+=k;
    else if(l<=R[u]&&L[u]<=r){
        s[u]+=k*max(min(r,R[u])-max(l,L[u])+1,0);
        update(u<<1,l,r,k),update(u<<1|1,l,r,k);
    }
}
long long query(int u,int l,int r,long long add){
    if(l<=L[u]&&R[u]<=r)return s[u]+add*len[u];
    if(l>R[u]||L[u]>r)return 0;
    return query(u<<1,l,r,add+tag[u])+query(u<<1|1,l,r,add+tag[u]);
}
```

### 扫描线

> [P5490](https://www.luogu.com.cn/problem/P5490)：给出 $n$ 个边平行于坐标轴的矩形位置，求它们覆盖的总面积。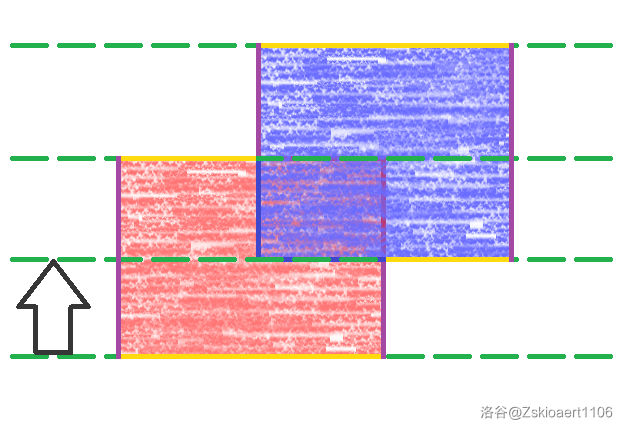

![](https://cdn.luogu.com.cn/upload/image_hosting/b0iigiag.png)

我们想象有一条线从下向上扫描。图中四条绿线将图形分割成了三个不重合的矩形，我们可以分别求出其面积。

在知道原矩形每条边的情况下，矩形的高已经有了——拿上边的横坐标减下边。如何求矩形的宽？是的，线段树。

我们维护扫描线上每段是否有矩形覆盖，元线段就取离散化后相邻的两个 $x$ 坐标。容易发现，只要元线段的值 $\geqslant 1$，就要返回这段元线段的长度。

现在的问题是怎么知道一段线段中是否所有的元线段都被覆盖，因为重复贡献同一段是没有用的，但是不计的话删除又会出问题。

这里提供两种方法。

第一种方法：标记永久化。

我们建线段树时记录这段区间真正的的长度 $len$，然后因为记录的是线段端点，所以如果 $l$ 和 $r$ 在离散化数组中还相隔元素，就继续向下建。注意这里是与维护序列的线段树不同的。

之后的修改中，如果当前区间被大区间包含就将 $tag_u$ 增减 $1$，否则按正常的线段树向下递归。关键在于 $\operatorname{pushup}$：如果 $tag_u > 0$，则当前区间都被覆盖了，即为 $len_u$；当非全覆盖时，如果这里是元线段，返回 $0$，否则要将两条子线段加起来。

```cpp
void build(int u,int l,int r){
    L[u]=x[l],R[u]=x[r],len[u]=x[r]-x[l];
    if(l<r-1)build(u*2,l,(l+r)/2),build(u*2+1,(l+r)/2,r);
}
void update(int u,int l,int r,short p){
    if(l<=L[u]&&R[u]<=r)tag[u]+=p;
    else if(l<=R[u]&&L[u]<=r)update(u*2,l,r,p),update(u*2+1,l,r,p);
    if(tag[u]>0)s[u]=len[u];
    else s[u]=s[u*2]+s[u*2+1];
}
```

第二种方法：我们用普通的线段树，发现维护区间被覆盖数的最小值和被覆盖最少处的长度即可。若前者为 $0$ 则从 $len$ 中减去后者，这两个信息都具有可合并性。

扫描线的拓展：矩形并周长。

> [P1856](https://www.luogu.com.cn/problem/P1856)：给出 $n$ 个矩形的位置，求它们覆盖出的图形的总周长。

发现在扫描线上，纵边贡献的周长就是扫描线上的连续线段数乘 $2$，故线段树除了维护区间长度外，再维护有几个连续段即可。

### zkw 线段树

这是张昆玮提出的一种非递归式线段树，与普通线段树相比常数要小得多。

对一个长度为 $n$ 的序列建立的线段树，如果将 $n$ 补全至最近的 $2$ 的整次幂，那么线段树的树高不会变。而此时结点的编号、数量会变得非常有规律：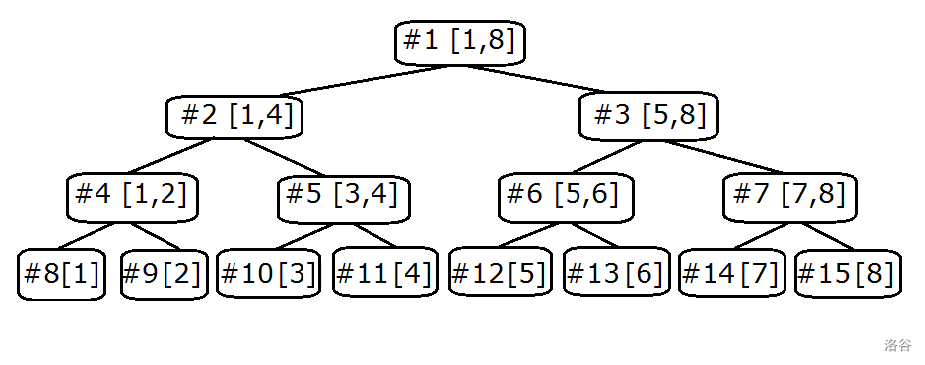

![以 $n=8$ 为例](https://cdn.luogu.com.cn/upload/image_hosting/bqlhftna.png)

发现代表 $a_i$ 的叶子编号是 $n+i-1$，于是我们就能方便地自底向上进行操作了。

当我们进行单点修改 $a_x$ 时，设 $u=n+x-1$，只需不断使 $u \leftarrow \lfloor \dfrac{u}{2} \rfloor$ 直到 $u=1$，然后循环修改所有 $u$ 结点。

区间查询也是。用两个指针维护查询区间的左右点，同样从叶子开始，逐步上跳，如果左右指针到了同一个结点就停止循环。具体怎么跳呢？

正在渲染内容...