函数与微积分简介
前置知识
高中数学必修一第一章:集合与常用逻辑用语
函数
定义
假设有两个变量 $x$,$y$ ,若对于任意 $x$ 都有唯一确定的一个 $y$ 和它对应,则称 $x$ 是自变量,$y$ 是 $x$ 的函数。$x$ 的所有使得 $y$ 有意义的取值所构成的集合叫做函数的定义域,相应地,定义域内所有的 $x$ 对应的 $y$ 所构成的集合叫做函数的值域,记作: $$y=f(x),x\in A$$ 或: $$y=f(x)$$ 其中 $x$ 是函数 $y$ 的自变量,$A$ 是函数 $y$ 的定义域。若想表达不同的函数,也可以使用其他英语和希腊字母。
通俗地讲,可以将函数理解成一种运算或操作,将一个对象转换成另一个对象。
若无特殊说明,以下一切关于函数的讨论均在其定义域内,也均讨论一元函数。
表示方法
解析式法
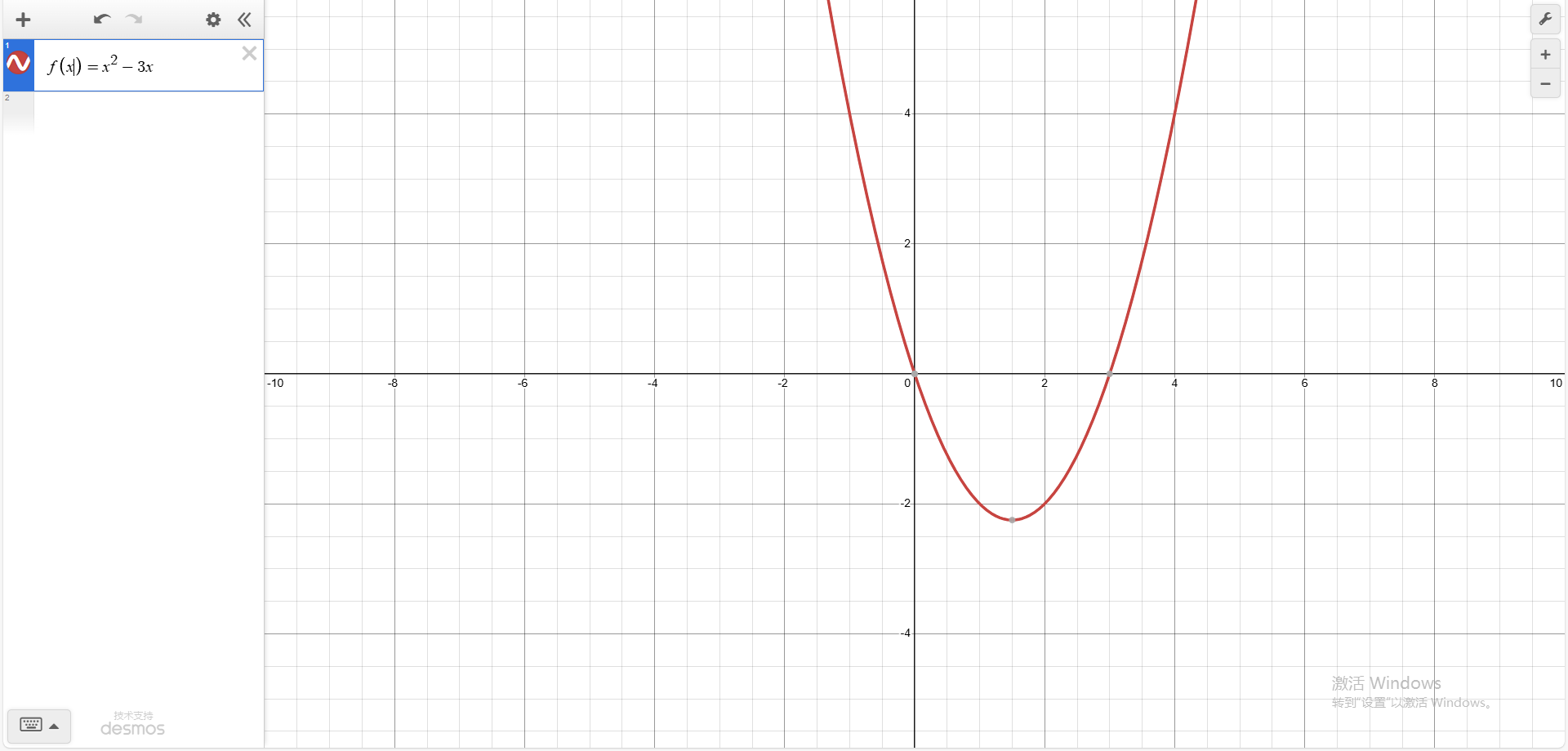
用含有数学关系的等式来表示两个变量之间的函数关系的方法叫做解析式法。这种方法的优点是能简明、准确、清楚地表示出函数与自变量之间的数量关系;缺点是求对应值时往往要经过较复杂的运算,而且在实际问题中有的函数关系不一定能用表达式表示出来。 $$示例:f(x)=x^2-3x$$
列表法
用列表的方法来表示两个变量之间函数关系的方法叫做列表法。这种方法的优点是通过表格中已知自变量的值,可以直接读出与之对应的函数值;缺点是只能列出部分对应值,难以反映函数的全貌。
$示例:$
| $x$ | $f(x)=x^2-3 x$ |
|---|---|
| $0$ | $0$ |
| $1$ | $-2$ |
| $2$ | $-2$ |
| $3$ | $0$ |
| $4$ | $4$ |
图像法
把一个函数的自变量 $x$ 与对应的函数值 $f(x)$ 分别作为点的横坐标和纵坐标,在平面直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。这种表示函数关系的方法叫做图象法。这种方法的优点是通过函数图象可以直观、形象地把函数关系表示出来;缺点是从图象观察得到的数量关系是近似的。
$示例:$
语言叙述法
使用语言文字来描述函数的关系。
本文中全程仅使用解析式法或图像法表示函数。
特性
有界性
设函数 $f(x)$ 自变量 $x$ 构成的一个区间 $A$ ,如果存在 $M_1,M_2$ ,对于所有属于区间 $A$ 里的 $x$ ,都有 $M_1\le f(x)\le M_2$ ,则称 $f(x)$ 在区间 $A$ 上有界,分别称 $M_1,M_2$ 为 $f(x)$ 在 $A$ 上的下界和上界,否则称 $f(x)$ 在区间上无界。用数学语言描述 $$\exists M_1,M_2,\forall x\in A,M_1\le f(x)\le M_2$$
单调性
设函数 $f(x)$ 自变量 $x$ 构成的一个区间 $A$ ,若对于区间 $A$ 上对于所有两点 $x_1,x_2$ ,若 $x_1<x_2$,都有$f(x_1)<f(x_2)$,则称函数 $f(x)$ 在区间 $A$ 上是单调递增的;反之,若对于区间 $A$ 上对于所有两点 $x_1,x_2$ ,若 $x_1<x_2$ ,都有 $f(x_1)>f(x_2)$ ,则称函数 $f(x)$ 在区间 $A$ 上是单调递减的。单调递增和单调递减的函数统称为单调函数。用数学语言描述 $$\forall x_1<x_2\in A,f(x_1)<f(x_2)$$ $$\forall x_1<x_2\in A,f(x_1)>f(x_2)$$
奇偶性
设一函数 $f(x)$ ,若对于任何 $x$ 满足 $f(x)=-f(-x)$ ,则称函数 $f(x)$ 为奇函数。相应地,若对于任何 $x$ 满足 $f(x)=f(-x)$ ,则称函数 $f(x)$ 为偶函数。用数学语言描述 $$\forall x,f(x)=-f(-x)$$ $$\forall x,f(x)=f(-x)$$
周期性
设一函数 $f(x)$ ,若存在一个数 $T$ ,满足对于任何 $x$ , $f(x)=f(x+T)$ ,则称函数 $f(x)$ 为周期函数。最小的满足上述条件的正数 $T$ 称为 $f(x)$ 的最小正周期。用数学语言描述 $$\exists T>0,\forall x,f(x)=f(x+T)$$
连续性
连续性严谨的定义需要用到极限,这里给出不严谨但通俗易懂的定义:设一函数 $f(x)$ ,若其图像能一笔画成,则称 $f(x)$ 为连续函数,反之则 $f(x)$ 不是连续函数。
凹凸性
设函数 $f(x)$ 在区间 $A$ 上连续,若 $$\forall x\ne y,f(\alpha x+(1-\alpha y))\ge \alpha f(x)+(1-\alpha)f(y)$$ $$\forall x\ne y,f(\alpha x+(1-\alpha y))>\alpha f(x)+(1-\alpha)f(y)$$ 则称 $f(x)$ 为凹函数。其中若满足第二个不等式,则称 $f(x)$ 为严格凹函数。同理,若 $$\forall x\ne y,f(\alpha x+(1-\alpha y))\le \alpha f(x)+(1-\alpha)f(y)$$ $$\forall x\ne y,f(\alpha x+(1-\alpha y))<\alpha f(x)+(1-\alpha)f(y)$$ 则称 $f(x)$ 为凸函数。其中若满足第二个不等式,则称 $f(x)$ 为严格凸函数。
复合函数
设函数 $f(u)$ 的定义域为 $A$ ,函数 $u=g(x)$ 在 $B$ 上有定义($B$ 是构成复合函数的定义域,它可以是 $u=g(x)$ 定义域的一个非空子集), 且 $g(x)$ 的值域 $\subset A$ ,则函数 $f(g(x))$ 称为由函数 $u=g(x)$ 和函数 $f(u)$ 构成的复合函数,它的定义域为 $A$ ,变量 $u$ 称为中间变量。
反函数
函数可以理解为从定义域映射到值域的过程。若有一函数 $f(x)$ 的映射关系为双射,则同样可以从 $f(x)$ 的值域和定义域间建立一个双射关系,这个映射的过程便是 $f(x)$ 的反函数,记作 $f^{-1}(x)$ 或 $x=f^{-1}(y)$。
分段函数
在自变量的不同变化范围内,对应法则用不同解析式子来表示的一个函数,称为分段函数。分段函数的定义域是各段定义域的并集。
隐函数
若一等式是左边只含 $y$ ,右边只含 $x$ 的算式,则称用这种方法表示的函数是显函数。若 $x$ 与 $y$ 的关系是有方程 $f(x,y)=0$ 确定的,则称 $y$ 是 $x$ 的隐函数。
参数方程
若一函数中的 $x$ , $y$ 不是直接关系的,而是由一中间变量产生关系,则称此中间变量为参数。由参数联系起来的函数关系叫做参数方程。
初等函数
由以下几种基本初等函数经过有限次的四则运算构成的复合函数叫初等函数。
- $\displaystyle f(x)=a$
- $\displaystyle f(x)=x^a(a\in \mathbb{R})$
- $\displaystyle f(x)=a^x(a>0\wedge a\ne1)$
- $f(x)=\log_ax,f(x)=\lg x,f(x)=\ln x(a\ne 1)$
- $f(x)=\sin x,f(x)=\cos x,f(x)=\tan x,f(x)=\cot x,f(x)=\sec x,f(x)=\csc x$
- $f(x)=\arcsin x,f(x)=\arccos x,f(x)=\arctan x,f(x)=\mathrm{arccot} x,f(x)=\mathrm{arcsec} x,f(x)=\mathrm{arccsc} x$
例题
例1 设 $f(x)=\frac{\ln x}{\sqrt{x-5}}$ ,若使 $f(x)$ 在实数范围内有意义,求 $f(x)$ 的定义域。
::::info[解析]
逐个分析分母和分子。若使分子在实数范围内有意义,则 $x\in(0,+\infty)$ 。若使分母在实数范围内有意义,则 $x-5\ge0$ ,即 $x\in[5,+\infty) $。由于分数分母不能为 $0$ ,所以 $\sqrt{x-5}\ne 0$ ,即 $x\in \mathbb{R}\setminus\left {5 \right}$。综合起来,
$$\begin{aligned} x&\in(0,+\infty)\cap[5,+\infty)\cap(\mathbb{R}\setminus\left {5 \right})\ &=(5,+\infty) \end{aligned} $$ 所以, $f(x)$ 的定义域为 $(5,+\infty)$ 。 :::: 例2 设函数 $f(x)=e^x$ ,分析它的单调性。
::::info[解析]
依照定义下手。
$$\begin{aligned}
\forall x_1&<x_2\in\mathbb{R}\
f(x_1)&=e^{x_1},\
f(x_2)&=e^{x_2}\
&=e^{x_1+(x_2-x_1)}\
&=e^{x_1}\cdot e^{x_2-x_1}\
f(x_2)-f(x_1)&=e^{x_1}(e^{x_2-x_1}-1)\
&\because x_2>x_1\
&\therefore e^{x_2-x_1}>1\
&\because \forall\alpha\in\mathbb{R},e^\alpha>0\
&\therefore f(x_2)-f(x_1)>0\
&\Leftrightarrow f(x_2)>f(x_1)\
\end{aligned}
$$
所以, $f(x)$ 在 $\mathbb{R}$ 内单调递增。
::::
例3 求三角函数 $f(x)=\sin x$ , $g(x)=\cos x$ 的奇偶性。
极限
不严谨定义
有限处的极限
有一函数 $f(x)$ ,若自变量 $x$ 无限趋近某定值 $a$ 时(记为 $x\to a$),对应的函数值无限趋近与另外一个定值 $L$ 则我们说当 $x\to a$, 函数 $f(x)$ 的极限是 $L$。记作 $$\lim_{x\to a}f(x)=L$$
无限处的极限
有一函数 $f(x)$ ,若自变量 $x$ 无限增大时(记为 $x\to\infty$),对应的函数值无限趋近与一个定值 $L$ 则我们说当 $x\to a$, 函数 $f(x)$ 的极限是 $L$。记作: $$\lim_{x\to\infty}f(x)=L$$ 如果 $\lim_{x\to\infty}f(x)=L$ ,则该函数具有水平渐近线 $y=L$ 。
严谨定义
自变量和极限值均为有限值的极限
若对于任意正数 $\varepsilon$ ,存在正数 $\delta$ ,使得对于所有满足 $|x-a|<\delta$ 的 $x$ , $|f(x)-L|<\varepsilon$ ,则称 $\lim_{x\to a}f(x)=L$ 。用数学语言描述: $$\lim_{x\to a}f(x)=L\Leftrightarrow\forall\varepsilon>0,\exists\delta>0,\forall x(|x-a|<\delta\Rightarrow|f(x)-L|<\varepsilon)$$
自变量为无限的极限
若对于任意正数 $\varepsilon$ ,存在正数 $\delta$ ,使得对于所有满足 $x>\delta$ 的 $x$ , $|f(x)-L|<\varepsilon$ ,则称 $\lim_{x\to \infty}f(x)=L$ 。用数学语言描述: $$\lim_{x\to \infty}f(x)=L\Leftrightarrow\forall\varepsilon>0,\exists\delta>0,\forall x(x>\delta\Rightarrow|f(x)-L|<\varepsilon)$$
极限值为无限的极限
若对于任意正数 $\varepsilon$ ,存在正数 $\delta$ ,使得对于所有满足 $|x-a|<\delta$ 的 $x$ , $f(x)>\varepsilon$ ,则称 $\lim_{x\to a}f(x)=\infty$ 。用数学语言描述: $$\lim_{x\to a}f(x)=\infty\Leftrightarrow\forall\varepsilon>0,\exists\delta>0,\forall x(|x-a|<\delta\Rightarrow f(x)>\varepsilon)$$
极限存在的条件
$$\lim_{x\to a}f(x)=L$$ 的充要条件是
- $\lim_{x\to a^-}f(x)$ 存在且 $=L$ 。
- $\lim_{x\to a^+}f(x)$ 存在且亦 $=L$ 。
极限的运算法则
$$\begin{aligned} \lim(f(x)\pm g(x))&=\lim f(x)\pm\lim g(x)\ \lim(f(x)\cdot g(x))&=\lim f(x)\cdot\lim g(x)\ \lim(\frac{f(x)}{g(x)})&=\frac{\lim f(x)}{\lim g(x)}\ \end{aligned}$$
重新定义连续性
设一函数 $f(x)$ ,若称函数在 $x=a$ 点连续,则 $$\lim_{x\to a}f(x)=f(a)$$ 若 $$\forall x\Rightarrow \lim_{x\to a}f(a)=f(a)$$ 则称该函数为连续函数,否则不是连续函数。
无穷小
若 $\lim_{x\to a}f(x)=0$ 或 $\lim_{x\to\infty}f(x)=0$ ,则称 $f(x)$ 是 $x\to a$ 或 $x\to\infty$ 时的无穷小。
无穷小的比较
若 $\lim_{x\to a}\alpha=0$ 且 $\lim_{x\to a}\beta=0$ :
- 若 $\displaystyle\lim_{x\to a}\frac{\alpha}{\beta}=0$ ,则 $\alpha$ 是比 $\beta$ 较高阶的无穷小。
- 若 $\displaystyle\lim_{x\to a}\frac{\alpha}{\beta}=\infty$ ,则 $\alpha$ 是比 $\beta$ 较低阶的无穷小。
- 若 $\displaystyle\lim_{x\to a}\frac{\alpha}{\beta}=k\ne0$ ,则 $\alpha$ 是与 $\beta$ 同阶的无穷小。
- 若 $\displaystyle\lim_{x\to a}\frac{\alpha}{\beta}=1$ ,则 $\alpha$ 是与 $\beta$ 等阶的无穷小,记作: $\alpha\sim\beta$ 。
等阶无穷小的变换
若 $\alpha\sim\alpha’$ , $\beta\sim\beta’$ ,存在 $\lim\frac{\beta’}{\beta}$ ,则 $\lim\frac{\alpha}{\beta}=\lim\frac{\alpha’}{\beta’}$ 。
夹逼准则
若 $$\forall x\Rightarrow g(x)\le f(x)\le h(x)\wedge\lim g(x)=\lim h(x)=L$$ 则 $\lim f(x)=L$ 。
例题
例1 求 $\lim_{x\to 1}(2x-1)$ 。
例2 求 $\lim_{x\to 3}\frac{x-3}{x^2-9}$ 。
例3 求 $\lim_{x\to\infty}\frac{2x-1}{5x+7}$
例4 求 $\lim_{x\to\infty}\frac{2x^2-1}{5x+7}$
例5 求 $\lim_{x\to 0}\frac{\sin x}{x}$
例6 求 $\lim_{x\to 0}\frac{\tan x}{x}$
例7 求 $\lim_{x\to 0}\frac{\arcsin x}{x}$
导数
定义
设函数 $f(x)$ 在区间 $A$ 上有定义,若区间内一点 $x_0$ 有一增量 $\Delta x$ ,对应函数值 $y$ 有一增量 $\Delta y=f(x_0+\Delta x)-f(x_0)$ 则称 $$\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$ 为函数 $f(x)$ 在点 $x_0$ 处的导数。
几何意义
函数 $f(x)$ 的图像在点 $x_0$ 处切线的斜率。
导函数
若函数 $f(x)$ 的导数 $g(x)$ 仍是 $x$ 的函数,则称 $g(x)$ 是 $f(x)$ 的导函数。
导数的表示方法
导数的表示方法繁多,这里只列举常用的:
- 拉格朗日记号: $f’(x),y’$
- 拉格朗日记号: $f’_x(x,y)$ (用于明确自变量或用于多元函数)
- 莱布尼茨记号: $\frac{\mathrm{d}}{\mathrm{d}x}f(x),\frac{\mathrm{d}y}{\mathrm{d}x}$
- 莱布尼茨记号: $\frac{\partial}{\partial x}f(x,y),\frac{\partial y}{\partial x}$ (用于多元函数)
- 牛顿记号: $\dot{y}$
导数存在的条件
$\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ 存在。 若对于函数定义域的每一点都存在导数,则称该函数为可导函数。否则若函数在一点 $a$ 不存在导数,则称函数在 $a$ 点不可导。
导数与连续性的关系
函数 $f(x)$ 在 $a$ 点连续是函数在 $a$ 点可导的必要条件。而函数 $f(x)$ 在 $a$ 点可导是函数 $f(x)$ 在 $a$ 点连续的充分条件。即可导必连续,不可导不一定连续,不连续一定不可导,连续不一定可导。
导数的运算法则
$$\begin{aligned} (f(x)\pm g(x))‘&=f’(x)\pm g’(x)\ (f(x)g(x))‘&=f’(x)g(x)+f(x)g’(x)\ \frac{f(x)}{g(x)}&=\frac{f’(x)g(x)-f(x)g’(x)}{(g(x))^2}\ f(g(x))&=f’(u)\cdot g’(x)(u=g(x))\ f’(x)&=\frac{1}{f^{-1}(y)}\
\end{aligned}$$
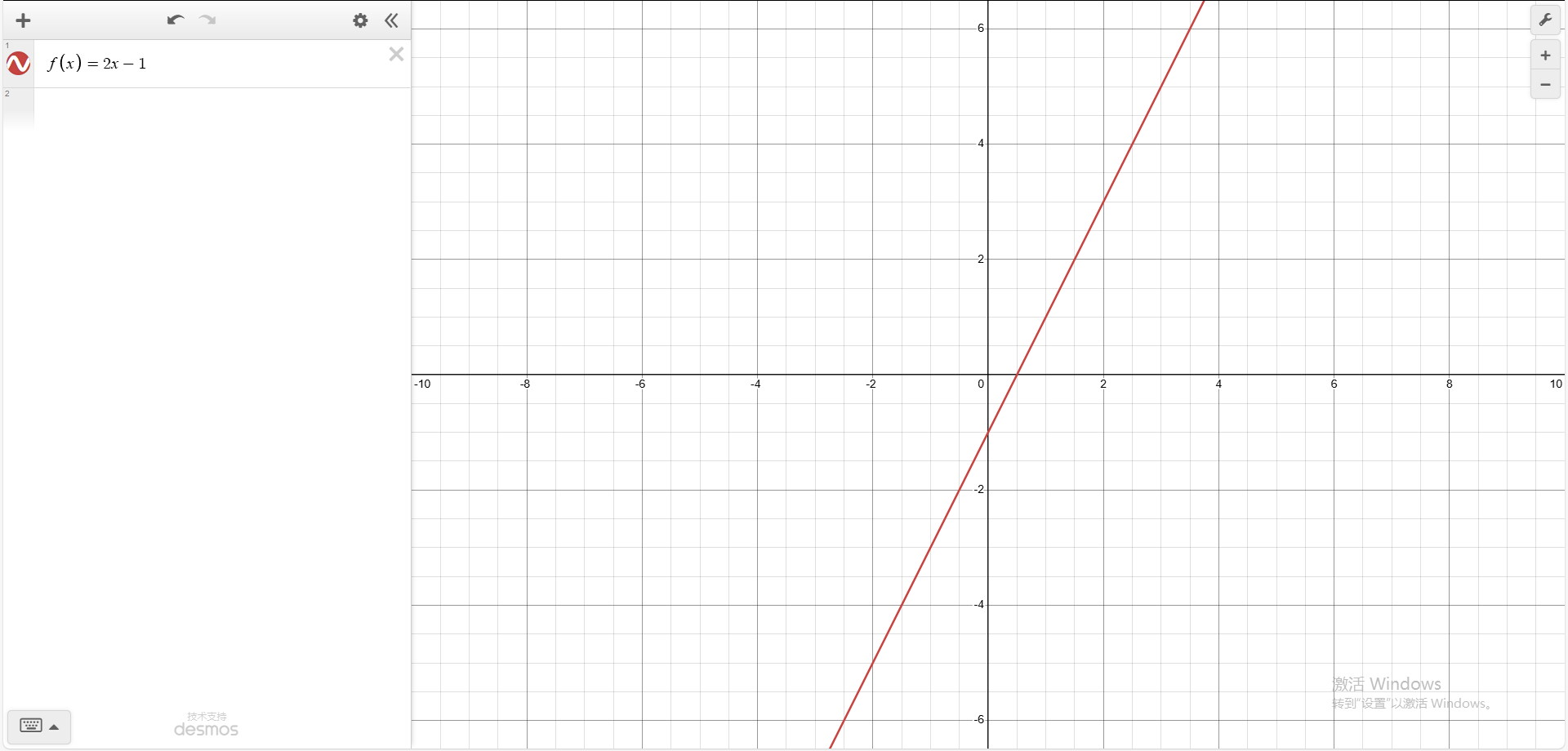 易看出,此函数在它的定义域各处连续,所以,对于任意的 $a$ ,满足 $\lim_{x\to a}f(x)=f(a)$ ,所以
$$\lim_{x\to 1}(2x-1)=2\times1-1=1$$
易看出,此函数在它的定义域各处连续,所以,对于任意的 $a$ ,满足 $\lim_{x\to a}f(x)=f(a)$ ,所以
$$\lim_{x\to 1}(2x-1)=2\times1-1=1$$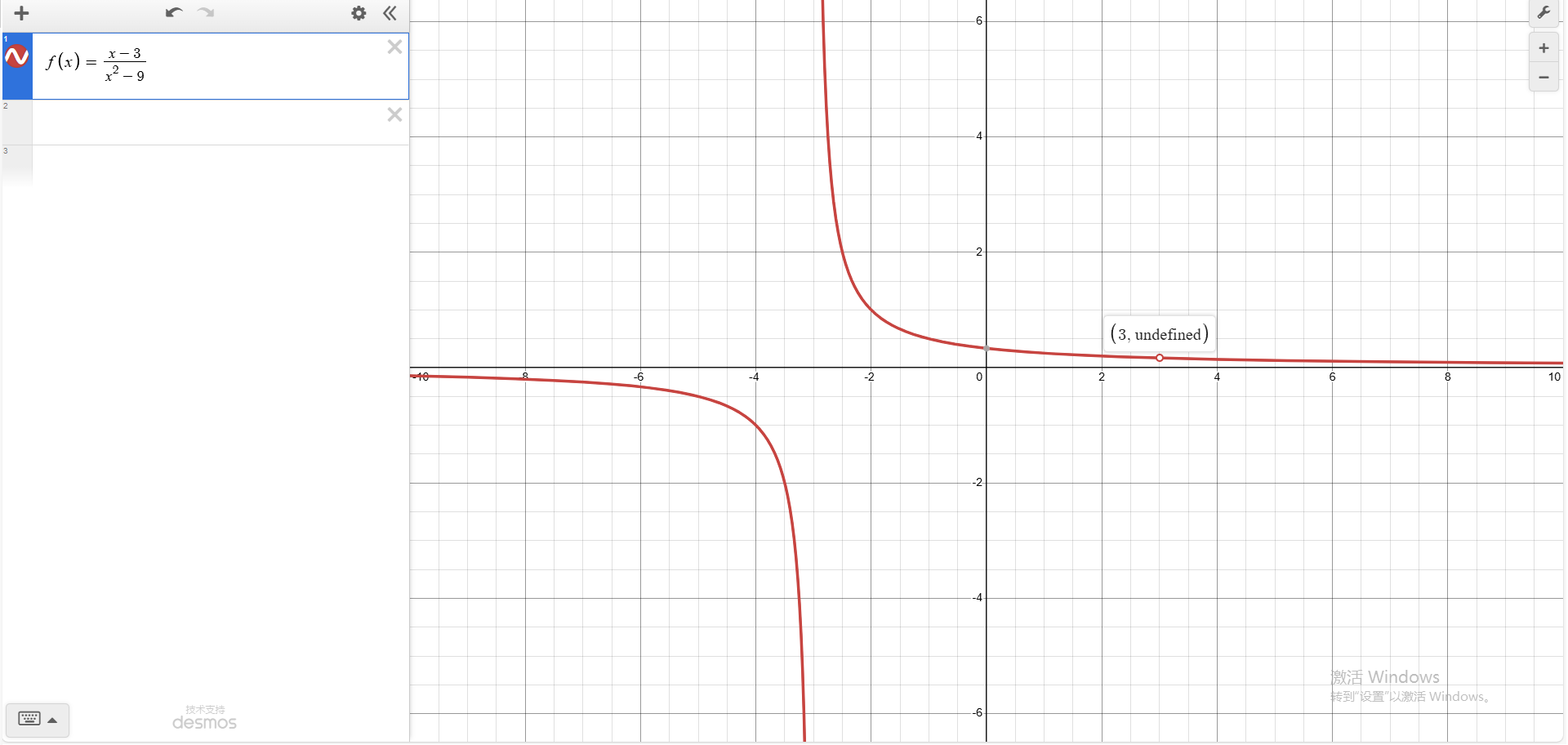 注意到,函数在 $x=3$ 处并不连续,所以无法代入求极限。但是可以对原函数进行一些变形再求极限。注意到 $9=3^2$ ,根据平法差公式 $a^2-b^2=(a+b)(a-b)$ ,我们可以对分子经行因式分解:
$$\begin{aligned}
f(x)&=\frac{x-3}{x^2-9}\
&=\frac{x-3}{x^2-3^2}\
&=\frac{x-3}{(x+3)(x-3)}\
&=\frac{1}{x+3}\
\end{aligned}$$
注意到,这时的函数在 $x=3$ 处连续,我们便使用函数的连续性求得:
$$\lim_{x\to 3}\frac{1}{x+3}=\frac{1}{3+3}=\frac{1}{6}$$
这更加体现了,很多极限题是无法直接代入的,得对函数进行变形或借助工具才能求解。也说明了极限值不是函数值,极限是不能直接代入的。
注意到,函数在 $x=3$ 处并不连续,所以无法代入求极限。但是可以对原函数进行一些变形再求极限。注意到 $9=3^2$ ,根据平法差公式 $a^2-b^2=(a+b)(a-b)$ ,我们可以对分子经行因式分解:
$$\begin{aligned}
f(x)&=\frac{x-3}{x^2-9}\
&=\frac{x-3}{x^2-3^2}\
&=\frac{x-3}{(x+3)(x-3)}\
&=\frac{1}{x+3}\
\end{aligned}$$
注意到,这时的函数在 $x=3$ 处连续,我们便使用函数的连续性求得:
$$\lim_{x\to 3}\frac{1}{x+3}=\frac{1}{3+3}=\frac{1}{6}$$
这更加体现了,很多极限题是无法直接代入的,得对函数进行变形或借助工具才能求解。也说明了极限值不是函数值,极限是不能直接代入的。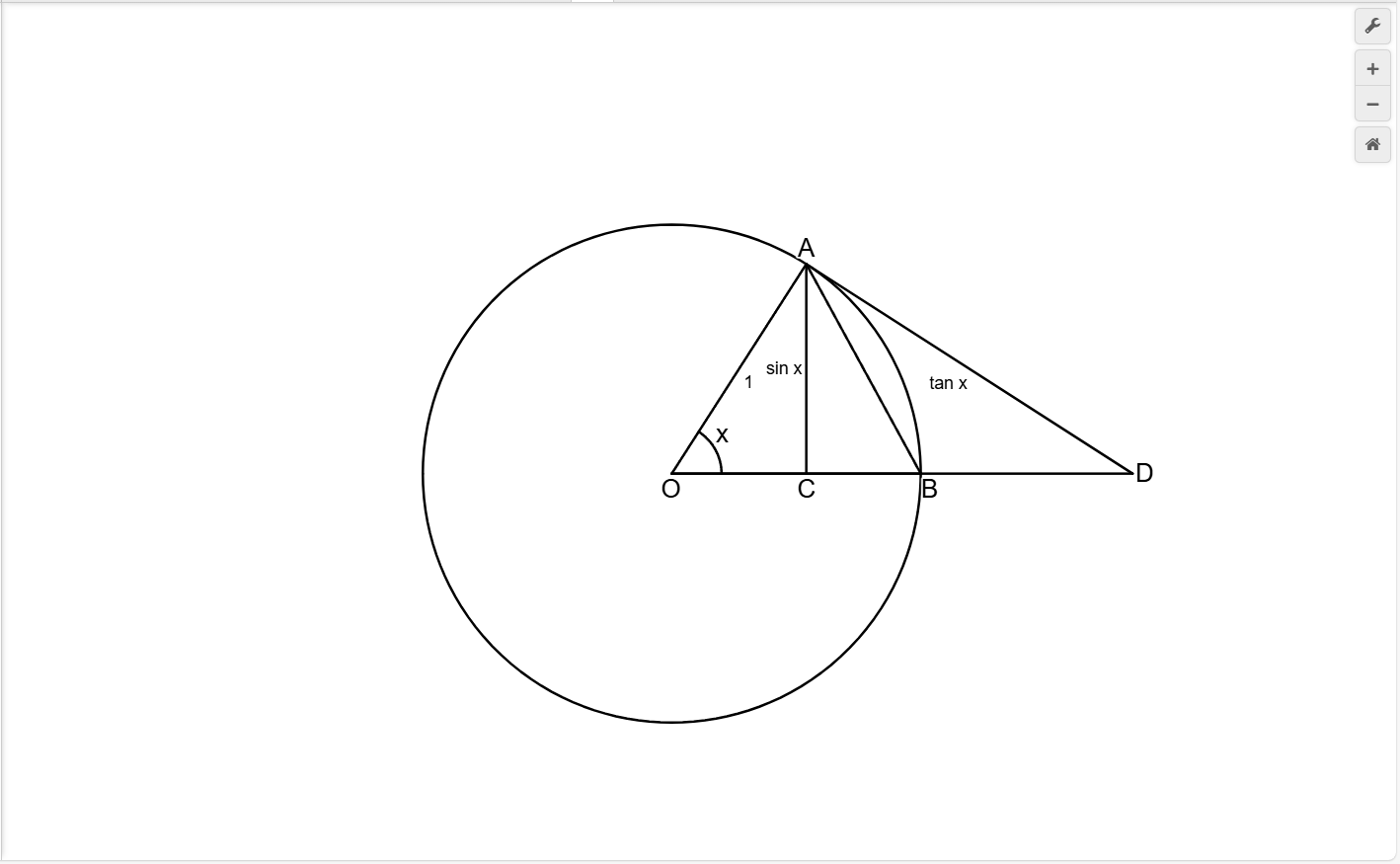 如图,作一单位圆 $\odot O$ , $AD$ 切 $\odot O$ 与 $A$ , $AC\bot OB$ 。当 $x\in(0,\frac{\pi}{2})$ , $x=弧AB$ , $\sin x=AC$ , $\tan x=AD$ 。
$$\begin{aligned}
&\because\forall x\in(0,\frac{\pi}{2}),S_{\triangle AOB}<S_{扇形AOB}<S_{\triangle AOD}\
&\therefore \frac{\sin x}{2}<\frac{x}{2}<\frac{\tan x}{2}\
&\sin x<x<\tan x\
&\frac{\sin x}{\sin x}<\frac{x}{\sin x}<\frac{\tan x}{\sin x}\
&1<\frac{x}{\sin x}<\frac{1}{\cos x}\
&1>\frac{\sin x}{x}>\cos x\
&\because \lim_{x\to 0}1=1,\lim_{x\to 0}\cos x=1
\end{aligned}$$
套用夹逼准则有
$$\lim_{x\to 0}\frac{\sin x}{x}=1$$
其实这道题还可以用洛必达法则快速求出,具体可以找下一节:导数。
如图,作一单位圆 $\odot O$ , $AD$ 切 $\odot O$ 与 $A$ , $AC\bot OB$ 。当 $x\in(0,\frac{\pi}{2})$ , $x=弧AB$ , $\sin x=AC$ , $\tan x=AD$ 。
$$\begin{aligned}
&\because\forall x\in(0,\frac{\pi}{2}),S_{\triangle AOB}<S_{扇形AOB}<S_{\triangle AOD}\
&\therefore \frac{\sin x}{2}<\frac{x}{2}<\frac{\tan x}{2}\
&\sin x<x<\tan x\
&\frac{\sin x}{\sin x}<\frac{x}{\sin x}<\frac{\tan x}{\sin x}\
&1<\frac{x}{\sin x}<\frac{1}{\cos x}\
&1>\frac{\sin x}{x}>\cos x\
&\because \lim_{x\to 0}1=1,\lim_{x\to 0}\cos x=1
\end{aligned}$$
套用夹逼准则有
$$\lim_{x\to 0}\frac{\sin x}{x}=1$$
其实这道题还可以用洛必达法则快速求出,具体可以找下一节:导数。