往期题目精讲

Positions in Permutations

给定 $n,m$，求所有 $1\sim n$ 的排列 $p$ 的数量，满足 $$ \sum_{i=1}^n[|p_i-i|=1]=m $$ 对 $P=10^9+7$ 取模。

$1\le n\le 1000$，$0\le m\le n$。

考虑恰好有 $m$ 个 $i$ 满足 $|p_i-i|=1$ 不好做，不妨令 $f(S)$ 表示至少所有 $i\in S$ 的 $i$ 满足 $|p_i-i|=1$，其余不在 $S$ 中的 $i$ 满不满足无所谓的 $p$ 的数量；再令 $g(S)$ 表示 $|p_i-i|=1$ 当且仅当 $i\in S$ 的 $p$ 的数量；那么答案就是 $\sum_{|S|=m}g(S)$，根据定义 $f(S)=\sum_{S\subseteq T}g(T)$，子集和变换即得 $g(S)=\sum_{S\subseteq T}(-1)^{|T|-|S|}f(T)$。 $$ \begin{aligned}\sum_{|S|=m}g(S)&=\sum_{|S|=m}\sum_{S\subseteq T}(-1)^{|T|-|S|}f(T)\&=\sum_{T}\binom{|T|}{m}(-1)^{|T|-m}f(T)\end{aligned} $$ 考虑 $f(T)$ 相当于先给满足 $i\in T$ 的 $p_i$ 分配值，然后给 $i\not\in T$ 的 $p_i$ 分配；后一步的方案数总是 $(n-|T|)!$，因此我们令 $h(T)$ 表示给 $i\in T$ 分配 $p_i$ 的方案数，那么 $f(T)=(n-|T|)!h(T)$。观察推出的式子，发现有很多只和 $|T|$ 有关的项，我们考虑整理到一起： $$ \sum_{i=m}^n\binom{i}{m}(-1)^{i-m}(n-i)!\sum_{|S|=i}h(S) $$ 现在问题变成求解 $\sum_{|S|=i}h(S)$。注意到无论 $S$ 长什么样，如果 $i\in S$ 那么 $p_i$ 只能取 $i+1$ 或 $i-1$，也就是说这个位置的取值只会影响到之前 $O(1)$ 个位置。考虑 dp，设 $f(i,j,0/1,0/1)$ 表示当前考虑到第 $i$ 个元素，当前 $|S|=j$，是否有元素选了 $i$，是否有元素选了 $i+1$ 的答案。那么考虑 $i$ 要不要选、选的话选 $i-1$ 还是 $i+1$ 进行转移即可。答案即为 $\sum_{|S|=i}h(S)=\sum_{x,y\in{0,1}}f(n,i,x,y)$。

树分治进阶

边分治

Problem 0

给定一棵 $n$ 个点的树，边有非负边权；一开始有 $n$ 个集合，第 $i$ 个集合只有 $\set i$ 一个点；$n$ 次操作，每次指定两个集合 $S,T$，询问分别在 $S,T$ 中选择一个点 $u,v$，$dis(u,v)$ 的最大值，然后合并集合 $S,T$。

$1\le n\le 10^6$。

那如果最远点对有多个会不会影响答案呢？要不要都维护出来？手摸了好久发现，要么只有一个最远点对，要么此时边权均相同，也就是维护一对最远点对即可。

边分治，顾名思义每次取一条边，将树分成两个部分进行分治。有一个结论：当每个节点的度数都 $\le d$ 时，总是存在一条边使得两侧的子树大小均不超过 $n(d-1)/d$。也就是当 $d$ 比较小的时候，边分治复杂度比较优。为了使 $d$ 变小考虑把一个孩子很多的 $u$ 进行改造。对于 $u$ 的若干个孩子 $v_1,v_2,\cdots,v_k$，几种改造方法：

• 给每个孩子建一个虚点 $v_1’,\cdots,v_k’$，并且连 $(v_i,v_i’)$；然后把相邻的虚点连起来，最后连 $(u,v_1’)$。
• （自己知道的一种）类似于线段树，每次分成左右两部分，建一个虚点，连向 $u$，然后递归。

这样可以保证每个点的度数不会太大，但是缺点是可能会使点上的一些信息丢失了（比如说可能无法表达出原树 $\operatorname{lca}$ 信息），不过边的信息还算完整。这样每轮树分治我们就会得到两棵子树，就可以做一些 $O(\text{子树大小})$ 的操作了。总时间复杂度 $O(n\log n)$。

Problem 1

给定两棵 $n$ 个点的带边权树，求一对点 $(u,v)$ 满足它们在两颗树上的距离和最大。

$1\le n\le 10^6$，边权非负。

考虑在第一棵树上做边分治，这样问题转化成： $$ d_u+d_v+w+\operatorname{dis}_2(u,v) $$

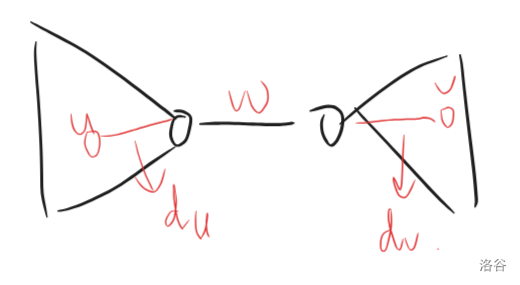
并且要求 $u,v$ 两个点异色。这相当于在第二棵树中给每个点赋了一个点权 $d_u$，可以证明在有点权后 Problem 0 的结论仍然是正确的，也就是我们可以把当前第一棵树中处理的部分在第二棵树上建一颗虚树，虚树中每个节点维护子树中两种颜色的最远点对。

Problem 2

给定两棵 $n$ 个点的带边权树，求一对点 $(u,v)$ 满足它们在两棵树上的距离和最大。

$1\le n\le 10^6$，边权可能为负。

把第二棵树虚树上合并最远点对改成树形 dp 即可。

混沌邪恶 · Problem 3

给定三棵 $n$ 个点的带边权树，求一对点 $(u,v)$ 满足它们在三棵树上距离和最大。

$1\le 10^5$，边权非负。

做法一

设这三棵树分别为 $T_0,T_1,T_2$，我们在 $T_0$ 上做边分治，得到当前处理的点集 $S_0$，在 $T_1$ 上建出包含 $S_0$ 的虚树 $T_1’$；继续在 $T_1’$ 上做边分治，得到当前处理的点集 $S_1$，在 $T_2$ 上建出包含 $S_1$ 的虚树 $T_2’$，在 $T_2’$ 上做树形 dp 统计答案。在使用 $O(1)$ 查询 $\operatorname{lca}$ 和归并排序后复杂度为 $O(n\log^2n)$。

卡了 $\displaystyle\Huge72$ 小时常未能通过 uoj 最后两个测试点。

做法二

注意到边权非负，那么可以使用 Problem 1 的结论，仅对 $T_0$ 进行边分治，式子变成 $$ d_u+d_v+w+\operatorname{dis}_1(u,v)+\operatorname{dis}2(u,v) $$ 仍然建出 $T_1$ 的虚树 $T_1’$，在 $T_1’$ 上进行树形 dp，式子变成 $$ d_u+d_v+w+dep_u+dep_v-2dep{\operatorname{lca}(u,v)}+dis_2(u,v) $$ 其中 $dep_u$ 表示 $u$ 在 $T_1’$ 中到根节点的路径和。可以发现这相当于在 $T_2$ 上做带点权的最远点对，直接按照 Problem 1 的做法做即可。最终时间复杂度 $O(n\log n)$，加上前面的卡常跑得飞快。

点分治 · 合并优化

点分治相较于边分治，需要合并多个子树而不是只需要合并两个。通常维护贡献的方法是先放在一起求，再删掉同一颗子树的贡献；也可以一个个考虑子树，合并进已有答案里。

**点分治的合并优化：**每次我们在没合并的所有子树中挑两个子树大小最小的进行合并，统计完贡献之后合并成一棵树。可以证明这样优化后点分治的总复杂度仍然为 $O(n\log n)$，并且每次合并都有 $O(\text{子树大小})$ 的时间处理。由于点分治不需要对树进行重构，因此合并优化后的点分治差不多严格强于边分治。不过边分治方便分析这一点还是可以的。

有根点分治 / 边分治

Problem 4

给定两棵 $n$ 个点的有根树 $T_0,T_1$，边有可能为负的边权；求所有点对 $(u,v)$ 中 $$ dep_u+dep_v-dep_{\operatorname{lca}(u,v)}-dep’_{\operatorname{lca(u,v)}} $$ 的最大值。

$n\le 10^5$。

注意到此时 $\operatorname{lca}(u,v)$ 需要依照原树的根进行计算。继续考虑边分治（把所有挂在 $u$ 下面的虚点的深度设为 $dep_u$ 就可以解决 $\operatorname{lca}$ 在虚点上的问题），假设分治到 $(u,v)$ 这条边，因为要考虑原树的根，因此令 $v$ 是 $u$ 的父亲。

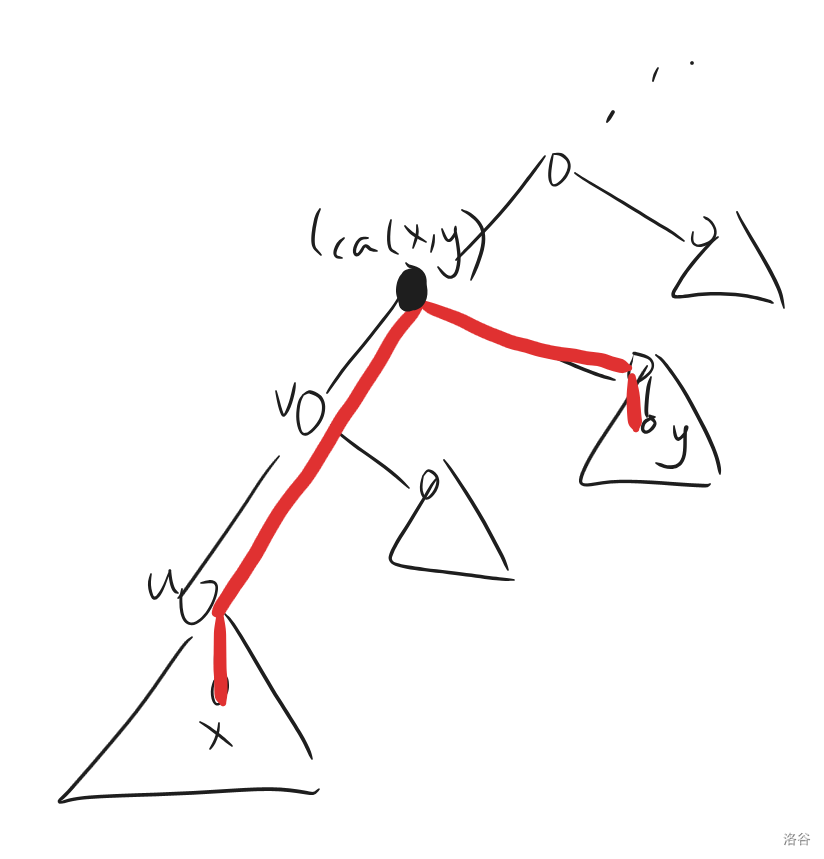
现在考虑一对路径经过 $(u,v)$ 的点对 $(x,y)$，假设 $x$ 在 $u$ 的子树里，那么此时的 $\operatorname{lca}(x,y)$ 就是图中的黑色点；可以发现每层的边分治中，这个黑色点的位置只和 $y$ 的位置有关，因此我们可以把减去的 $\operatorname{lca}$ 的深度算在 $y$ 的点权上，也即令 $y$ 的点权 $val_y=dep_y-dep_{y’}$；而 $x$ 的点权 $val_x=dep_x$。这样题目求的就是 $$ val_x+val_y-dep’_{\operatorname{lca(x,y)}} $$ 的最大值，直接在第二棵树上建出虚树并进行树形 dp 即可。最优复杂度 $O(n\log n)$。

other problems

汽水

题解链接

配对树

给定一棵 $n$ 个点的带边权的树和一个长度为 $m$ 的值域在 $[1,n]$ 序列 $a$；对于一个长度为偶数的区间 $[L,R]$，满足 $1\le L\le R\le m$，你需要将 $a$ 中 $[L,R]$ 的部分两两分组，将 $i,j$ 分为一组的代价是 $a_i,a_j$ 在树上的路径边权和。求对所有长度为偶数的区间分别进行分组的最小代价的和。对 $998244353$ 取模。

$1\le n,m\le 10^5$，$w\le 10^9$。

考虑对于一组关键点 $p_1,p_2,\cdots,p_k$ 怎么分组是最优的。

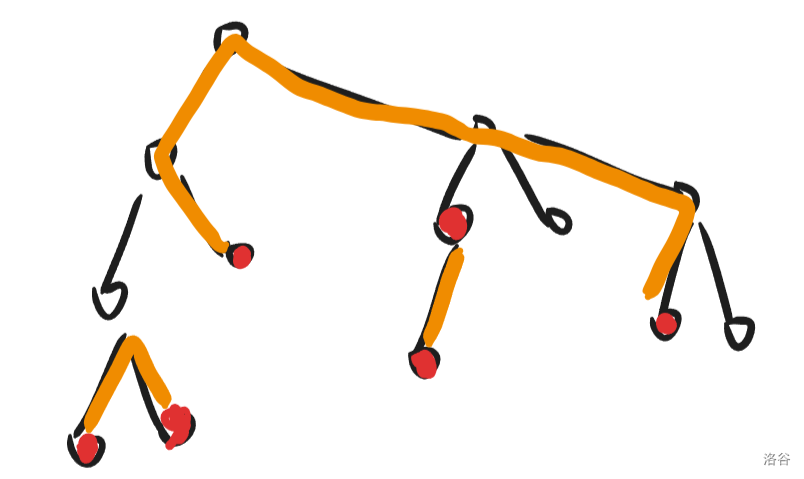
图中红色的点即为 $p_i$，橙色的路径代表一组分组。可以发现，对于某个点 $u$，如果在它的子树里有偶数个关键点，那么显然子树里的关键点只和子树里的关键点匹配是最优的；否则会剩一个关键点留着和 $u$ 子树外的一个关键点匹配。这就说明，对于一组固定的关键点，一条边 $(u,v)$（假设 $u$ 的深度大于 $v$）至多只会出现在代价中一次，且出现一次当且仅当 $u$ 的子树中有奇数个关键点。

那就来考虑一条边 $(u,v)$ 会在多少个偶区间中作为代价出现，则它对答案的贡献就是边权乘上出现次数。设 $u$ 子树中的节点有 $p_1,p_2,\cdots,p_k$，将它们在 $a$ 中所有出现的位置染色，那么相当于数有多少个区间 $[l,r]$，满足 $2\mid (r-l+1)$ 且区间中有奇数个位置被染色。设 $[1,i]$ 中共有 $s_i$ 个位置被染色，则对于一个 $j<i$，满足 $2\mid (i-j)$ 且 $s_j\not\equiv s_i\pmod 2$，那么 $[j+1,i]$ 就是一个合法的区间。

考虑用 dp 表示这么一件事情，设 $f(i,x\in\set {0,1},y\in\set{0,1})$ 表示所有 $j\in [0,i-1]$ 中满足 $j\bmod 2=x$、$s_j\bmod 2=y$ 的 $j$ 的个数；转移直接考虑 $i$ 的情况即可，则答案就是 $$ f(n,0,0)\times f(n,0,1)+f(n,1,0)\times f(n,1,1) $$ 对于每个点 $u$ 我们都需要维护这个一个 dp 数组，而有祖孙关系的点对，其染色情况是子集的关系，因此可以考虑用线段树维护这个 dp 数组，然后使用线段树合并。时间复杂度 $O(m\log m)$。