主页
搜索
最近更新
数据统计
申请密钥
系统公告
1
/
1
请查看完所有公告
浅谈平衡树
最后更新于 2025-07-31 11:22:03
作者
stripe_python
分类
算法·理论
复制 Markdown
查看原文
删除文章
更新内容
# 前言 教练的任务。本来想写线段树来着,被人占了,那就写平衡树罢。 # BST BST,全称 Binary Search Tree,即二叉搜索树,其定义为: 1. 空树是 BST; 2. 左子树的权值小于根节点; 3. 右子树的权值大于根节点; 4. 左右子树均为 BST。 可以发现 BST 具有一些良好性质,比如中序遍历有序。 ## 操作 ### 定义节点 ```cpp template <class T> class BinarySearchTreeNode { public: T val; BinarySearchTreeNode<T> *left, *right; long cnt, size; BinarySearchTreeNode() : val(T()), left(nullptr), right(nullptr), cnt(1), size(1) {} BinarySearchTreeNode(const T& v) : val(v), left(nullptr), right(nullptr), cnt(1), size(1) {} BinarySearchTreeNode<T>* pushup() { size = cnt + (left ? left->size : 0) + (right ? right->size : 0); return this; } }; ``` 通过指针来存左右节点。类似权值线段树,要维护每个节点的 `size`。这里我们维护的是可重集,要维护 `cnt` 表示该点上权值出现的次数。 ### 插入节点 ```cpp void insert(node*& cur, const T& val) { if (!cur) { cur = new node(val); return; } if (val == cur->val) { cur->cnt++, cur->pushup(); return; } if (cmp(val, cur->val)) insert(cur->left, val); else insert(cur->right, val); cur->pushup(); } ``` 首先根据 BST 的结构,你可以把权值与当前点权值比较,小于走左子树,大于走右子树。当找到该权值或者到了叶子节点就新建一个节点。 ### 删除节点 ```cpp static node* get_min(node* cur) { // 找 cur 子树内最小值 node *x = cur; while (x && x->left) x = x->left; return x; } bool remove_node(node*& cur) { if (!cur) return false; if (cur->cnt > 1) { // Case 1 cur->cnt--, cur->pushup(); return true; } if (cur->left && cur->right) { // Case 2 node* replace = this->get_min(cur->right); cur->cnt = replace->cnt, cur->val = replace->val; // 以 replace 上提代替 cur replace->cnt = 1; remove(cur->right, replace->val); // 将 replace 从右子树中删去 } else { // Case 3 & 4 cur = cur->left ? cur->left : cur->right; } if (cur) cur->pushup(); // 注意防空指针 return true; } bool remove(node*& cur, const T& val) { if (!cur) return false; if (val == cur->val) return remove_node(cur); bool res; if (cmp(val, cur->val)) res = remove(cur->left, val); else res = remove(cur->right, val); if (cur) cur->pushup(); return res; } ``` BST 的删除比较复杂。分类讨论一波: - 若 `cnt` 大于 $1$,直接减少 `cnt` 即可; - 若 `cnt` 等于 $1$: - - 若 `cur` 为叶子节点,直接删除; - 若 `cur` 只有一个儿子,用这个儿子替代之; - 若 `cur` 有两个儿子,用它右子树最小值上提来代替。根据 BST 结构,从右子树开始走左链即可。 ### 查询排名 先定义一波排名: > $x$ 的排名为当前数组内小于 $x$ 的数的个数 $+1$。 ```cpp int rank(node* cur, const T& val) const { if (!cur) return 1; int left_size = cur->left ? cur->left->size : 0; if (val == cur->val) return left_size + 1; if (cmp(val, cur->val)) return rank(cur->left, val); return rank(cur->right, val) + left_size + cur->cnt; } ``` 写过权值线段树应该好理解。首先先寻找这个元素。如果向左跳就没有贡献,如果向右跳,当前节点和左子树内的全部元素都小于 $x$,答案加上左子树大小加上当前 `cnt`。找到节点以后,左儿子的元素也小于它,加上左子树大小。 ### 查询排名为 $k$ 的数 ```cpp T kth(node* cur, int k) const { if (!cur) return -1; // k 不在范围内,返回无效值 int left_size = cur->left ? cur->left->size : 0; if (left_size >= k) return kth(cur->left, k); if (left_size < k - cur->cnt) return kth(cur->right, k - left_size - cur->cnt); return cur->val; } ``` 可以看作是 `rank` 的逆操作。 记左子树大小为 $s$,分类讨论: - 若 $k \le s$,这个数就在左子树里; - 若 $s \in [k-cnt,k-1]$,那么这个点就是根节点; - 若 $k>s$,这个数在右子树,注意递归时减去 $s+cnt$。 ## 复杂度 普通平衡树这玩意,说白了是给 `std::multiset` 加了两个排名操作。 我们来分析一下 BST 的复杂度。由于每次操作都要找到节点,时间复杂度与深度成正比,即 $O(h)$。一般地,在随机数据下,$h$ 期望为 $O(\log n)$ 级别。而在构造数据下 $h$ 可退化为 $O(n)$。 比如顺序插入一组数,手玩一下,你会发现 BST 成链表了。 # 平衡树 不过我们发现 BST 和二叉堆一样,都是弱定义,可以有多种合法结构,如果我们能通过一些操作将树高控制在 $O(\log n)$,平衡树就变成了 $O(q \log n)$ 的数据结构。 ## AVL AVL 树是工程中常用的平衡树。它对平衡的定义比较强。具体来说,我们在每个节点维护一个平衡因子,它在数值上等于右子树高度减去左子树高度,我们要保证其绝对值不大于 $1$。这样树高就是 $O(\log n)$ 了。 > 证明:设 $f_h$ 为高为 $h$ 的 AVL 树所包含的最少节点数,则 $f_h=f_{h-1}+f_{h-2}+1$,因为左右子树最多差开 $1$。可以发现 $f_h+1$ 是斐波那契数列。而斐波那契数列是指数增长的,所以树高是 $\log$ 级别。 ### 维护平衡 显然破坏平衡的操作就只有插入 / 删除这样改变形态的操作。 我们引入左旋右旋操作来维护平衡。先举一个左旋例子: 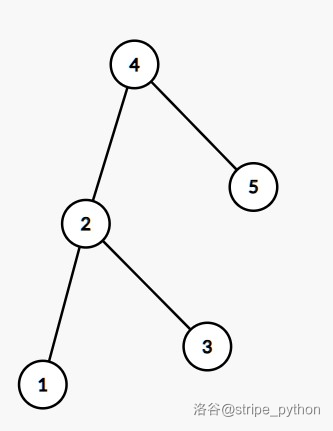 这棵 BST 可以调整为: 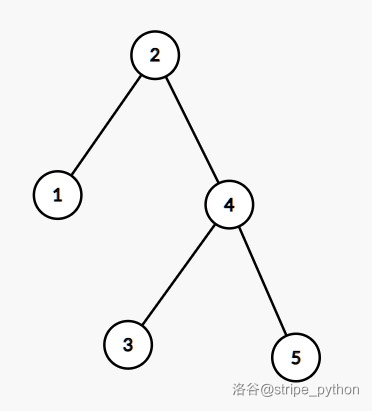 对于节点 $4$,进行一次右旋,将其左儿子 $2$ 上提为根,左儿子的右儿子 $3$ 成为 $4$ 的左儿子。左旋即为此逆操作,代码如下: ```cpp static node* left_rotate(node* p) { node *q = p->left; p->left = q->right, q->right = p, p->pushup(); return q->pushup(); } static node* right_rotate(node* p) { node *q = p->right; p->right = q->left, q->left = p, p->pushup(); return q->pushup(); } ``` 分类讨论破坏平衡的情况: 1. LL 型(左孩子的左孩子过深),如图: 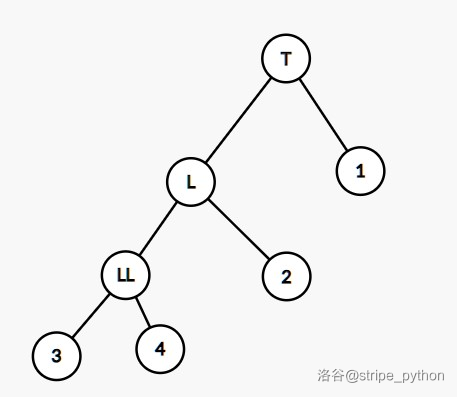 解法:右旋节点 $T$。这样 $L$ 得以上提,平衡因子从 $-2$ 变为 $-1$。 2. LR 型(左孩子的右孩子过深),如图: 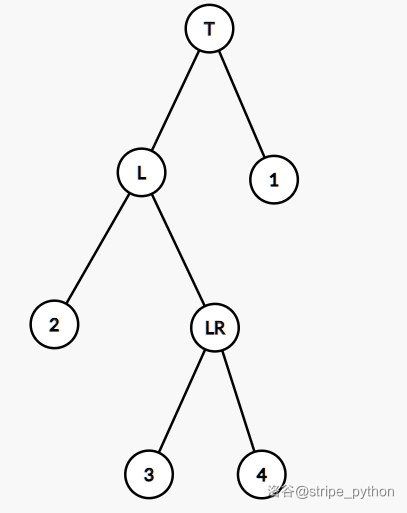 解法:左旋节点 $L$,这样就成为了 LL 型,然后右旋节点 $T$ 即可。 还有 RR 型、RL 型两种情况,与上述情况对称。 ### 操作 我们改改插入操作: ```cpp static node* left_right_rotate(node* p) { p->left = right_rotate(p->left); return left_rotate(p); } static node* right_left_rotate(node* p) { p->right = left_rotate(p->right); return right_rotate(p); } if (cmp(val, cur->val)) { insert(cur->left, val), cur->pushup(); if (get_high(cur->left) - get_high(cur->right) >= 2) { // 失衡,RR / RL 型 cur = cmp(val, cur->left->val) ? left_rotate(cur) : left_right_rotate(cur); } } else { insert(cur->right, val), cur->pushup(); if (get_high(cur->right) - get_high(cur->left) >= 2) { // 失衡,LL / LR 型 cur = cmp(val, cur->right->val) ? right_left_rotate(cur) : right_rotate(cur); } } ``` 还是容易理解的。但是删除和原 BST 不太一样。 ```cpp bool remove_node(node*& cur) { if (!cur) return false; if (cur->cnt > 1) { cur->cnt--, cur->pushup(); return true; } if (cur->left && cur->right) { node* replace = this->get_min(cur->right); cur->cnt = replace->cnt, cur->val = replace->val; replace->cnt = 1; remove(cur->right, replace->val), cur->pushup(); // 由于上提的是右子树最小值,只会导致 RR / RL 型失衡(思考一下为什么) if (get_high(cur->left) - get_high(cur->right) >= 2) { // 失衡,RR / RL 型 cur = (get_high(cur->left->left) >= get_high(cur->left->right)) ? left_rotate(cur) : left_right_rotate(cur); } } else { cur = cur->left ? cur->left : cur->right; } if (cur) cur->pushup(); return true; } bool remove(node*& cur, const T& val) { if (!cur) return false; if (val == cur->val) return remove_node(cur); bool res; if (cmp(val, cur->val)) { res = remove(cur->left, val), cur->pushup(); if (get_high(cur->right) - get_high(cur->left) >= 2) { // 失衡,LL / LR 型 cur = get_high(cur->right->right) >= get_high(cur->right->left) ? right_rotate(cur) : right_left_rotate(cur); } } else { res = remove(cur->right, val), cur->pushup(); if (get_high(cur->left) - get_high(cur->right) >= 2) { // 失衡,RR / RL 型 cur = get_high(cur->left->left) >= get_high(cur->left->right) ? left_rotate(cur) : left_right_rotate(cur); } } if (cur) cur->pushup(); return res; } ``` ### 适用场景 AVL 比起 OI 平衡树(Splay 和 Treap),常数还是比较小的。 我们可以发现 AVL 对于查询不作旋转,因此 AVL 适合修改少查询多的场景,因为 AVL 的查询和 BST 的常数完全一样。 ## Treap Treap 是 BST 与堆的结合。Treap 的节点额外定义了 `prio` 域,初始化为随机值。Treap 的每个节点除了满足 BST 的定义外,还要保证父节点的 `prio` 小于孩子的 `prio`。即:`val` 上维护 BST 性质,`prio` 上维护小根堆性质。 可以证明,对于 `prio` 维护小根堆性质后,复杂度期望 $O(\log n)$。 一种方法是利用 AVL 的左右旋方法来维护小根堆性质。 ### 操作 插入操作改成: ```cpp void insert(node*& cur, const T& val) { ... if (cmp(val, cur->val)) { insert(cur->left, val), cur->pushup(); if (get_prio(cur->left) < get_prio(cur)) cur = right_rotate(cur); // ADD } else { insert(cur->right, val); if (get_prio(cur->right) < get_prio(cur)) cur = left_rotate(cur); } cur->pushup(); } ``` 我们来讲解一下带 `ADD` 注释的这一行。因为小根堆里上面节点的优先级必须得小,而新插入的左节点却比根节点小,那就进行右旋操作,使得左儿子上提至根,就能维护小根堆性质了。 删除操作仿照 BST,但找到节点后删除时我们要分类讨论一下。 ```cpp bool remove_node(node*& cur) { if (!cur) return false; if (cur->cnt > 1) { cur->cnt--, cur->pushup(); return true; } if (cur->left || cur->right) { T val = cur->val; if (!cur->right || get_prio(cur->left) > get_prio(cur->right)) { cur = right_rotate(cur); remove(cur->right, val); } else { cur = left_rotate(cur); remove(cur->left, val); } return cur->pushup(), true; } return cur = nullptr, true; } ``` 若 `cur` 为非叶子节点,必须考虑删除以后让谁来当,由于是小根堆就让 `prio` 小的当。若左儿子 `prio` 大于右儿子,就对 `cur` 右旋让右儿子当根,反之亦然。 ### 适用场景 旋转 Treap 的好处是常数比较小,实现相对简单。但是旋转的 Treap 不能可持久化,也不能序列操作,所以更适合用在排名查询的可重集中。 ## FHQ-Treap FHQ-Treap,即无旋 Treap,通过分裂与合并来维护 Treap 性质。 ### 性质维护 如它的名字,FHQ-Treap 满足 Treap 的性质。但是,FHQ-Treap 采用不同的性质维护方法——分裂和合并。这就是它为什么可以维护区间操作。 其实 BST 这种数据结构天然支持分裂。我们实现两个函数,`lower_split` 表示把小于查询值和大于等于查询值的树分裂,`upper_split` 表示把小于等于查询值和大于查询值的树分裂。 > 注:市面上常见的 FHQ-Treap 写法是用 `lower_split(x - 1)` 替代 `upper_split(x)`。这样可以减少码量,但我本人喜欢这么写。 考虑如何实现 `lower_split`,令 `lower_split` 返回分裂后的两棵树。根据查询值搜索: 1. 当前值大于等于查询值。此时,当前节点的右子树的全部值大于查询值,归入第二棵树,对左子树进行分裂即可。 2. 当前值小于查询值。此时,当前节点的左子树的全部值小于查询值,归入第一棵树,对右子树进行分裂即可。 `upper_split` 将分类讨论中的大于等于改为大于,小于改为小于等于即可。 在常用实现中,由于 C++14 不支持解包,用引用返回两棵树比较方便。 ```cpp void lower_split(node* cur, const T& val, node*& x, node*& y) { if (!cur) return (void) (x = nullptr, y = nullptr); if (!cmp(val, cur->val)) { // cur->val >= val x = cur, lower_split(x->right, val, x->right, y); x->pushup(); } else { y = cur, lower_split(y->left, val, x, y->left); y->pushup(); } } void upper_split(node* cur, const T& val, node*& x, node*& y) { if (!cur) return (void) (x = nullptr, y = nullptr); if (val != cur->val && !cmp(val, cur->val)) { // cur->val >= val x = cur, upper_split(x->right, val, x->right, y); x->pushup(); } else { y = cur, upper_split(y->left, val, x, y->left); y->pushup(); } } ``` 合并操作是 FHQ-Treap 的重点。合并有点类似线段树的合并,但要维护 Treap 的堆性质。 合并函数接收两棵树,其中第一棵树的所有值小于第二棵树的所有值。合并时,只需将 `prio` 小的上提,递归合并其子树即可。 ```cpp node* merge(node* x, node* y) { if (!x || !y) return x ? x : y; if (x->prio < y->prio) { x->right = merge(x->right, y); return x->pushup(); } else { y->left = merge(x, y->left); return y->pushup(); } } ``` ### 操作 插入操作可以简单的多。我们把整棵树按插入值 `lower_split` 成两部分,则第一棵树中所有值小于等于插入值,第二棵树中所有值大于插入值,在两棵树之间新建节点,合并即可。 ```cpp void insert(const T& val) { if (!root) { root = new node(val); return; } node *x, *y; lower_split(root, val, x, y); root = merge(merge(x, new node(val)), y); } ``` 删除时,按删除值 `split` 成三段:小于删除值的、等于删除值的、大于删除值的。删除等于删除值的节点即可。 ```cpp bool remove(const T& val) { node *x, *y, *z; lower_split(root, val, x, z); upper_split(x, val, x, y); if (!y) return false; y = merge(y->left, y->right); root = merge(merge(x, y), z); return true; } ``` 查排名也不用递归了,直接按查询值 `upper_split`。由于排名是比它小的数的数量 $+1$,查第一棵树的 `size` 即可。 ```cpp int rank(const T& val) { node *x, *y; upper_split(root, val, x, y); int rnk = x ? x->size : 0; root = merge(x, y); return rnk + 1; } ``` ### 适用场景 FHQ-Treap 好写且码量小,可以维护序列,支持可持久化。但是它的常数基本是所有平衡树里最大的,卡常题慎重使用。 ## pbds 最后说一个毁三观的东西,上述这些普通平衡树都不用学,因为 GNU 提供了 pbds 库,其中包含了带排名操作的平衡树。 ```cpp #include <ext/pb_ds/assoc_container.hpp> #include <ext/pb_ds/tree_policy.hpp> using namespace __gnu_pbds; tree<pair<T, int>, null_type, less<pair<T, int>>, rb_tree_tag, tree_order_statistics_node_update> tr; ``` `pair` 的第一个元素存储数据,第二个元素该元素的标号,以维护可重。 详情可见 [OI Wiki](https://oi-wiki.org/lang/pb-ds/tree/),这里就不展开了。 # 维护序列 平衡树真正的用途。之前我们维护的都是权值,假如将下标作为权值,那么就能把一个序列上树,且中序遍历是原序列。 ## 区间操作 用 FHQ-Treap 的分裂操作把树裂开成 $[1,l-1],[l,r][r+1,n]$ 三段,然后对 $[l,r]$ 作修改。
正在渲染内容...
点赞
0
收藏
0