主页
搜索
最近更新
数据统计
赞助我们
系统公告
1
/
1
请查看完所有公告
题解:P3366 【模板】最小生成树
最后更新于 2025-06-15 18:57:41
作者
sieve
分类
题解
题解
P3366
复制 Markdown
查看原文
更新内容
# 最小生成树 ## 概念 我们先画一张连通图: 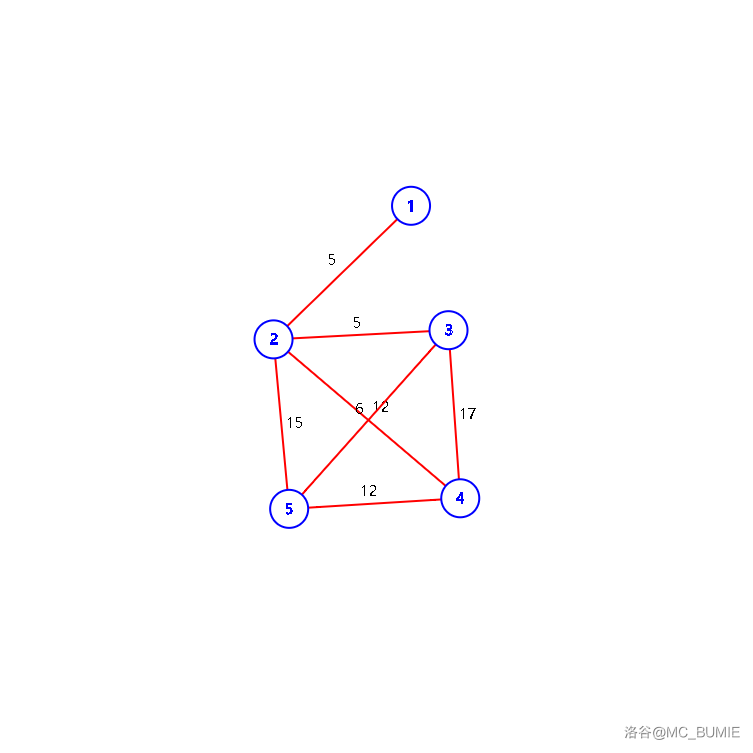 我们将图中的点标出来: 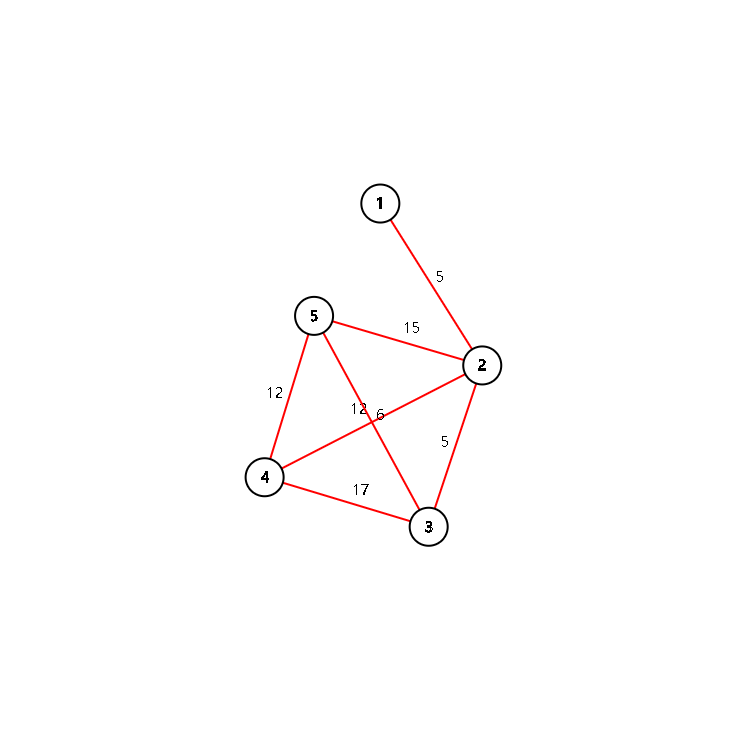 然后保证这些点能够两两之间互相连通的情况下,我们选择性的删去一些边,使得剩下的一棵树的所有边权之和最小。不过,既然是树,那么就不能有环。剩下的这棵树,我们就叫:最小生成树。注意:最小生成树的答案唯一,但是树并不唯一。 ## 最小生成树求法 ## Kruscal 这个算法就是用来求有 $n$ 个点,$m$ 条边的情况下的图的最小生成树,主要的涵盖算法有:贪心、并查集。 用到并查集的原因是需要判断是否成环。 ### Step 1: 我们先用两个变量 $sum$ 和 $cnt$ 来分别记录当前所选的边权之和、选了几条边。如果 $cnt = n - 1$ 也就是已经构成最小生成树了,就停止。 ### Step 2: 将建的边排序,按照边权从小到大排序。因为是要求最小生成树。 ### Step 3: 循环 $m$ 条边,每次取出两个端点,记作 $u$ 和 $v$ 。这时候,并查集就用上了,判断两个点的祖先是否相同,如果相同,则会构成环;否则将 $u$ 的祖先设为 $v$ ,然后 $sum$ 要加上这条边的权值,$cnt$ 加一。 ### Step 4: Kruscal 的时间复杂度:$O(m \log m)$。之所以有一个 $\log$ ,是因为你要排序。 ### Step 5: 实现: ```c++ void kruscal() { for(int i=1;i<=m;++i) { if(cnt==n-1) { break; } int u=find(a[i].x),v=find(a[i].y); if(u!=v) { sum+=a[i].z; cnt++; fa[u]=v; } } return; } ``` 仅为部分代码。
正在渲染内容...
点赞
0
收藏
0