浅谈 tarjan - 洛谷保存站

## 前言：
今天讲一下 tarjan，大家加油，一举攻破它。
## 何为 tarjan：
如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。\
~~言简意赅。~~
## 做法：
看了这言简意赅得介绍，其实就可以想到 DFS 了。不得不说，长得确实有几分相似。先给代码：
```cpp
void tarjan(int u){
	low[u]=dfn[u]=++ti;
	vis[u]=1;
	st.push(u);
	for(int i=0;i<g[u].size();i++){
		int v=g[u][i];
		if(!dfn[v]){
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]==1){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(low[u]==dfn[u]){
		++scc;
		while(!st.empty()){
			int t=st.top();
			op[scc].push_back(t);
			vis[t]=0;
			color[t]=scc;
			if(u==t){
				st.pop();
				break;
			}
			st.pop();
		}
	}
}
```
看上去确实有点像 DFS，有人就会问了：放一个 stack 干什么？$dfn,low,vis,color,scc$ 又是干什么的？我们慢慢讲。\
强连通的定义：在一个**有向**图中，每两个点都可以相互到达，如下图：\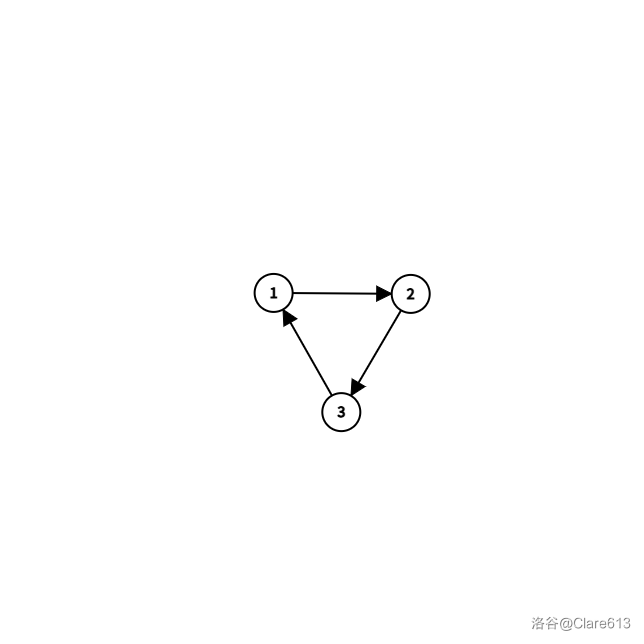
![](https://cdn.luogu.com.cn/upload/image_hosting/8c7ts9x3.png)\
弱连通的定义：在一个**有向**图中，每两个点不一定都可以相互到达，但转为无向图后两个点都可以相互到达，如下图：\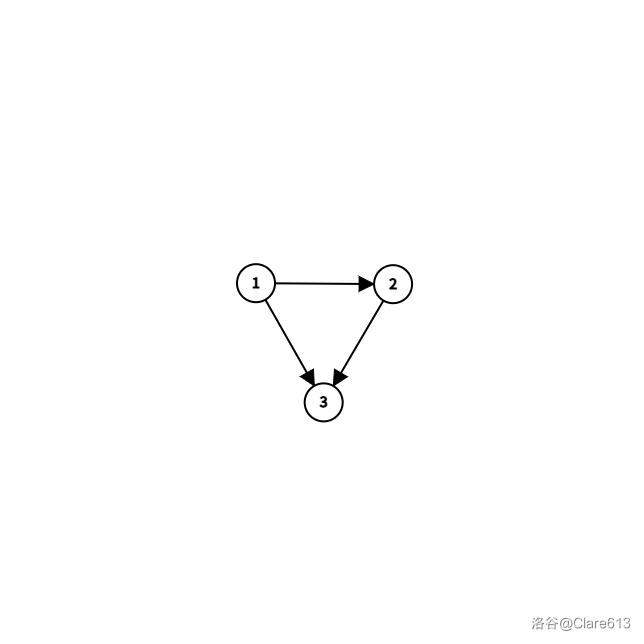
![](https://cdn.luogu.com.cn/upload/image_hosting/qhya82mx.png)\
前面的介绍讲了 tarjan 是用来求强连通分量的。我们可以发现，如果要求前连通分量，我们可以想象这张图像一条链一样，然后有个别几条边是往回跳的，那么就需要记录可以跳到的最远的点，编号（时间戳）即为 $dfn$，low 即为最远编号。如图：\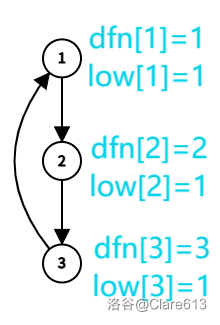
![](https://cdn.luogu.com.cn/upload/image_hosting/0yntcyu4.png)\
求出前连通分量后，我们可以记录下来，于是就有 $scc$（用于计数）、$color$（用于记录组别）、$st$（记录来的编号）、$vis$（记录是否在栈内）。
## 例题：

正在渲染内容...