树状数组

# [树状数组](https://oi-wiki.org/ds/fenwick/)
[题单](https://www.luogu.com.cn/training/756974#problems)
## 作用
快速**单点/区间修改**与**区间/单点查询**
## 原理
下图为树状数组工作原理

![原理](https://oi-wiki.org/ds/images/fenwick.svg)

最下面的 $8$ 个代表储存原始数据的 $a$ 数组,其他的表示用来存储前缀和的 $c$ 数组

> **为什么 $c$ 数组正好开 $n$ 个空间？**
> 
> 如下图所示，可以把 $c$ 数组连接成一个完全二叉树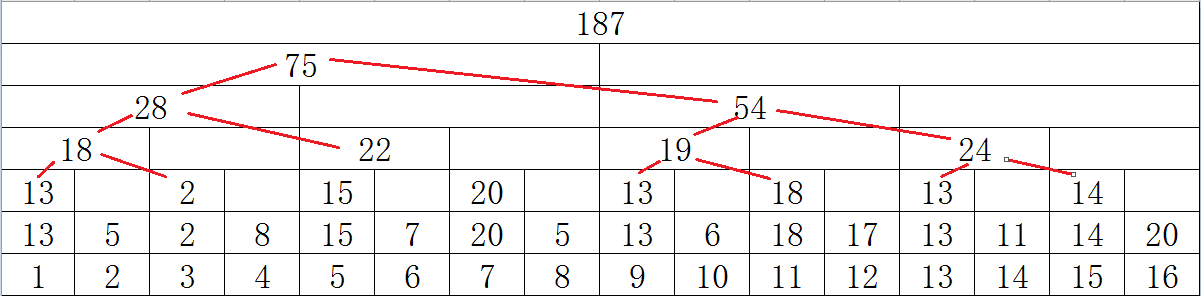
> 
> ![完全二叉树连接](https://cdn.luogu.com.cn/upload/image_hosting/7ipxu4dc.png)
> 
> 已知完全二叉树的节点个数为 $2^k-1$ ，加上最上边没有算上的 $187$ ，正好有 $2^k$ 个节点，且 $k=log_2(n)$
> 
> 将 $c$ 数组上面的数落下来，正好存 $n$ 个数

通过观察归纳可得， $c_i$ 的管辖区间长度恰好为 $i$ 二进制表示中，最低位的 $1$ 以及后面所有 $0$ 组成的数

也可以理解为将当前数二进制拆分，即可知道需要改变哪些数
## 代码
### 单点修改，区间查询
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,a[500001],c[500001];
int lowbit(int x){
	return x&(-x);
}//管辖区间长度
void upd(int x,int k){
	int i=x;
	while(x<=n){
		c[x]+=k;
		x+=lowb(x);
	}
	return;
}//更新数组
int getsum(int x){
	int sum=0;
	while(x>0){
		sum+=c[x];
		x-=lowbit(x);
	}
	return sum;
}//求结果
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[i]+=a[i-1];
		c[i]=a[i]-a[i-lowbit(i)];
	}
	for(int i=1;i<=m;i++){
		int b;
		cin>>b;
		if(b==1){
			int x,k;
			cin>>x>>k;
			upd(x,k);
		}else{
			int x,y;
			cin>>x>>y;
			cout<<getsum(y)-getsum(x-1)<<'\n';
		}
	}
	return 0;
}
```
### 区间修改，单点查询
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a[500001],d[500001];//求差分数组前缀和间接区间修改
int lowbit(int x){
	return x&(-x);
}
void upd(int x,int y){
	while(x<=n){
		d[x]+=y;
		x+=lowbit(x);
	}
	return;
}
long long getsum(int x){
	long long sum=0;
	while(x>0){
		sum+=d[x];
		x-=lowbit(x);
	}
	return sum;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=m;i++){
		int num;
		cin>>num;
		if(num==1){
			int x,y,k;
			cin>>x>>y>>k;
			upd(x,k);
			upd(y+1,-k);
		}else{
			int x;
			cin>>x;
			cout<<getsum(x)+a[x]<<'\n';//d数组只求了改变多少，结果需加上原数
		}
	}
	return 0;
}
```