题解：P11209 『STA - R8』小熊游景点 II

## 题意：
给定长度为 $n$ 的序列 $a,b$。

一共 $q$ 次询问，每次询问给定 $k$，你需要输出有多少 $i$ 满足 $a_i \oplus k\le b_i$。

## 题解：
对于异或问题，考虑字典树。

我们把关于 $a_i$ 和 $b_i$ 的 $k$ 放到字典树上，考虑 $k$ 在什么情况下会使得满足条件。

从高到低枚举位，

- 前 $j-1$ 位都一样，并且第 $j$ 位的 $b_i$ 是 $1$
  
我们发现只要 $k$ 与 $a_i$ 异或值为 $0$ 便一定满足条件，那么可以对这个节点打一个 $+1$ 的标记，只要询问的 $k$ 经过这里，那么就一定会产生这个贡献，并且已经不用再往下深入了，因为只要到了这个点就有贡献，与子树无关。

但是还要考虑如果这位的 $k$ 与 $a_i$ 异或也为 $1$ 的话那么就还需要继续考虑后面的位数，继续去看其他的节点是否可行。

-  前 $j-1$ 位都一样，并且第 $j$ 位的 $b_i$ 位是 $0$

那么此时只有当异或值位 $0$ 时才有可能能产生贡献，而异或值为 $1$ 时则一定不行，所以只需要考虑 $0$ 的情况即可。

并且我们需要对最后移位特判，因为等于这种情况也是可行的。

对于查询只需要按照 $k$ 的二进制从上往下走一遍将打的标记加起来就行了。

### 当 $a_i=0111$ 和 $b_i=0101$ 时举个例子。

- 对于最高位，只有 $k$ 这位等于 $0$ 才可能产生贡献，所以只建立一个 $0$ 的节点。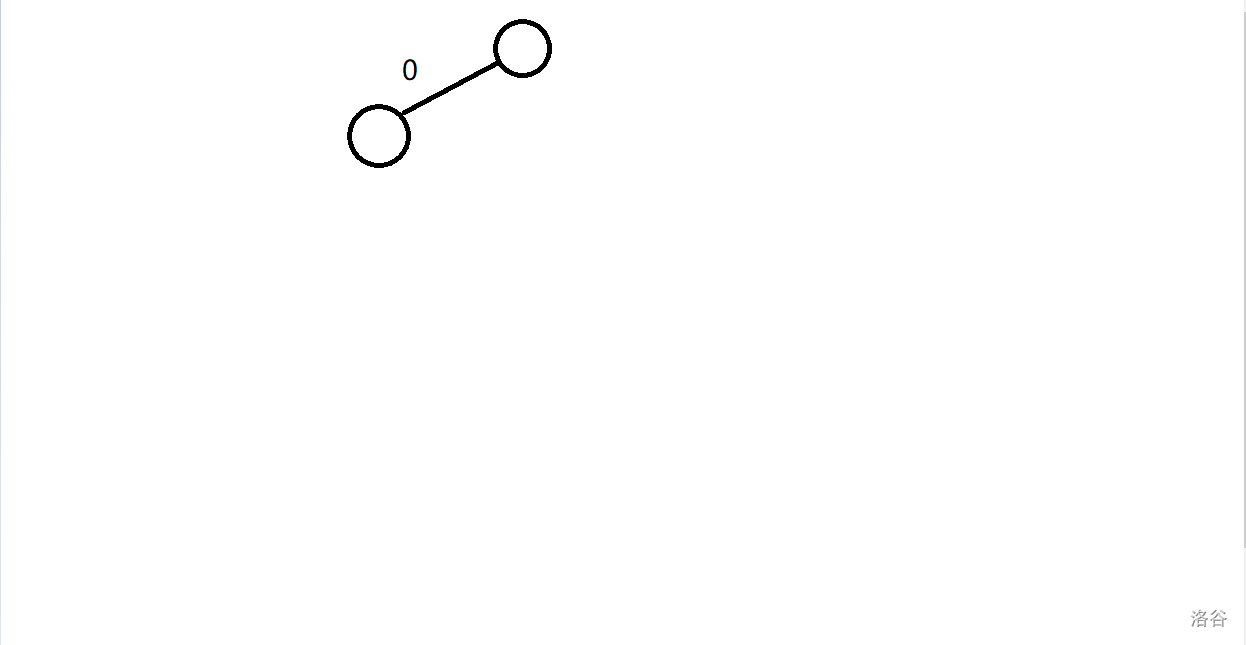
![](https://cdn.luogu.com.cn/upload/image_hosting/r1r9dlmz.png)

- 对于第二位，当 $k$ 这位等于 $1$ 时一定可行，所以在 $1$ 那里 $+1$。当 $k$ 这位等于 $0$ 时也可能可行，所以也要建立一个节点。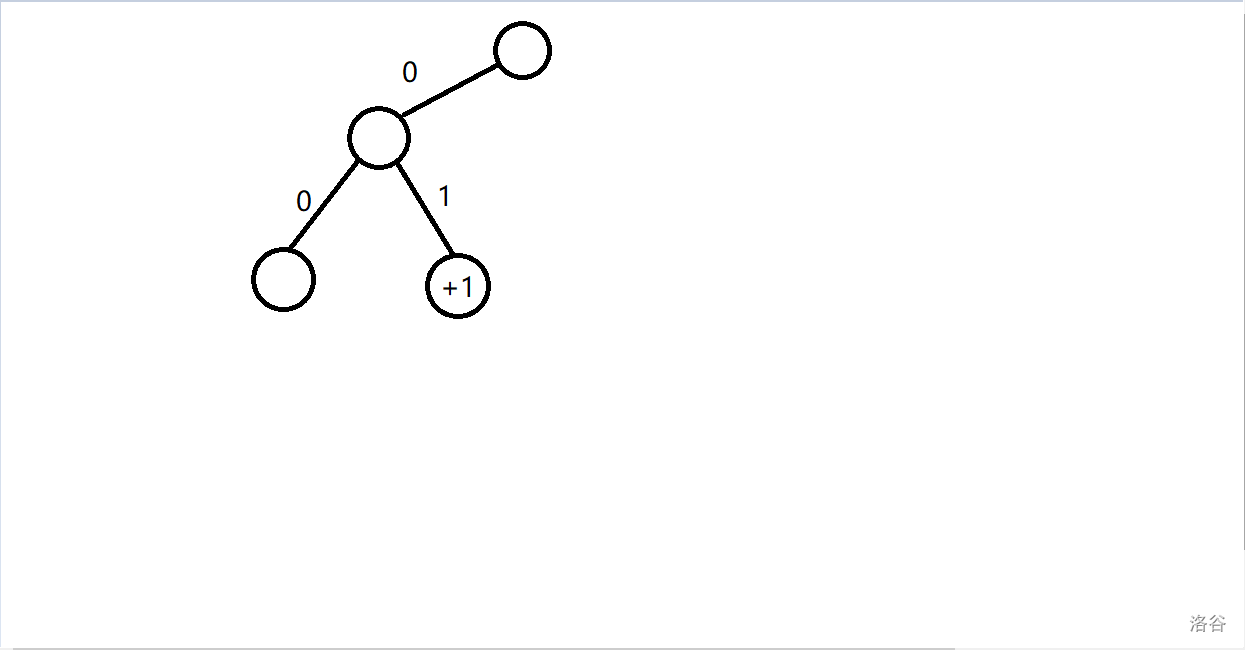
![](https://cdn.luogu.com.cn/upload/image_hosting/cevbr2w0.png)

- 对于第三位，只有 $k$ 这位等于 $1$ 时可能可行，所以往 $1$ 建立节点。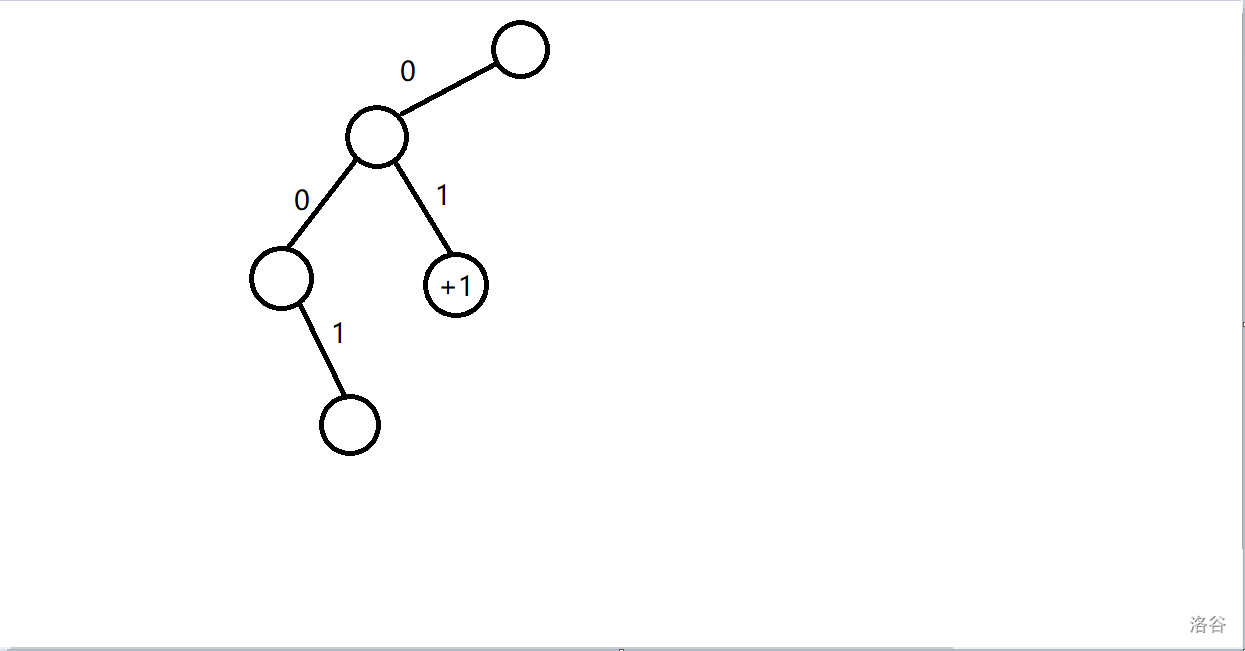
![](https://cdn.luogu.com.cn/upload/image_hosting/kw7hcy24.png)

- 对于最后一位，我们发现 $k$ 这位等于 $0$ 或 $1$ 都能产生贡献，所以都打一个 $+1$ 的标记。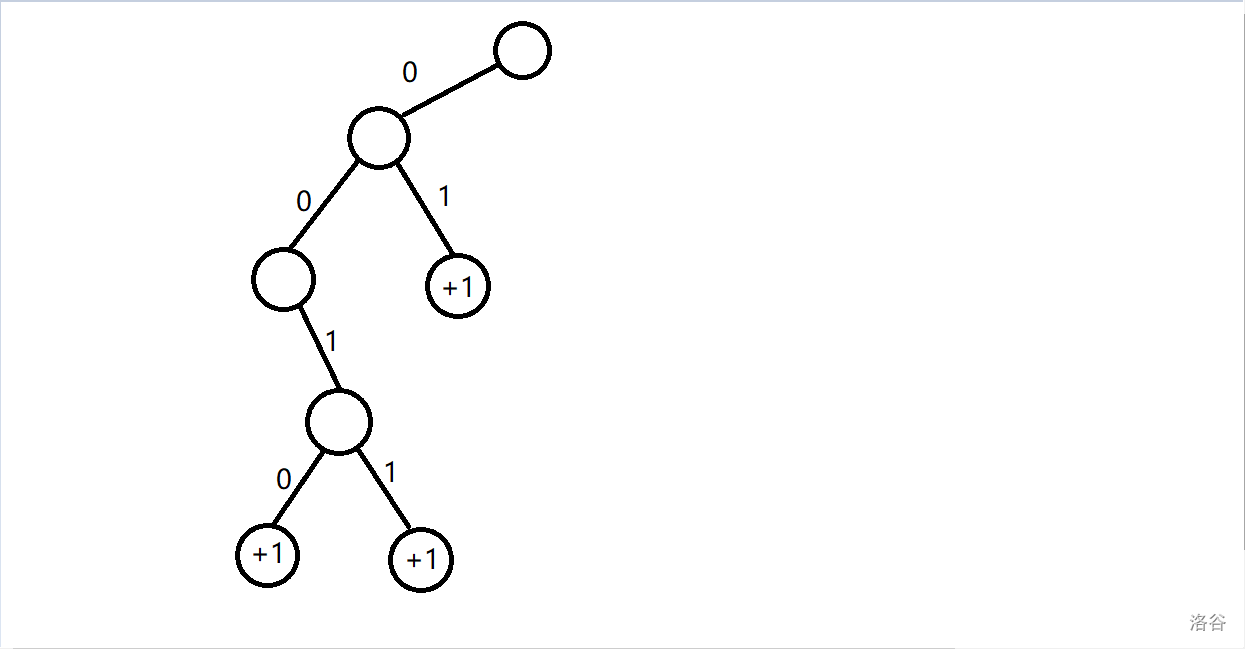
![](https://cdn.luogu.com.cn/upload/image_hosting/5k8l0sgp.png)

当 $k=15$ 时，$ans=0$。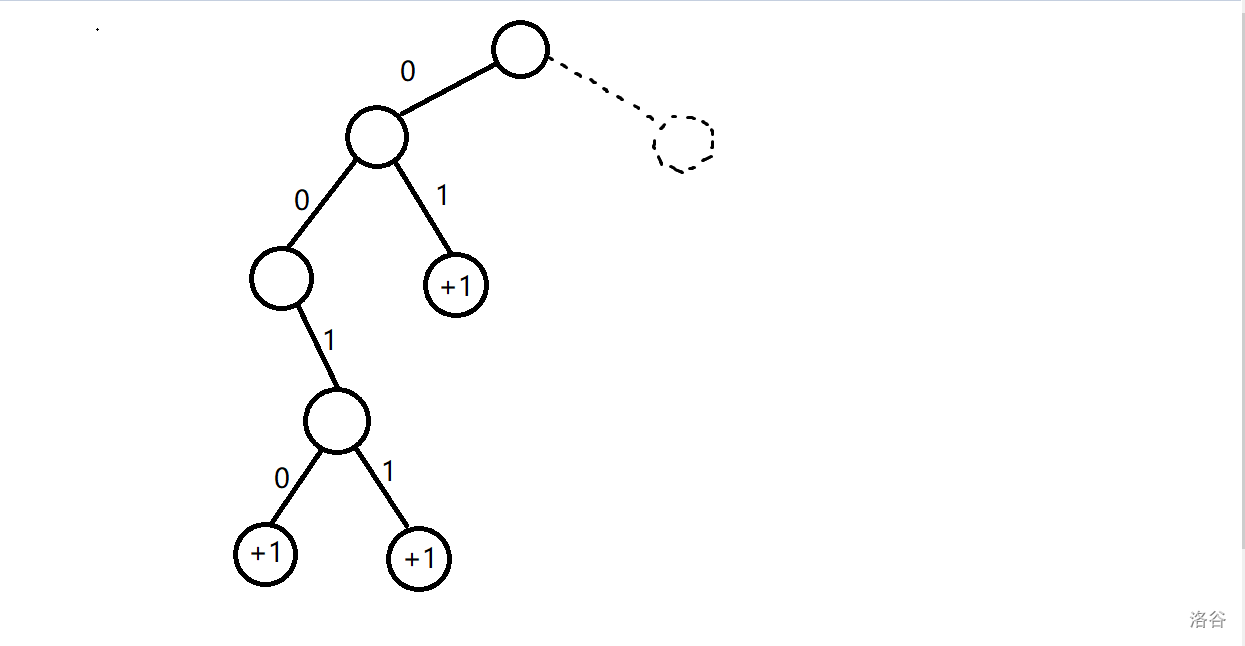
![](https://cdn.luogu.com.cn/upload/image_hosting/q0zyyevm.png)

当 $k=7$ 时，$ans=1$。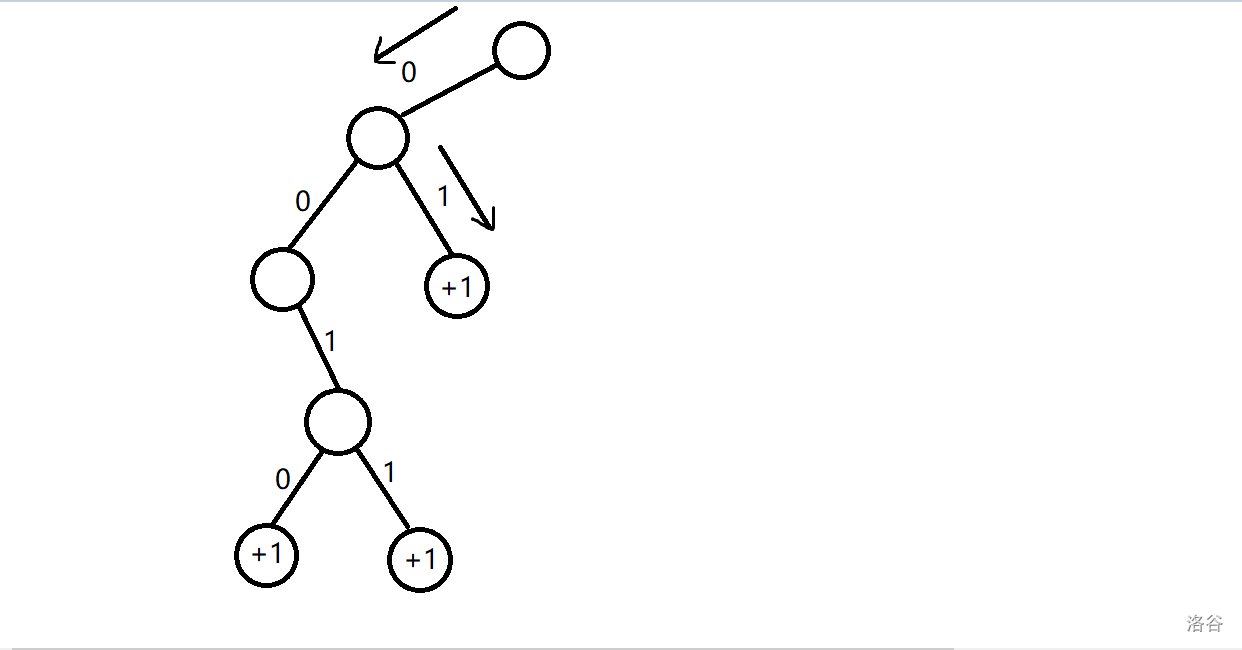
![](https://cdn.luogu.com.cn/upload/image_hosting/0dj3c9te.png)

当 $k=2$ 时，$ans=1$。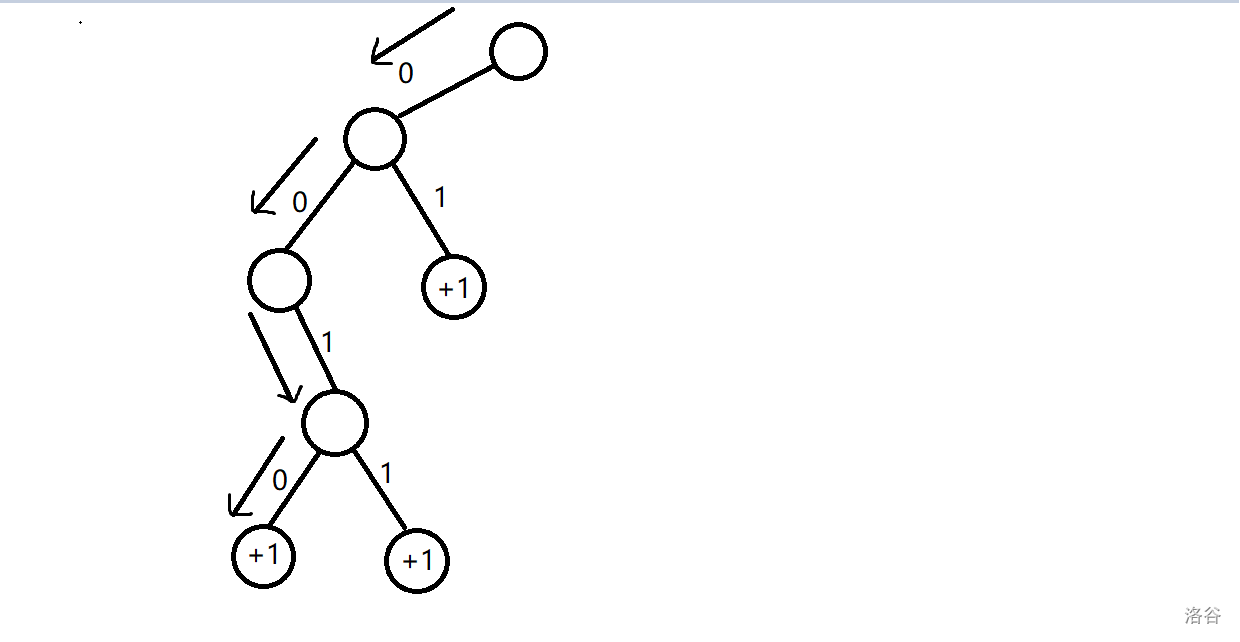
![](https://cdn.luogu.com.cn/upload/image_hosting/z87a6o3g.png)

## 复杂度：
建立节点时我们最多只会往一边去建立节点，所以是 $\log$ 的，而查询时也是只会走 $\log$ 层的，所以时间复杂度 $O(n\log v)$。

## code:
```cpp
#include<bits/stdc++.h>
using namespace std;

int tot;
int a[500010],b[500010];
struct Tree{
	int ch[2],val;
	Tree(){
		memset(ch,0,sizeof(ch));
	}
}tr[16000010];
int f=0;
void insert(int x,int y){
	int p=0;
	for(int i=31;i>=0;i--){
		int k1=(x>>i)&1,k2=(y>>i)&1,q;
		if(i==0){
			if(k2==0){
				q=k1;
				if(tr[p].ch[q]==0)
					tr[p].ch[q]=++tot;
				tr[tr[p].ch[q]].val++;	
			}else{
				q=k1;
				if(tr[p].ch[q]==0)
					tr[p].ch[q]=++tot;
				tr[tr[p].ch[q]].val++;	
				q=k1^1;
				if(tr[p].ch[q]==0)
					tr[p].ch[q]=++tot;
				tr[tr[p].ch[q]].val++;	
			}
			
			continue;
		}
		if(k2==1){
			q=k1;
			if(tr[p].ch[q]==0)
				tr[p].ch[q]=++tot;
			tr[tr[p].ch[q]].val++;
			q=k1^1;
			if(tr[p].ch[q]==0)
				tr[p].ch[q]=++tot;
			p=tr[p].ch[q];
		}else{
			q=k1;
			if(tr[p].ch[q]==0)
				tr[p].ch[q]=++tot;
			p=tr[p].ch[q];
		}
	}
}
int query(int x){
	int p=0,ans=0;
	for(int i=31;i>=0;i--){
		int q=(x>>i)&1;
		if(tr[p].ch[q])ans+=tr[tr[p].ch[q]].val,p=tr[p].ch[q];
		else break;
	}
	return ans;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	int T,n,q;
	cin>>T>>n>>q;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i],insert(a[i],b[i]);
	int lst=0;
	while(q--){
		int k;
		cin>>k;
		k=k^(lst*T);
		lst=query(k);
		cout<<lst<<'\n';
	}
	return 0;
} 
```

正在渲染内容...