2025.5.1 最后更新于 2025-05-01 20:32:27

# 数据结构 ## 上午 ### 队列 queue queue<int> q; queue<队列中存的类型>变量名 ``` q.push(233)//加入一个元素 q.pop()//删除第一个元素 int x=q.front()//查询第一个元素 q.size()//查询元素数量 ``` (bfs ### 双端队列 deque deque<int> q; deque<队列中存的类型>变量名 ```cpp q.push_front()//从前面加入 q.pop_front()//从前面删除 q.front()//询问前面第一个 q.push_back()//从后面加入 q.pop_back()//从后面删除 q.back()//询问后面第一个 ``` ### 单调队列 ```cpp void push(int i)//插入i { while（q.size()>0&&a[q.back()]>=a[i]) q.back_pop(); q.push_back(i); } ``` **典中典题**：$$给你一个序列，有n项，寻求一个区间使区间和小于等于 m，求区间范围最大的合法序列$$  ### 栈 stack stack<int> q; stack<栈中存的类型>变量名 ``` q.push(233)//加入一个元素 q.pop()//删除一个元素 233 int x=q.top()//获取栈顶元素 0 q.size()//查询元素数量 0 ``` (dfs ### 大根堆 priority_queue priorit_queue<int> q; 大根堆 ```cpp q.push(233)//加入一个元素 q.pop()//删除最大元素 233 int x=q.top()//获取最大元素 0 q.size()//查询元素数量 0 ``` ### 小根堆 priority_queue 全部取相反数即可 ### 并查集 本身是图论的内容，好像跟数据结构没设么关系 为了方便的查寻两个点是否在一个集合内  超绝$$O(n)$$并查集 ## 下午 ### Trie 字典树 存二进制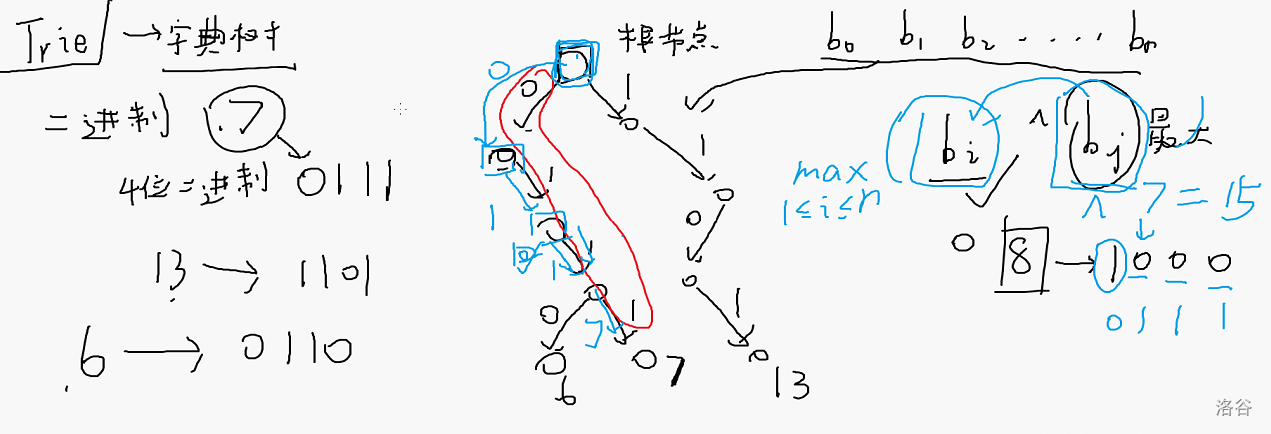：  准确来说这个叫$$01$$Trie #### 求$$a_1···a_n$$中两数异或后的最大值 代码： ```cpp struct node { int nxt[2];//nxt[0] nxt[1] 代表从当前点走0和1会走到哪里 走到0的话代表这个节点不存在 node() { nxt[0] = nxt[1] = 0; } }z[23333]; void insert(int x) { int p=root; for (int i=30;i>=0;i--) { int y=(x>>i)&1;//取出x二进制的第i位 if (z[p].nxt[y] == 0) {; cnt++; z[p].nxt[y] = cnt; } p = z[p].nxt[y]; } } int query(int x)//从trie中找一个数 使得他和x异或之后最大 { int p=root,ans=0; for (int i=30;i>=0;i--) { int y=(x>>i)&1; if (z[p].nxt[y^1] != 0) ans=ans|(1<<i),p=z[p].nxt[y^1]; else p=z[p].nxt[y]; } return ans; } int main() { root = 1; } ``` 核心思想：01Trie（能想到接下来就靠代码能力了 ### 分块 线段树平替，但慢 就是把一个段分成几个小块 #### 1.区间求和： 给定$$l,r$$,求$$a_l+···+a_r$$ 暴力：$$O（l-r）$$，太慢了 所以考虑分$$\sqrt n$$个块，每个里有$$\sqrt n$$个元素，这样最多走$$\sqrt n$$+几个点 #### 2.区间同加一个数 给定$$l,r,v$$，对$$a_l$$到$$a_r$$中的每个元素加$$v$$ 跟上边差不多，两边的散块暴力，中间的整块加坨大的然后均分给每个元素，打个懒标记的雏形 综合代码： ```cpp int belong[maxn];//belong[i] 代表第i个数属于第几块 int sum[maxn];//sum[i] 代表第i块的和是多少 int daxiao[maxn];//daxiao[i] 代表第i块的大小是多少 int col[maxn];//col[i] 代表第i块被整体加了col[i] int main() { cin >> n >> m; for (int i=1;i<=n;i++) cin >> a[i]; int s = sqrt(n);//每块的大小 for (int i=1;i<=n;i++) belong[i] = i/s+1; for (int i=1;i<=n;i++) { sum[belong[i]] += a[i]; daxiao[belong[i]] ++; } for (int x=1;x<=m;x++) { int opt; cin >> opt; if (opt == 1)//询问操作 { int l,r; cin >> l >> r; int ans=0; if (belong[l] == belong[r]) for (int i=l;i<=r;i++) ans += a[i] + col[belong[i]]; else { for (int i=l;belong[i] == belong[l]; i++) ans += a[i] + col[belong[i]]; for (int i=r;belong[i] == belong[r]; i--) ans += a[i] + col[belong[i]]; for (int i=belong[l] + 1; i < belong[r]; i++) ans += sum[i]; } cout << ans << "\n"; } else { int l,r,v; cin >> l >> r >> v; if (belong[l] == belong[r]) for (int i=l;i<=r;i++) a[i] += v; else { for (int i=l;belong[i] == belong[l]; i++) a[i] += v,sum[belong[i]] += v; for (int i=r;belong[i] == belong[r]; i--) a[i] += v,sum[belong[i]] += v; for (int i=belong[l] + 1; i < belong[r]; i++) { sum[i] += v * daxiao[i]; col[i] += v; } } } } return 0; } ``` #### 应用一下 $$a_l$$到$$a_r$$之间有多少个数出现了偶数次（不包括0） ~~**据说是有个冤种看错题了**~~ 利用分块思想： ### 莫队 离线排序，上代码： ```cpp struct query { int l,r,id,ans; }q[maxn]; bool cmp1(const query &q1, const query &q2) { if (belong[q1.l] != belong[q2.l]) return belong[q1.l] < belong[q2.l]; else return q1.r < q2.r; } bool cmp2(const query &q1, const query &q2) { return q1.id < q2.id; } void ins(int x) { cnt[x] ++; if (cnt[x] % 2 == 0) ans++; else if (cnt[x] != 1) ans--; } void del(int x) { cnt[x] --; if (cnt[x] != 0) { if (cnt[x] % 2 == 0) ans++; else ans--; } } int main() { cin >> n >> m; for (int i=1;i<=n;i++) cin >> a[i]; for (int i=1;i<=m;i++) { cin >> q[i].l >> q[i].r; q[i].id = i; } int s = sqrt(n); for (int i=1;i<=n;i++) belong[i] = i/s+1; sort(q+1,q+m+1,cmp1); for (int i=q[1].l;i<=q[1].r;i++) ins(a[i]); q[1].ans = ans; for (int i=2;i<=m;i++)//O(Nsqrt(N)) { int l1=q[i-1].l,r1=q[i-1].r; int l2=q[i].l,r2=q[i].r; if (l1 < l2) for (int i=l1;i<l2;i++) del(a[i]); else for (int i=l2;i<l1;i++) ins(a[i]); if (r1 < r2) for (int i=r1+1;i<=r2;i++) ins(a[i]); else for (int i=r2+1;i<=r1;i++) del(a[i]); q[i].ans = ans; } sort(q+1,q+m+1,cmp2); for (int i=1;i<=m;i++) cout << q[i].ans << "\n"; return 0; } ``` ## 作业(做ing) https://www.luogu.com.cn/problem/P3378 https://www.luogu.com.cn/problem/P1886 https://www.luogu.com.cn/problem/P3528 https://www.luogu.com.cn/problem/P3372 https://www.luogu.com.cn/problem/P3373 https://www.luogu.com.cn/problem/P4113 https://www.luogu.com.cn/problem/P9753 https://www.luogu.com.cn/problem/P8306 https://www.luogu.com.cn/problem/P10471