【五一集训】模拟赛第一场题解

## T1 古同学参加编程比赛

白送的题，按照题意的条件模拟即可

```cpp
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;
int n;
int main()
{
	cin>>n;
	if(n%2==0 && n>10)
	{
		cout<<n/2;
		return 0;
	}
	if(n%2==1 && n<20)
	{
		cout<<n*3+1;
		return 0;
	}
	cout<<n;
    return 0;
}
```

## T2 收集宝石

考察排序，sort的应用，可以直接使用sort过，或者手写一个桶排序也可以。不理解桶排序的出门[右转哔哩哔哩桶排序](https://www.bilibili.com/video/BV1zT4y1Y7Mj/?spm_id_from=333.337.search-card.all.click&vd_source=e101df49c542863125a7f434ab1e44fb)

sort用法：
sort(a+n,a+m,cmp);
n和m为数组下标，表示需要排序的数组位置。
cmp为多关键字排序时使用.
例如：
```cpp
sort(A, A + 100, greater<int>()); //降序排列
sort(A, A + 100, less<int>()); //升序排列

```

```cpp
#include <bits/stdc++.h>
using namespace std;
int main(){
    int n,p[15555];
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i];
	}
	for(int i=1;i<=n;i++){
		sort(p+1,p+n+1);
		cout<<p[i]<<" ";
	}
	return 0;
}
```
## T3 数据分析
题目中所求解的 $|a_i - a_j|^2 = (a_i - a_j)^2$，这样我们可以不考虑绝对值。

对于 $40\%$ 的数据，由于此时 $n$ 较小，我们可以根据题意使用循环进行模拟就可以了，枚举 $i,j$ 后直接求得答案，时间复杂度 $O(n^2)$。

```cpp
//40分做法
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,a[1005],ans=0;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			ans+=abs(a[i]-a[j])*abs(a[i]-a[j]);	
		}
	}
	cout<<ans;
	return 0;
}
```
对于 $100\%$ 的数据

$(a_i - a_j)^2 = a_i^2 + a_j^2 - 2 \times a_i \times a_j$。于是我们将所求的答案拆分为 $a_i^2 + a_j^2$ 与 $-2 \times a_i \times a_j$ 两部分。前一部分 $i$ 与 $j$ 独立，我们只需要对每一个 $i$ 求出它的贡献，即
$$
\sum_{i=1}^{n-1} \sum_{j=i+1}^n a_i^2 + a_j^2=\sum_{i=1}^n a_i^2 \times (n-1)
$$
对于后一部分
$$
\sum_{i=1}^{n-1} \sum_{j=i+1}^n -2 \times a_i \times a_j = \sum_{i=1}^{n-1} -2 \times a_i \times  \sum_{j=i+1}^n a_j
$$

总的来说

题目要求计算 $\sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} |a_i - a_j|^2$ 。

将 $|a_i - a_j|^2$ 展开得到 $(a_i - a_j)^2 = a_i^2 + a_j^2 - 2a_ia_j$ 。

我们可以想办法采用了一种巧妙的单重循环方式来避免双重循环的嵌套。在遍历数列元素的过程中：

对于每一个元素 $a_i$ ，先计算其自身平方项在整体结果中的贡献，即 $(n - 1) * a_i^2$ ，因为它要与除自身外的 $(n - 1)$ 个元素计算差值平方。

然后计算交叉项 $-2a_ia_j$ 的贡献，通过维护一个已读入元素的累加和 `sum` ，在每次读入新元素时，减去当前元素与已读入元素的交叉项贡献（这里乘以 2 是因为交叉项有 $a_ia_j$ 和 $a_ja_i$ 两种情况 ）。随着循环进行，依次处理每个元素，最终得到整个数列的差异程度值。

```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n, ans, sum; // 定义变量n表示数列长度，ans用于存储最终结果（差异程度），sum用于累加数列元素值

int main() {
    cin >> n; // 读取数列长度n
    for (ll i = 1; i <= n; i++) { // 遍历数列的每个元素
        ll x;
        cin >> x; // 读取当前元素值
        // 核心计算部分解释：
        // (n - 1) * x * x ：对于当前元素x，在计算差异程度的双重求和中，它与其他(n - 1)个元素都会产生差值的平方项。单独看x自身相关的贡献，它与其他元素差值平方展开后会有x * x这一项，且出现(n - 1)次，所以先加上(n - 1) * x * x
        // -x * sum * 2 ：在计算差值平方展开式中，会有 -2 * x * a_j （j ≠ i）这样的交叉项。而sum是之前所有元素的累加和，这里相当于减去当前元素x与之前所有元素交叉项的贡献，因为后面的元素还没读入，所以这里计算的是和前面已读入元素的交叉项情况
        ans += (n - 1) * x * x - x * sum * 2; 
        sum += x; // 将当前元素值累加到sum中，用于后续元素计算交叉项
    }
    cout << ans; // 输出最终计算得到的数列整体差异程度
    return 0;
}
```

换一种化简方法

题目要求计算$\sum_{i = 1}^{n - 1}\sum_{j = i + 1}^{n}|a_{i}-a_{j}|^{2}$ ，因为$|a_{i}-a_{j}|^{2}=(a_{i}-a_{j})^{2}=a_{i}^{2}-2a_{i}a_{j}+a_{j}^{2}$ 。

我们把这个双重求和展开来看：

先看$a_{i}^{2}$这一项的求和：

对于每一个$i$ ，从$i = 1$到$n - 1$ ，$j$从$i + 1$到$n$ 。当计算$a_{i}^{2}$的和时，对于固定的$i$ ，$j$有$n - i$种取值。那么$a_{i}^{2}$这一项的总和就是$\sum_{i = 1}^{n - 1}(n - i)a_{i}^{2}$ 。进一步可以发现，其实$a_{i}^{2}$总共会被加$n - 1$次（$i = 1$时，后面有$n - 1$个$j$ ；$i = 2$时，后面有$n - 2$个$j$ ，以此类推） ，同理$a_{n}^{2}$也会被加$n - 1$次，所以$a_{i}^{2}$这部分的总和其实就是$(n - 1)\sum_{i = 1}^{n}a_{i}^{2}$ 。

再看$a_{j}^{2}$这一项的求和：

和$a_{i}^{2}$类似，对于每一个$j$ ，$a_{j}^{2}$也会被加$n - 1$次，所以$a_{j}^{2}$这部分的总和也是$(n - 1)\sum_{j = 1}^{n}a_{j}^{2}$ ，因为$i$和$j$都是遍历整个数列，所以$(n - 1)\sum_{i = 1}^{n}a_{i}^{2}+(n - 1)\sum_{j = 1}^{n}a_{j}^{2}=n\sum_{i = 1}^{n}a_{i}^{2}$ （这里$n$个$a_{i}^{2}$相加）。

最后看$-2a_{i}a_{j}$这一项的求和：

我们把所有的$a_{i}a_{j}$（$i\neq j$ ）加起来。如果我们把$\sum_{i = 1}^{n}\sum_{j = 1}^{n}a_{i}a_{j}$展开，它等于$(\sum_{i = 1}^{n}a_{i})(\sum_{j = 1}^{n}a_{j})$ （这就像$(a_1 + a_2+\cdots+a_n)(a_1 + a_2+\cdots+a_n)$展开一样） ，而我们要求的$\sum_{i = 1}^{n - 1}\sum_{j = i + 1}^{n}a_{i}a_{j}$是$\sum_{i = 1}^{n}\sum_{j = 1}^{n}a_{i}a_{j}$去掉$i = j$时的$a_{i}^{2}$部分。$\sum_{i = 1}^{n}\sum_{j = 1}^{n}a_{i}a_{j}=(\sum_{i = 1}^{n}a_{i})^{2}$ ，$i = j$时的$a_{i}^{2}$部分就是$\sum_{i = 1}^{n}a_{i}^{2}$ 。所以$\sum_{i = 1}^{n - 1}\sum_{j = i + 1}^{n}(-2a_{i}a_{j})=- (\sum_{i = 1}^{n}a_{i})^{2}$ 。

综合起来，$\sum_{i = 1}^{n - 1}\sum_{j = i + 1}^{n}|a_{i}-a_{j}|^{2}=n\sum_{i = 1}^{n}a_{i}^{2}-(\sum_{i = 1}^{n}a_{i})^{2}$ 。

所以代码也可以写成这样

```cpp
#include<iostream>
using namespace std;
long long a[100001],s1,s2;
int n;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		s1+=a[i];
		s2+=a[i]*a[i];
	}
	cout<<n*s2-s1*s1;
}

//代码来自积分哥
```
## T4 获得合法摸鱼时长
找规律容易发现，对于所有 $n$ 都一定能表示（指用 $m_1,m_2,...$），不过不一定是 $k$ 个数。那我们可以求出最少和最多用多少个数表示，再看看能否累加或减少到 $k$ 个。

首先最多一定是 $n = 3^0 \times n$，最少则是 $n$ 在三进制下的非零数的个数，不妨设其为 $m$。如果 $m > k$，一定无解，$m = k$ 有解。$m < k$ 则需要尝试拆分调整。

观察到我们可以进行这样的拆分：$3^i = 3^{i-1} + 3^{i-1} + 3^{i-1}$，即进行这样的一次拆分可以使原本的 $m$ 增加 $2$。而 $n \ge k$，所有 $m$ 一直拆分下去，一定有一个时刻 $\ge k$。只需要判断 $m,k$ 的奇偶性是否相同即可。

```cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int T;
    cin >> T;
    while (T--) {
        long long n, k;
        cin >> n >> k;
        long long num = 0;
        while (n) {
            num += n % 3;
            n /= 3;
        }
        if (num > k)
            puts("No");
        else if ((k - num) % 2 == 0)
            puts("Yes");
        else
            puts("No");
    }
    return 0;
}

```

## T5 古同学要去露营
这是一道贪心题。假如这是一个数轴而非平面上的问题，最少的清除个数即为最远的两点中间的所有小方格。

但若在平面上，我们可以分为 $x,y$ 轴，合理猜想，答案为 $x$ 方向上的答案加上 $y$ 方向上的答案。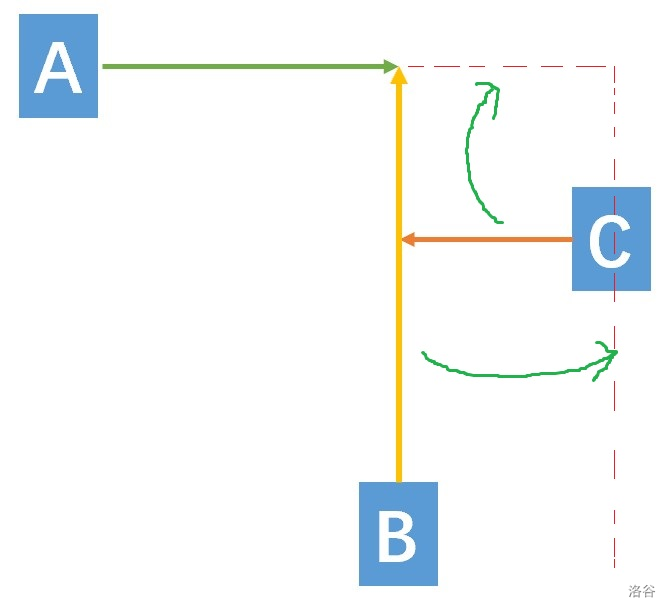

![无](https://cdn.luogu.com.cn/upload/image_hosting/a0gnlxjs.png)

即类似上图的关系，我们可以通过适当的平移，将红虚线部分移至橙线与黄线部分。

```cpp
#include <bits/stdc++.h>
using namespace std;
struct node {
    int x, y;
} a[5];
int Max(int a, int b, int c) { return max(max(a, b), c); }
int Min(int a, int b, int c) { return min(min(a, b), c); }
int main() {
	
    scanf("%d%d%d%d%d%d", &a[1].x, &a[1].y, &a[2].x, &a[2].y, &a[3].x, &a[3].y);
    printf("%d\n", Max(a[1].x, a[2].x, a[3].x) - Min(a[1].x, a[2].x, a[3].x) + Max(a[1].y, a[2].y, a[3].y) -
                       Min(a[1].y, a[2].y, a[3].y) + 1);
    return 0;
}

```

## T6 获取破解极域系统的秘密
首先考虑没有法术的情况，那么很显然，直接从左上角起点开始往右和下找，每次都取当前次字典序更小的那个字母，如果有多个相同的，就全部考虑进去，在下一步中将所有的这些点当作起点一起考虑。其实就是类似使用 `BFS` 处理的分层最短路。

当我们使用里法术之后呢？很显然，为了使最终的答案字典序最小，肯定将从起点开始，将经过的所有非字母 $a$ 的字母全部变为字母 $a$，这样得到的字典序最小。那么，我们将使用 $k$ 次法术最远能够到的地方全部计算出来，再用 `BFS` 的方法后半部分内容，也能找到对应的答案，具体如下。

如何统计使用 $k$ 次法术能到达的最远地方？我们可以使用 `dp`。定义 $f_{i,j}$ 表示从起点开始，到坐标 $(i,j)$ 的路径上，最少非 $a$ 字母数量。转移为 $f_{i,j} = \min(f_{i-1,j},f_{i,j-1}) + [(i,j) \not= 'a']$。

那么，只要 $f_{i,j} \le k$，我们就能使从起点开始到 $(i,j)$ 的路径上最后所有的小写字母均为 $a$。而我们要字典序最小，就需要找出符合要求的答案里边的值 $i+j$ 最大的那一些（即路径最长，前缀 $a$ 最多）。再从这些满足最大值的点开始进行 `BFS` 分层处理，就能找出最终字典序最小的序列。

```cpp
#include<bits/stdc++.h> 
using namespace std;
#define N 2050
// s[i][j]记录从起点(1,1)到位置(i,j)最少需要修改多少个字符
// f[i][j]记录是否存在一条路径经过位置(i,j)且路径上的字符修改次数不超过k
// n是表格的大小，即n行n列
int s[N][N],f[N][N],n; 
// a[i][j]存储表格中(i,j)位置的字符
// ans数组存储最终找到的字典序最小的路径字符串
char a[N][N],ans[N<<1];

// 初始化函数，处理输入、预处理字符修改，并通过动态规划找到最优路径
void init(){
    // 读取表格大小n和最多可修改的字符数k
    cin>>n;
    int k;
    cin>>k; 
    // 读取表格中每个位置的字符
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>a[i][j]; 
    
    // 第一阶段：预处理表格，尽可能将字符修改为'a'
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++){
            s[i][j]=0x3f3f3f3f; // 初始化为很大的值，表示不可达
            // 处理起点(1,1)
            if(i==1&&j==1){
                s[i][j]=(a[1][1]!='a'); // 如果起点不是'a'，则需要修改一次
                if(s[i][j]<=k) // 如果修改次数在允许范围内
                    a[i][j]='a'; // 就把起点字符改为'a'
                continue; 
            }
            // 从上方或左方转移过来，取修改次数较小的路径
            if(i>1) s[i][j]=min(s[i][j],s[i-1][j]); 
            if(j>1) s[i][j]=min(s[i][j],s[i][j-1]); 
            // 加上当前位置的修改次数
            s[i][j]+=(a[i][j]!='a'); 
            // 如果总修改次数不超过k，就把当前字符改为'a'
            if(s[i][j]<=k) a[i][j]='a'; 
        } 
    
    // 第二阶段：动态规划找出字典序最小的路径
    f[1][1]=1; // 起点可达
    ans[2]=a[1][1]; // 路径的第一个字符存入ans
    
    // 按路径长度从小到大处理每个可能的位置
    for(int k=3;k<=(n<<1);k++){
        char x='z'; // 初始化为最大字符，便于后续取最小值
        
        // 第一步：找出当前路径长度下所有可达位置中的最小字符
        for(int i=1;i<k;++i){
            int j=k-i; // 计算对应的列坐标
            if(j>n || i>n) continue; // 超出表格范围则跳过
            // 如果上方或左方位置可达，则更新最小字符
            if(f[i-1][j] || f[i][j-1]) 
                x=min(x,a[i][j]); 
        }
        
        // 第二步：标记所有可以使用最小字符的位置为可达
        for(int i=1;i<k;++i){
            int j=k-i;
            if(j>n || i>n) continue;
            // 如果当前位置的字符是最小字符，且上方或左方可达，则当前位置可达
            if(a[i][j]==x) 
                f[i][j]=(f[i-1][j] || f[i][j-1]); 
        }
        
        // 记录当前路径长度下的最小字符
        ans[k]=x; 
    }
    
    // 输出最终找到的字典序最小的路径
    for(int i=2;i<=(n<<1);i++)
        cout<<ans[i]; 
    cout<<"\n";
}

int main(){
    // 重定向输入输出文件
    freopen("treasure.in","r",stdin);
    freopen("treasure.out","w",stdout);
    init();
}
```

步骤：
1. **预处理阶段：尽可能多地将字符修改为'a'**
   - 遍历整个表格，计算从起点到每个位置的最小修改次数。如果某个位置可以通过不超过k次修改到达，就把该位置的字符改为'a'。
   - 这样做的目的是让路径上尽可能多的字符是'a'，因为'a'是字典序最小的字符。

2. **动态规划阶段：找出字典序最小的路径**
   - 按路径长度从小到大的顺序处理，每次处理时找出当前长度下所有可能位置中的最小字符。
   - 然后标记所有可以使用这个最小字符的位置为可达，并记录这个最小字符。
   - 这样逐步确定路径上的每个字符，保证整体路径的字典序最小。

3. **关键点解释**
   - **为什么要预处理字符修改？**：通过预处理，尽可能将路径上的字符变为'a'，从而在后续选择路径时能优先选择包含更多'a'的路径。
   - **如何保证字典序最小？**：在每个路径长度下，都选择当前能到达的位置中最小的字符，这样可以保证整体路径的字典序最小。
   - **为什么要分两步遍历？**：第一步找出最小字符，第二步标记可达位置，确保所有可能的路径都被考虑到。