2025 XYD Summer Camp 7.26 模考

时间线

• 8:30 开题先浏览了一遍题，坏了怎么有一百万道数学题，开始焦虑
• 决定按顺序写题，先做 T1，注意到横纵坐标可以分开处理，画了好久的图，最后发现线段树二分预处理就行了。
• 9:15 写完调完提交，开始看 T2，每走一条边相当于给某个二进制位加一，应该先把最高位对齐然后就可以直接一位位加了，写完发现过不了样例。感觉做不出来，跳 T3。
• 又推了很久式子，虽然觉得很可做但是有公式恐惧症，推到 10:00 红温了再跳题。
• 看 T4，一眼盯真，先这样在那样，随便杜教筛即可，非常开心，11:00 左右写完了。
• 最后一个小时狂砍 0pts，原因是在争 T2。

分数

题解

T1

给定一个以 $(0,0)$ 为左下角、$(n,m)$ 为右上角的平面和一个只包含 $\texttt{l,r,u,d}$ 四种字符的字符串 $S$。$Q$ 次询问，每次给定一个点 $(x,y)$，要求按顺序遍历 $S$ 中的每一个字符 $i$：

• 如果 $i=\texttt{u}$ 且 $y<m$，则 $y\gets y+1$；
• 如果 $i=\texttt{d}$ 且 $y>0$，则 $y\gets y-1$；
• 如果 $i=\texttt{l}$ 且 $x>0$，则 $x\gets x-1$；
• 如果 $i=\texttt{r}$ 且 $x<n$，则 $x\gets x+1$。

求最终得到的点 $(x’,y’)$。

$n,m,Q\le 2\times 10^5$。

考虑 $x$ 坐标与 $y$ 坐标的答案是独立的，所以可以分开计算。以计算 $x$ 为例，考虑预处理从每个 $x$ 开始的答案，对于 $\texttt{l}$ 操作，总是有一段前缀没有变化，剩下的整体减一；$\texttt{r}$ 则是对一段后缀无影响。直接线段树上二分得到每次操作的左右端点即可。时间复杂度 $O(n\log n)$。

int id, n, A, B, Q; string s;
const int maxn = 2e5 + 5;
vector<int> X, Y;
int mx[maxn << 2], mn[maxn << 2], col[maxn << 2];
void update(int rt) { mx[rt] = max(mx[rt << 1], mx[rt << 1 | 1]), mn[rt] = min(mn[rt << 1], mn[rt << 1 | 1]); }
void build(int l, int r, int rt) {
    col[rt] = 0;
    if (l == r) return mx[rt] = mn[rt] = l, void(0);
    int mid = (l + r) >> 1;
    build(lson), build(rson), update(rt);
} void color(int l, int r, int rt, int k) { mx[rt] += k, mn[rt] += k, col[rt] += k; }
void pushcol(int l, int r, int rt) {
    if (!col[rt]) return ;
    int mid = (l + r) >> 1;
    color(lson, col[rt]), color(rson, col[rt]), col[rt] = 0;
} int find_right(int l, int r, int rt) {
    if (l == r) return l;
    int mid = (l + r) >> 1; pushcol(l, r, rt);
    if (mn[rt << 1] > 0) return -1;
    if (mn[rt << 1 | 1] == 0)
        return find_right(rson);
    return find_right(lson);
} int find_left(int l, int r, int rt, int lim) {
    if (l == r) return l;
    int mid = (l + r) >> 1; pushcol(l, r, rt);
    if (mx[rt << 1 | 1] < lim) return lim + 1;
    if (mx[rt << 1] == lim) return find_left(lson, lim);
    return find_left(rson, lim);
} void modify(int l, int r, int rt, int nowl, int nowr, int k) {
    if (nowl > nowr) return ;
    if (nowl <= l && r <= nowr) return color(l, r, rt, k);
    int mid = (l + r) >> 1; pushcol(l, r, rt);
    if (nowl <= mid) modify(lson, nowl, nowr, k);
    if (mid < nowr) modify(rson, nowl, nowr, k);
    update(rt);
} int ans_x[maxn], ans_y[maxn];
int query(int l, int r, int rt, int now) {
    if (l == r) return mx[rt];
    int mid = (l + r) >> 1; pushcol(l, r, rt);
    if (now <= mid) return query(lson, now);
    return query(rson, now);
}
bool MemoryED; int main() { open(data);
    ios :: sync_with_stdio(0), cin.tie(0);
    cin >> id >> n >> A >> B >> Q >> s;
    for (int i = 0; i < n; i ++)
        if (s[i] == 'l') X.push_back(-1);
        else if (s[i] == 'r') X.push_back(1);
        else if (s[i] == 'u') Y.push_back(1);
        else if (s[i] == 'd') Y.push_back(-1);
    build(0, A, 1);
    for (int mov : X) 
        if (mov < 0) {
            int Right = find_right(0, A, 1);
            modify(0, A, 1, Right + 1, A, mov);
        } else {
            int Left = find_left(0, A, 1, A);
            modify(0, A, 1, 0, Left - 1, mov);
        }
    for (int i = 0; i <= A; i ++) ans_x[i] = query(0, A, 1, i);
    build(0, B, 1);
    for (int mov : Y) 
        if (mov < 0) {
            int Right = find_right(0, B, 1);
            modify(0, B, 1, Right + 1, B, mov);
        } else {
            int Left = find_left(0, B, 1, B);
            modify(0, B, 1, 0, Left - 1, mov);
        }
    for (int i = 0; i <= B; i ++) ans_y[i] = query(0, B, 1, i);
    for (int i = 1, x, y; i <= Q; i ++) 
        cin >> x >> y, cout << ans_x[x] << ' ' << ans_y[y] << '\n';
    return 0;
}

T2

对于数轴正方向（包括原点）的两个点 $x,y$，$x,y$ 之间有无向边当且仅当 $x,y$ 分别可以表示成 $a2^k,(a+1)2^k$ 的形式，其中 $a,k$ 均为非负整数。$T$ 次询问，每次给定 $x,y$，求 $x$ 到 $y$ 的最短路。

$T\le 5\times 10^5$，$x,y\le 10^{17}$。

考虑当 $x=0$ 时怎么做。此时如果 $y$ 是 $2$ 的幂次那么一步就可以到达，否则假设有 $2^k<y<2^{k+1}$，$y$ 可以选择走到这两个点之一，然后到达 $1$。从 $y$ 走到 $2^k$ 相当于从 $y-2^k$ 走到 $0$，同理从 $y$ 走到 $2^{k+1}$ 相当于从 $2^{k+1}-y$ 走到 $0$（因为这些点之间的连边情况都是一样的），于是可以进行递归，时间复杂度就是 $O(n)$ 的。

对于 $x<y$ 两个点，我们考虑从 $[0,2^{62}]$ 开始，每次取这个区间的中点分成左右两半，如果 $x,y$ 都在同一半则递归到这一半里，直到 $x,y$ 在两边。这样我们就会得到一个区间 $[L,R]$ 满足 $L\le x\le \frac{L+R}{2}\le y\le R$。注意到 $L,R$ 总是可以表示成 $2^ka$ 和 $2^k(a+2)$ 的形式（其中 $a$ 是偶数，证明考虑归纳），因此其中点就可以表示成 $M=2^k(a+1)$ 的形式；且 $L,M,R$ 都可以花 $1$ 的代价互相到达。

按照 $x=0$ 的结论，此时有两种路径：

• 从 $x$ 走到 $L$，再到 $R$，再从 $R$ 到 $y$。此时可以转化为：从 $0$ 走到 $x-L$、从 $0$ 走到 $R-y$。
• 从 $x$ 到 $M$ 再到 $y$，此时可以转化为：从 $0$ 走到 $M-x$、从 $0$ 走到 $y-M$。

两种方案中选一种小的即可。时间复杂度 $O(T\log n)$。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
unordered_map<ll, int> tab;
bool MemoryED; int main() {
    auto trans = [&](auto self, ll pos) -> int {
        if (pos == 0) return 0;
        ll high; for (high = 1ll << 62; high; high >>= 1ll)
            if (pos & high) break;
        if (pos == high) return 1;
        if (tab.find(pos) != tab.end()) return tab[pos];
        int &ans = tab[pos]; ans = inf;
        chkmin(ans, 1 + self(self, pos - high));
        chkmin(ans, 1 + self(self, (high << 1ll) - pos));
        return ans;
    }; 
    int T; for (cin >> T; T --; ) {
        ll x, y; cin >> x >> y;
        if (x == y) { puts("0"); continue; }
        if (x > y) swap(x, y);
        ll L = 0, R = 1ll << 62, M;
        for (; ; ) {
            M = (L + R) >> 1ll;
            if (L <= x && x <= M && L <= y && y <= M) R = M;
            else if (M <= x && x <= R && M <= y && y <= R) L = M;
            else break;
        } 
        // cout << L << ' ' << x << ' ' << M << ' ' << y << ' ' << R << '\n';
        cout << min(trans(trans, x - L) + 1 + trans(trans, R - y), trans(trans, M - x) + trans(trans, y - M)) << '\n';
    }
    return 0;
}

T3

$Q$ 次询问，每次给定正整数 $n$，求有多少种本质不同的周长为 $n$ 且边长是整数的三角形。

$Q\le 3\times 10^5$，$n\le 10^{10}$。

哎！这玩意是不是只和 $n$ 有关？打个暴力看看前几项然后拿到 OEIS 上跑一下，发现有公式： $$ \begin{cases}\left\lfloor\frac{(n+3)^2+24}{48}\right\rfloor&\text{ if }n\bmod 2=1\\left\lfloor\frac{n^2+24}{48}\right\rfloor&\text{ otherwise.}\end{cases} $$ 带入即可。时间复杂度 $O(Q)$。正经推导可以考虑分：等边、等腰、一般三角形分别进行计数，每次考虑枚举一个边，算出下一个边的范围，再展开得到 $O(1)$ 计算的表达式。

T4

基本题面是洛谷 P1014，但是跳过那些不是最简分数的分数进行标号，求一个分数 $x/y$ 的标号，若不是最简分数输出 $0$。

$x,y\le 10^9$。

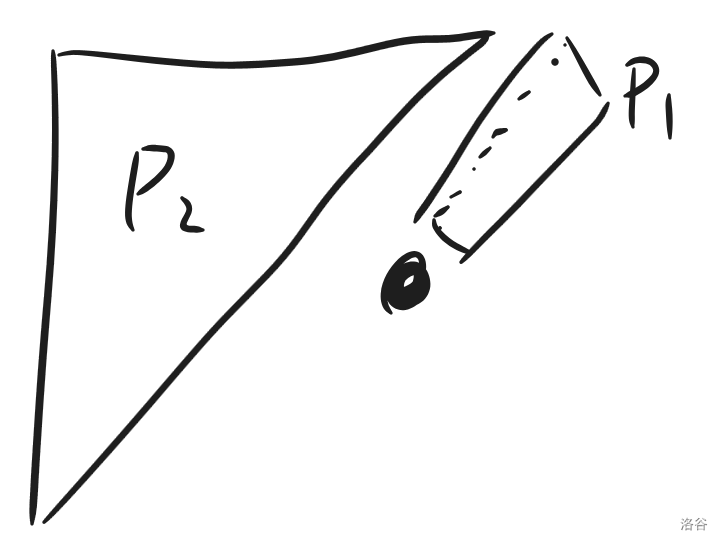
可以分成两部分计算：一个是图中 $P_1$ 的最简分数的数量，一个是 $P_2$ 的最简分数数量。加起来就是图中黑点的编号。

P1

记 $s=x+y$，也就是求 $$ \begin{aligned}\sum_{i+j=s,i\le x}[\gcd(i,j)=1]&=\sum_d\mu(d)[d\mid s]\left\lfloor \frac xd\right\rfloor\end{aligned} $$ 注意到这个式子只有在 $d$ 是 $s$ 的因子时有值，因此可以先把 $s$ 进行质因数分解，然后用枚举质因数的办法 $O(\sqrt n)$ 算这部分的答案。

P2

记 $s=x+y-1$，也就是求 $$ \begin{aligned}\sum_{i+j\le s}[\gcd(i,j)=1]&=\sum_{d}\mu(d)\sum_{i+j\le\lfloor s/d\rfloor}1\&=\sum_d\mu(d)\sum_{i=1}^{\lfloor s/d\rfloor}\left\lfloor\frac sd\right\rfloor-i\&=\sum_d\mu(d)\frac{\lfloor \frac sd \rfloor\left(\left\lfloor\frac sd\right\rfloor-1\right)}2\end{aligned} $$ 杜教筛即可。时间复杂度 $O(n^{2/3})$。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
int T; int gcd(int x, int y) { return y == 0 ? x : gcd(y, x % y); } 
const int N = 2e6, maxn = N + 5;
int mu[maxn], p[maxn >> 2], cnt; bool vis[maxn]; int sum[maxn];
void init() {
    mu[1] = 1;
    for (int i = 2; i <= N; i ++) {
        if (!vis[i]) mu[p[++ cnt] = i] = -1;
        for (int j = 1; 1ll * i * p[j] <= N && j <= cnt; j ++) {
            vis[i * p[j]] = 1, mu[i * p[j]] = -mu[i];
            if (i % p[j] == 0) { mu[i * p[j]] = 0; break; }
        }
    } for (int i = 1; i <= N; i ++) sum[i] = sum[i - 1] + mu[i];
} 
vector<pair<int, int> > res; int len; ll store;
void dfs(int now, int d, int mu_d, int x) {
    if (now >= len) return store += 1ll * mu_d * (x / d), void(0);
    dfs(now + 1, d, mu_d, x); 
    dfs(now + 1, d * res[now].first, -mu_d, x);
}
ll solve1(int x, int y) {
    int s = x + y - 1;
    if (s & 1) swap(x, y); res.clear(), len = 0; int tmp = s + 1;
    for (int i = 1; 1ll * p[i] * p[i] <= tmp; i ++) 
        if (tmp % p[i] == 0) {
            int c = 0;
            for (; tmp % p[i] == 0; c ++, tmp /= p[i]);
            res.emplace_back(p[i], c), len ++;
        }
    if (tmp > 1) res.emplace_back(tmp, 1), len ++;
    store = 0, dfs(0, 1, 1, x); return store;
} unordered_map<int, int> tab;
int solve(int n) {
    if (n <= N) return sum[n];
    if (tab.find(n) != tab.end()) return tab[n];
    ll ans = 1;
    for (int l = 2, r; l <= n; l = r + 1) {
        r = n / (n / l);
        ans -= 1ll * (r - l + 1) * solve(n / l);
    } return tab[n] = ans;
} ll f(int x) { return 1ll * x * (x - 1) >> 1; }
ll solve2(int x, int y) {
    int s = x + y - 1; ll ans = 0;
    for (int l = 1, r; l <= s; l = r + 1) {
        r = s / (s / l);
        ans += 1ll * (solve(r) - solve(l - 1)) * f(s / l);
    } return ans;
}
bool MemoryED; int main() { // open(data);
    for (init(), scanf("%d", &T); T --; ) {
        int x, y; scanf("%d %d", &x, &y);
        if (gcd(x, y) != 1) { puts("0"); continue; }
        printf("%lld\n", solve1(x, y) + solve2(x, y));
    }
    return 0;
}