浅谈数学——从矩形折叠板子看四种解法

# 前言

上次月考写了两篇博客，rp += inf 拿到年级 rk1。周二期末考，写一篇，加 rp。

# 问题
如图，在平面直角坐标系内，$A(4,0), B(0,3), C(4,3)$，将 $\triangle CAO$ 沿 $CO$ 翻折到 $\triangle CA'O$。求点 $A'$ 的坐标。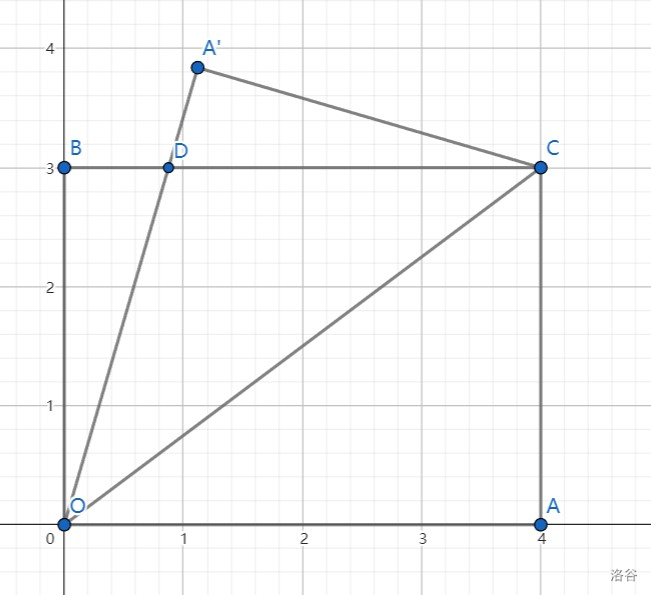

![](https://cdn.luogu.com.cn/upload/image_hosting/tpegjh0v.png)

# 解法一：对称点公式

这是一个秒杀的方法。需要知道对称点公式：

点 $(x,y)$ 关于 $y=kx+b$ 的对称点为 $(x-2k\dfrac{kx+b-y}{k^2+1},y+2\dfrac{kx+b-y}{k^2+1})$。

解：设 $OC:y=kx(k \ne 0)$，将 $C(4,3)$ 代入得 $4k=3$，解得 $k=\dfrac{3}{4}$，所以 $OC:y=\dfrac{3}{4}x$。

由对称点公式得 
$$
x_{A'}=x-2k\dfrac{kx+b-y}{k^2+1}=4-2\times\dfrac{3}{4}\times\dfrac{\dfrac{3}{4}\times4-0}{(\dfrac{3}{4})^2+1}=\dfrac{28}{25}
$$

$$
y_{A'}=y+2\dfrac{kx+b-y}{k^2+1}=0+2\times\dfrac{\dfrac{3}{4}\times4-0}{(\dfrac{3}{4})^2+1}=\dfrac{96}{25}
$$

所以 $A'(\dfrac{28}{25},\dfrac{96}{25})$。

# 解法二：建系

其实本题也可以暴力一点。我们连接 $AA'$，利用 $k_1k_2=-1$ 和中点坐标公式求解。

解：连接 $AA'$ 交 $CO$ 于点 $E$，由折叠知 $AE=A'E, AA' \bot CO$。

设 $OC:y=kx(k \ne 0)$，将 $C(4,3)$ 代入得 $4k=3$，解得 $k=\dfrac{3}{4}$，所以 $OC:y=\dfrac{3}{4}x$。

因为 $AA' \bot CO$，所以 $k_{AA'}=-\dfrac{1}{k_{CO}}=-\dfrac{4}{3}$。

设 $AA': y=-\dfrac{4}{3}x+m$，将 $A(4,0)$ 代入得 $=-\dfrac{4}{3}\times4+m=0$，解得 $m=\dfrac{16}{3}$，所以 $AA': y=-\dfrac{4}{3}x+\dfrac{16}{3}$。

联立 $y=\dfrac{3}{4}x$ 与 $y=-\dfrac{4}{3}x+\dfrac{16}{3}$ ，解得 $x=\dfrac{64}{25}, y=\dfrac{48}{25}$，所以 $E(\dfrac{64}{25},\dfrac{48}{25})$。

设 $A'(x, y)$，因为 $A'E=AE$，由中点坐标公式得 $\dfrac{x+4}{2}=\dfrac{64}{25}, \dfrac{y+0}{2}=\dfrac{48}{25}$，解得 $x=\dfrac{28}{25}, y=\dfrac{96}{25}$。

所以 $A'(\dfrac{28}{25},\dfrac{96}{25})$。

# 解法三：等腰 + 勾股

我的数学老师说过三句话：

> 平行 + 角分 = 等腰。

> 折叠的本质，就是找非重叠部分列勾股方程。

> 看到高，想到等面积和分类讨论。

解：由题 $BC \parallel AO$，则 $\angle COA = \angle DCO$。

由折叠知 $\angle DOC = \angle COA, A'C=AC=3, A'O=AO=4, \angle A'=\angle CAO = 90\degree$。

由 $\angle COA = \angle DCO, \angle DOC = \angle COA$ 得 $ \angle DCO=\angle DOC$，所以 $CD=DO$。

设 $A'D=x$，则 $CD=DO=A'O-A'D=4-x$。

在 $Rt \triangle A'DC$ 中，$\angle A' = 90 \degree$，   
由勾股定理得 $A'D^2+A'C^2=CD^2$，即 $x^2+3^2=(4-x)^2$，解得 $x=\dfrac{7}{8}$。

所以 $A'D=\dfrac{7}{8}, CD=4-x=4-\dfrac{7}{8}= \dfrac{25}{8}$。

所以 $S_{\triangle A'DE} = \dfrac{A'D \times A'C}{2} = \dfrac{\dfrac{7}{8} \times 3}{2} = \dfrac{21}{16}$。

过点 $A'$ 作 $A'E \bot DC$ 于点 $E$，如图：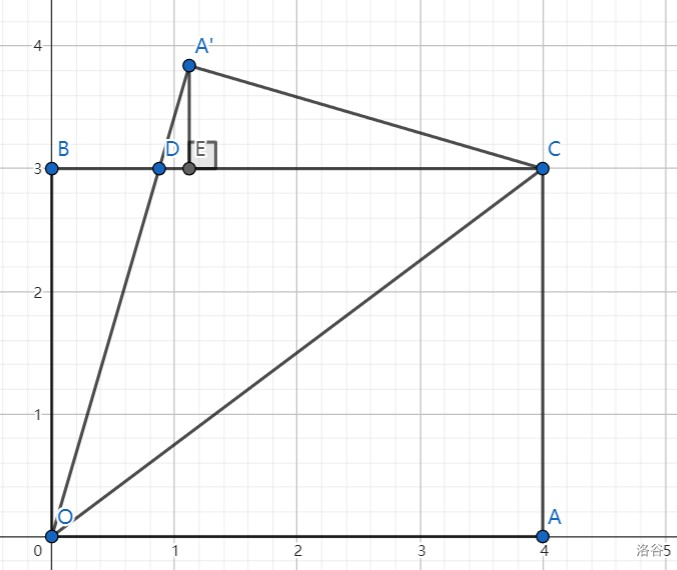

![](https://cdn.luogu.com.cn/upload/image_hosting/euq1guob.png)

又有 $S_{\triangle A'DE} = \dfrac{CD \times A'E}{2} = \dfrac{25}{16}A'E$，因为 $S_{\triangle A'DE}=\dfrac{21}{16}$，所以 $A'E=\dfrac{21}{25}$。

所以 $y_{A'} = y_C+A'E=3+\dfrac{21}{25}=\dfrac{96}{25}$。

在 $Rt \triangle A'EC$ 中，$\angle A'EC=90 \degree$，   
由勾股定理得 $CE=\sqrt{A'C^2-A'E^2}=\sqrt{3^2-(\dfrac{21}{25})^2}=\dfrac{72}{25}$。

所以 $x_{A'} = x_c-CE=4-\dfrac{72}{25}=\dfrac{28}{25}$。

所以 $A'(\dfrac{28}{25},\dfrac{96}{25})$。

# 解法四：特殊角科技

前置知识：[特殊角科技](https://www.luogu.com.cn/blog/stripe-python/the-magic-37-degree)。

解：在 $Rt \triangle CAO$ 中，$\angle CAO=90 \degree, AC=3, AO=4$，所以 $\angle COA = 37 \degree$。

由折叠知 $\angle DOC= \angle COA = 37 \degree, \angle A'=\angle CAO=90\degree$，则 $\angle BOD = 90 \degree - \angle COA - \angle DOC = 16 \degree$。

在 $Rt \triangle BOD$ 中，$\angle DBO = 90\degree$，所以 $\angle BOD+\angle BDO=90 \degree$。

在 $Rt \triangle DA'C$ 中，$\angle A' = 90\degree$，所以 $\angle A'CD+\angle A'DE=90 \degree$。

又因为 $\angle A'DE=\angle BDO$，所以 $\angle A'CD=\angle BOD= 16\degree$。

在 $Rt \triangle DA'C$ 中，$\angle A' = 90\degree, \angle A'CD=16\degree$，所以 $A'D:A'C:CD=7:24:25$。

由折叠知 $A'C=AC=3$，则 $A'D=\dfrac{7}{8}, CD=\dfrac{25}{8}$。

过点 $A'$ 作 $A'E \bot DC$ 于点 $E$，如图：

![](https://cdn.luogu.com.cn/upload/image_hosting/euq1guob.png)

易知 $\angle E'AD=16 \degree$，则 $A'E=24\dfrac{A'D}{25}=24\times \dfrac{\dfrac{7}{8}}{25}=\dfrac{21}{25}$。

所以 $y_{A'} = y_C+A'E=3+\dfrac{21}{25}=\dfrac{96}{25}$。

在 $Rt \triangle A'EC$ 中，$\angle A'EC=90 \degree, \angle A'CE=16\degree$，所以 $CE=24\dfrac{A'C}{25}=24\times \dfrac{3}{25}=\dfrac{72}{25}$。

所以 $x_{A'} = x_c-CE=4-\dfrac{72}{25}=\dfrac{28}{25}$。

所以 $A'(\dfrac{28}{25},\dfrac{96}{25})$。

# 方法对比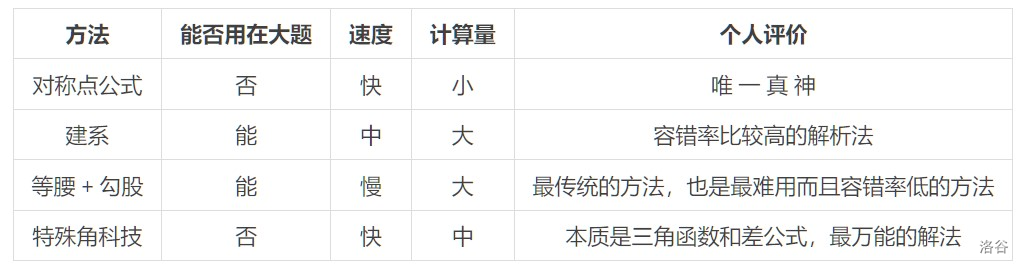

![](https://cdn.luogu.com.cn/upload/image_hosting/l81yjada.png)

正在渲染内容...