支配树及其应用学习笔记

# 支配树及其应用学习笔记

## 1.定义

**在本文中，如果 $dfn_x<dfn_y$ ，则称 $x<y$，其中 $dfn_x$ 为一颗深度优先搜索树中节点 $x$ 的遍历时间。**

$G(V,E)$ 为一个 $n$ 个点，$m$ 条边的有向图，其中 $V$ 为点集，$E$  为边集，且 $|V|=n,|E|=m$

在给定起点 $s$ 的情况下，如果任何从 $s$ 走到 $y$ 的路径上都要经过 $x$ ,那么称 $x$ 支配 $y$ 。

**性质1**：如果 $x$ 支配 $y$ 且 $y$ 支配 $z$ ,则 $x$ 支配 $z$ ，也即支配关系满足传递性。

证明显然

**性质 2**：如果 $x$ 支配 $y$ 且 $y$ 支配 $x$ ，则 $x$ = $y$ 。

显然

**性质 3**：如果 $x$, $y$,$z$ 互不相等，且 $x$ 和 $y$ 均支配 $z$ ，则必有 $x$ 支配 $y$ 或 $y$ 支配 $x$ 。

证明：

考察任意一条从 $s$ 到 $z$ 的简单路径，这条路径上必有 $x$ 和 $y$ ，不失一般性可以假设路径形如 $s, . . . , x, . . . , y, . . . ,z $。如果 $x$ 不支配 $y$ ，则存在一条不经过 $x$ 的 $s$ 到 $y$ 的路径， 此时若把前述路径从 $s$ 到 $y$ 的部分替换成这条不经过 $x$ 的路径，就得到了一条从 $s$ 到 $z$ 且不经过 $x$ 的路径了，而这和 $x$ 支配 $z$ 矛盾。

**直接支配点**：存在一个点 $z$ 满足：如果 $y \not = x$  支配 $x$ ， 则 $y$ 也支配 $z$ 。我们称 $z$ 是 $x$ 的直接支配点 (immediate dominator)，记为 $z = idom(x)$ 。

对于除 $s$ 外的所有点，连一条 $idom(x) → x$ 的边，建出来的就是支配树。

支配树满足若 $x$ 是 $y$ 的祖先，则 $x$ 支配 $y$ ，若 $x$ 不是 $y$ 的祖先，则 $x$ 不支配 $y$

由支配的传递性易证

## 2.求解支配树

### 2.1 半支配点

**定义**：点 x 的半支配点 $sdom(x) = min,y | 存在一条路径 y = v0, v1, . . . , vk = x 满足对于 任意 1 ≤ i ≤ k − 1 都有 vi > x$ 。

通俗来讲就是图上最小的点$y$ ,使得存在一条路径从 $y$ 到 $x$，路径中除了 $y$ 以外的节点都大于等于 $x$ 。

记为 $sdom(x)$

**定理1**：如果 $x ≤ y$ 则任意 $x$ 到 $y$ 的路径必须经过 $x$ 和 $y$ 在 DFS 树上的某个公共祖先。

**证明**：$x$ 是 $y$ 的祖先时结论显然，因此可认为 $x$ 不是 $y$ 的祖先。

如果 $x$ 到 $y$ 不经过 $x$ 和 $y$ 在 DFS 树上的某个公共祖先，那么在深搜时 $y$ 一定会在 $x$ 或 $x$ 的祖先且不是 $y$ 的祖先的子树内，此时 $x$ 到 $y$ 的路径必须经过  $x$ 和 $y$ 在 DFS 树上的某个公共祖先，矛盾。

**引理 2**：$idom(x)$ 和 $sdom(x)$ 都是 DFS 树上 $x$ 的祖先且不等于 $x$。更进一步地，在 DFS 树上 $idom(x)$ 是 $sdom(x)$ 的祖先。

**证明**：$idom(x)$ 在 DFS 树上是 $x$ 的祖先是显然的。

由于 $x$ 在 DFS 树上的父亲已经满足了半支配点的要求，所以有 $sdom(x) < x$ 。另一方 面，如果 $sdom(x)$ 不是 x 的祖先，则不难发现 $sdom(x)$ 在 DFS 树上的父亲也满足半支配点 的要求，且比 $sdom(x)$ 更小，这和半支配点的定义矛盾。

根据半支配点的定义，可以沿 DFS 树从 $s$ 走到 $sdom(x)$ 再沿定义所述的路径走到 $x$ 。 因此 DFS 树中，$sdom(x)$ 到 $x$ 的路径上（这里不包括 $sdom(x)$）的点均不支配 $x$ ，故 $idom(x)$ 一定是 $sdom(x)$ 的祖先。

**引理 3**：令 $v,w$ 满足 DFS 树上 $v$ 是 $w$ 的祖先，则 $v$ 是 $idom(w)$ 的祖先或 $idom(w)$ 是 $idom(v)$ 的祖先。

画图理解一下。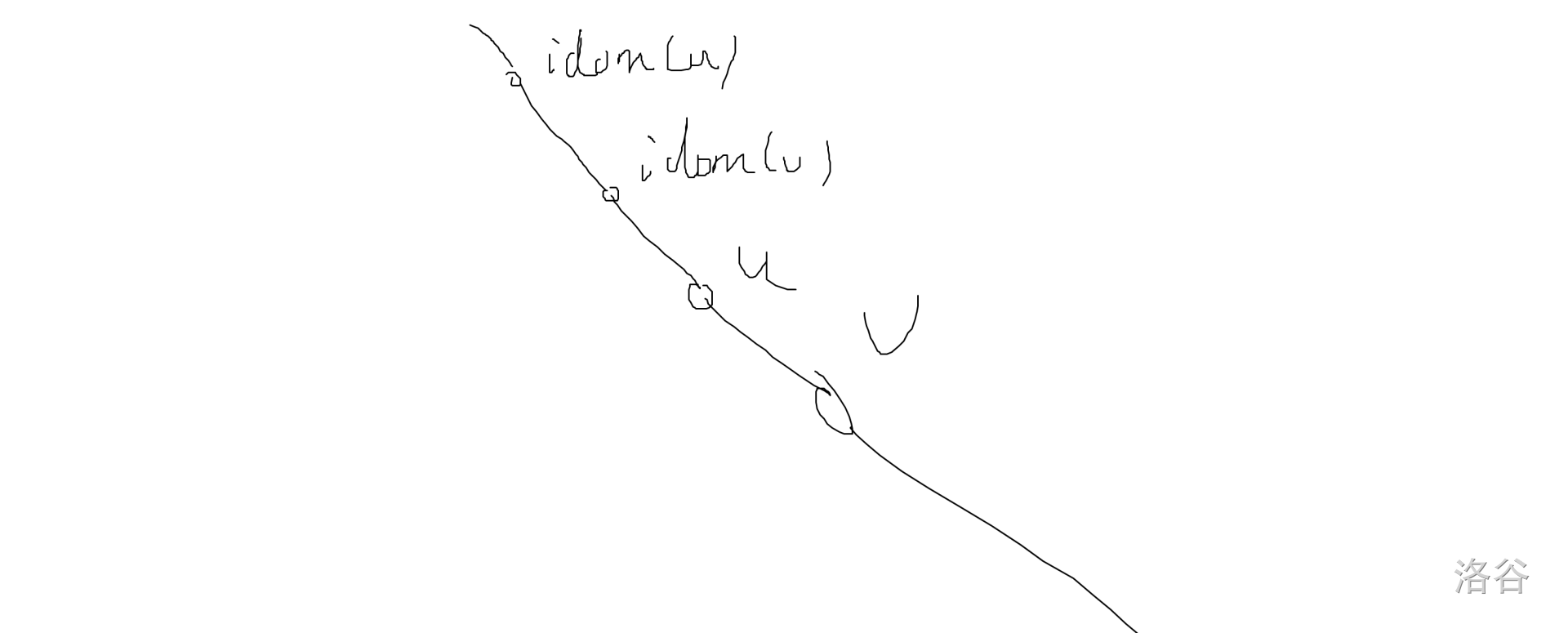

![](https://cdn.luogu.com.cn/upload/image_hosting/zu01pjct.png?x-oss-process=image)

意思就是不存在这种情况。

如果存在，就说明从 $s$ 到 $idom(v)$ 的路径中存在一条不经过 $idom(u)$ 的，不然 $idom(v)=idom(u)$ 。那么就可以找到这么一条路线 $s -> idom(v) - > u$ 且不经过 $idom(u)$ 。矛盾。

所以不存在这种情况。

**定理 2**：任取点 $w\not =s$ 。考虑 **DFS 树**上从 $sdom(w)$ 到 $w$ 的路径上（不包括 $sdom(w)$）的任意点 $y$，如果均满足 $sdom(y) ≥ sdom(w)$ ，则 $idom(w) = sdom(w)$ 。

继续画图。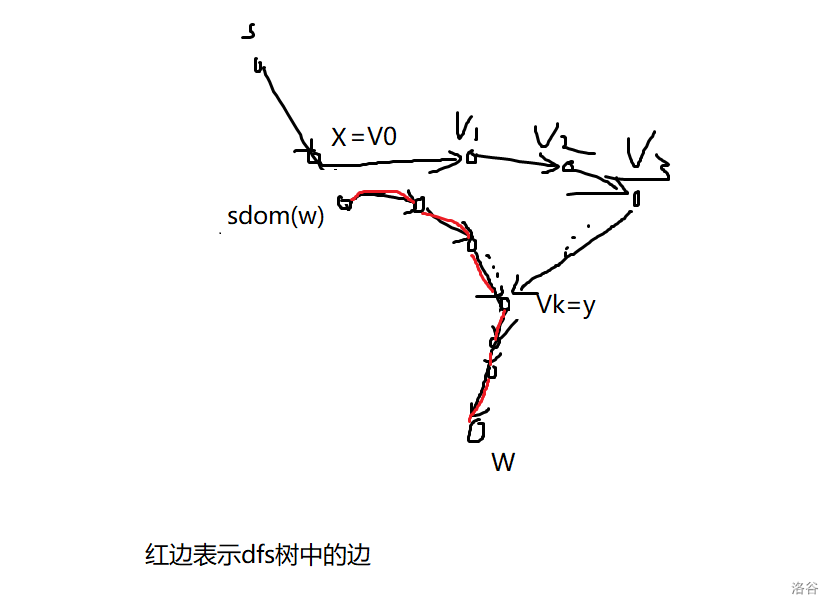

![](https://cdn.luogu.com.cn/upload/image_hosting/3z7kdy05.png?x-oss-process=image)

**证明**：根据引理 2，有 $idom(w)$ 是 $sdom(w)$ 的祖先，因此只需证 $sdom(w)$ 支配 $w$ 。考虑 任意一条 $s$ 到 $w$ 的路径 $P$ ，我们将要证明 $sdom(w)$ 一定在 $P$ 中。令 $x$ 是 $P$ 中最后一个满足 $x < sdom(w)$ 的点，如果不存在则必有 $sdom(w) = idom(w) = s$ ，结论仍然成立。同时，令 $y$ 是 P 中 $x$ 之后的第一个在 DFS 树中从 $sdom(w)$ 到 $w$ 的路径上的点。在 $P$ 中截取 $x$ 到 $y$ 之 间的部分得 $v0 = x, v1, . . . , vk = y$。

现在考虑路径 $v0, . . . , vk$ ，我们声称对于 $1 ≤ i < k$ 都有 $v_i > y$ ，也即 $sdom(y) ≤ x < sdom(x)$ 。若不满足这一点，则有某个 $vi < y$ ，此时根据**定理 1**可得存在某个 $i ≤ j ≤ k − 1$ 满足 $vj$ 是 $y$ 的祖先。由 $x$ 的取值可知 $sdom(w) ≤ vj$ ，于是 $v_j$ 也在 DFS 树中从 $sdom(w)$ 到 $w$ 的路 径上，这和 $y$ 的取值矛盾。上述矛盾可推得 $sdom(y) ≤ x < sdom(x)$ 。

结合定理的条件：从 $sdom(w)$ 到 $w$ 的路径上（不包括 $sdom(w)$）的任意点 $y$，均满足 $sdom(y) ≥ sdom(w)$ 。

必有 $y = sdom(w)$ ，即路径 P 包含 $sdom(w)$。

**定理 3**：任取点 $w \not=s$ 。考虑 DFS 树上从 $sdom(w)$ 到 $w$ 的路径上（不包括 $sdom(w)$）的 所有点，令 $u$ 是其中 $sdom$ 最小的点，则 $sdom(u) ≤ sdom(w)$ 且 $idom(u) = idom(w)$ 。

还是画图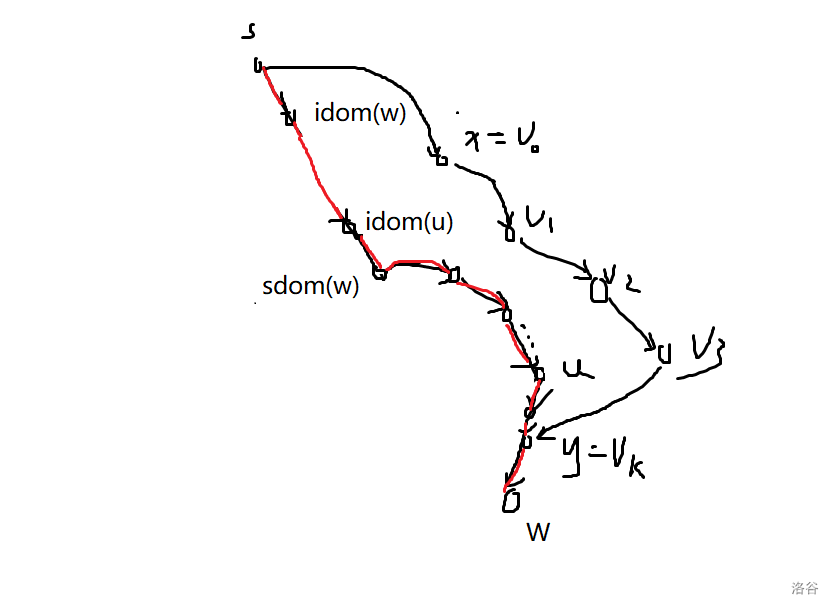

![](https://cdn.luogu.com.cn/upload/image_hosting/6m55sl4h.png?x-oss-process=image)

**证明**：由于 $w$ 也是 $u$ 的一个候选，$sdom(u) ≤ sdom(w)$ 是显然的。注意到在 DFS 树 上 $idom(w)$ 是 $u$ 的祖先，于是根据**引理 3 **可知 $idom(w)$ 也是 $idom(u)$ 的祖先，因此只需证 $idom(u)$ 支配 $w$ 。考虑任意一条 $s$ 到 $w$ 的路径 $P$ ，我们将要证明 $idom(u)$ 一定在 $P$ 中。令 $x$ 是 $P$ 中最后一个满足 $x < idom(u)$ 的点，如果不存在则必有 $idom(u) = idom(w) = s$ ，结论仍然成立。同时，令 $y$ 是 $P$ 中 $x$ 之后的第一个在 DFS 树中从 $idom(u)$ 到 $w$ 的路径上的点。 在 $P$ 中截取 $x$ 到 $y$ 之间的部分得 $v0 = x, v1, . . . , vk = y$。

和**定理 2** 的证明类似，我们可以得到 $sdom(y) ≤ x$ 。根据引理 2 有 $idom(u) ≤ sdom(u)$ ， 综合起来可得 $sdom(y) ≤ x < idom(u) ≤ sdom(u)$ 。至此，由 $u$ 的选择可知 $y$ 不能是 $sdom(w)$ 的除自身外的后代；另一方面，$y$ 不能既是 $idom(u)$ 的除自身外后代也是 $u$ 的祖先，否则沿 DFS 树从 $s$ 走到 $sdom(y)$ 再沿 $P$ 走到 $y$，最后沿 DFS 树走到 $u$ 的这条路径就不经过 $idom(u)$ 了，这和支配点的定义矛盾。 根据 $idom(u) ≤ sdom(w) < u ≤ w$ 和 $idom(u) < y$ ，唯一的情况就只剩下 $y = idom(u)$ 了， 于是路径 $P$ 包含 $idom(u) $。

上面两个定理说明了半支配点和直接支配点的关系，也给出了由前者求出后者的方法。 对于点 $w \not= s$ 来说，考虑 DFS 树上从 $sdom(w) $ 到 $w$ 的路径上（不包括 $sdom(w)$）的所有点， 令 $u$ 是其中 $sdom$ 最小的点，若 $sdom(u) = sdom(w)$ 则可利用定理 2 得到 $idom(w) = sdom(w)$ ；否则 $u\not=w$ ，可利用定理 3 得到 $idom(w) = idom(u)$ 。

### 2.2 计算半支配点和直接支配点

#### 2.2.1 半支配点

**定理 4**：$sdom(w)$ 由以下两种情况产生的候选取最小值得到。

• 1. 有边 $(v,w)$ ，此时 $v$ 是 $sdom(w)$ 的候选。

• 2. $u$ 是 $v$ 在 DFS 树上的祖先，$u > w$ 且有边 $(v,w)$ ，此时 $sdom(u)$ 是 $sdom(w)$ 的候选。

证明：

•1显然。

•2就取出 $sdom(u)$ 到 $u$ 的半支配点条件中所述的路径，再接上 DFS 树中 $u$ 到 $v$ 的路径，最后从 $v$ 到 $w$ 就是满足 $w$ 的半支配点条件的路径。

然后我们就可以按照 $dfn$ 逆序的顺序来求解 $sdom$ 。

情况1可以直接枚举入边。

情况2可以枚举 $v$ 大于 $w$ 的入边 $(v,w)$ ，向上找大于 $w$ 的祖先，可以使用带权并查集（代码中有实现）。

#### 2.2.2 直接支配点

直接找到 $sdom(w)$ 到 $w$ 中 找到 $sdom$ 最小的值（用 $O(\log n)$ 的做法很容易实现），记为 $u$。

若 $sdom(u) = sdom(w)$ 则可利用定理 2 得到 $idom(w) = sdom(w)$ ；否则 $u\not=w$ ，可利用定理 3 得到 $idom(w) = idom(u)$ 。如此就可以按 $dfn$ 正序求完 $idom$

## 3.应用

### 3.1 某个点集的支配点

点集 $S$ 的支配点定义为 $s$ 到任意一个 $x ∈ S$ 都必须经过的点。不难发现这样的点就是 $S$ 中所有支配点的交集，而点 $x$ 的支配点就是支配树中 $x$ 的所有祖先，因此点集 $S$ 的支配 点就是所有 $x ∈ S$ 在支配树上的最近公共祖先（LCA）。

### 3.2 支配边

对原图的每条边 $(u, v)$ 建立辅助点 $w$ ，并连边 $(u,w)$ 和 $(w, v)$ ，并求出新图的支配树。对于一个原图的节点 $x$ ，它的支配边就是新图的支配树中 $x$ 的是辅助点的祖先。

### 3.3 有向图的割点和桥

**定义**：无向图的割点和桥指删去之后连通分量个数增加的点和边。与之对应地，有向图的强 割点和强桥指删去之后强连通分量个数增加的点和边。

显然有向图的割点和桥都在强连通分量中，因此以下讨论均对**强连通图进行**。

**引理 5.1**：点 $v$ 是强割点当且仅当对于任意 $x \not= v$ 都存在一个点 $y \not= v$ ，使得以下之一成立：

• 1. 任意 $x$ 到 $y$ 的路径都经过 $v$

• 2. 任意 $y$ 到 $x$ 的路径都经过 $v$

边类似。

证明：显然删去这个点后原图不是强连通分量。

于是任选一点 $v$ 即可求出所有除 $v$ 之外的强割点。对于条件 1，只要求出 $DT(G, v)$ ，则支配树中所有除 $v$ 之外的非叶子节点都是强割点；对于条件 2，只要构建出 $G$ 的反图 $G^R$ 并求出 $DT(G^R , v)$ 即可。记得特判你选的点 $v$ ，可以选择重选一点或用 tarjan 判断。

## 4.代码

https://www.luogu.com.cn/problem/P5180

```cpp
#include<bits/stdc++.h>
#define N 200010
using namespace std;
inline int read(){
	static int x=0,f=1;
	x=0,f=1;
	static char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f*=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')x=x*10+int(ch-48),ch=getchar();
	return x;
}
vector<int>v1[N],tree[N],v2[N],e[N];
int fa[N],minn[N],sdom[N],idom[N],siz[N],dfn[N],ek[N],dep[N],vis[N];
int dp[N][21],pos[N][21],w[N][21];
int n,m,cnt;
int find(int x){
	if(!fa[x])return x;
	int f=fa[x];
	fa[x]=find(fa[x]);
	minn[x]=min(minn[x],minn[f]);
	return fa[x];
}
void dfs1(int x,int f){
	vis[x]=1;
	dep[x]=dep[f]+1;
	dfn[x]=++cnt;
	ek[cnt]=x;
	dp[x][0]=f;
	for(int i=1;i<=20;i++)dp[x][i]=dp[dp[x][i-1]][i-1];
	for(int i=0;i<(int)v1[x].size();i++){
		int t=v1[x][i];
		if(t==f||vis[t])continue;
		tree[x].push_back(t);
		dfs1(t,x);
	}
}
void dfs2(int x,int f){
	w[x][0]=dfn[sdom[x]];
	pos[x][0]=x;
	for(int i=1;i<=20;i++){
		if(w[x][i-1]>w[dp[x][i-1]][i-1])pos[x][i]=pos[dp[x][i-1]][i-1];
		else pos[x][i]=pos[x][i-1];
		w[x][i]=min(w[x][i-1],w[dp[x][i-1]][i-1]);
	}
	for(int i=0;i<(int)tree[x].size();i++){
		int t=tree[x][i];
		if(t==f)continue;
		dfs2(t,x);
	}
}
void dfs3(int x,int f){
	siz[x]=1;
	for(int i=0;i<(int)e[x].size();i++){
		int t=e[x][i];
		dfs3(t,x);
		siz[x]+=siz[t];
	}
}
void work1(){
	for(int i=n;i>=2;i--){
		int x=ek[i],res=i;
		for(int j=0;j<(int)v2[x].size();j++){
			int t=v2[x][j];
			if(dfn[t]<dfn[x])res=min(res,dfn[t]);
			else find(t),res=min(res,minn[t]);
		}
		minn[x]=res,sdom[x]=ek[res],fa[x]=dp[x][0];
	}
}
void work2(){
	idom[1]=1;
	for(int i=2;i<=n;i++){
		int x=ek[i],now=x,nowmin=1e9,nowpos=0;
		for(int j=20;j>=0;j--){
			if(dep[dp[now][j]]>=dep[sdom[x]]){
				if(w[now][j]<nowmin)nowpos=pos[now][j],nowmin=w[now][j];
				now=dp[now][j];
			}
		}
		if(nowmin==dfn[sdom[x]])idom[x]=sdom[x];
		else idom[x]=idom[nowpos];
	}
}
int main(){
	memset(w,63,sizeof(w));
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int x=read(),y=read();
		v1[x].push_back(y);
		v2[y].push_back(x);
	}
	dfs1(1,0);
	for(int i=1;i<=n;i++)sdom[i]=minn[i]=dfn[i];
	work1(); 
	dfs2(1,0);
	work2();
	for(int i=2;i<=n;i++)e[idom[i]].push_back(i);
	dfs3(1,0);
	for(int i=1;i<=n;i++)printf("%d ",siz[i]);
}

```

例题:CF757F