2025 5.1 数据结构 最后更新于 2025-05-01 20:17:04

# 5.1 Morning # 数据结构 1.变量->2.数组-> |->**队列**-先进先出 ### 库 ```cpp #include<queue> ``` ### 建队列 ```cpp queue<int> q; //queue-生成了队列 | <int>-是int型的队列 | q-变量名 ``` ### 相关STL ```cpp q.push()//插入元素 q.pop()//删除元素 q.front()//队列头元素 q.size()//队列元素数 ``` ### 当然，爱坐牢的可以手写 ```cpp int a[2333]; int tail=0,head=1; void push(int x) { tail++; a[tail] = x; } void pop() { head++; } int size() { return tail-head+1; } int front() { return a[head]; } ``` #### $Tips$ (高端小坑点) : 不用 ${\color{red} endl {}}$ 用 ${\color{red} "\n" {}}$ (老生常谈了) |->**栈**(桶状的数据结构)-先进后出 ### 库 ```cpp #include<stack> ``` ### 建队列 ```cpp stack<int> s; //stack-生成了队列 | <int>-是int型的队列 | s-变量名 ``` ### 相关STL ```cpp s.push()//插入元素 s.pop()//删除元素 s.size()//栈元素数 ``` ### 手写 ？ “ 没用 ” —zhx ## 单调队列  ### 双端队列调用 & STL ```cpp #include <deque> using namespace std; deque<int> q; //q.push_front() //q.push_front() //q.front() //q.push_back() //q.pop_back() //q.back() ``` ### 手写单调队列 ```cpp const int maxn=1e6; int a[maxn]; void push(int i)//插入下标为i的元素，保证单调递增 { while(q.size() >= 1 && a[q.back()] >= a[i]) q.pop_back; q.push_back(i); } ``` ### 为了解决求最值的题，我们要掏出双指针了 ### 新题   ### 堆 ### 并查集 # Afternoon~  ### another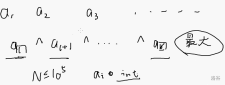：  #### 抑或性质 ： $a\oplus b = b\oplus a$ 以及 $a\oplus a = 0$ #### 引入概念——Trie（字典树） 转二进制，0👈 1👉 **e.g.** $(7)_{10}$ -> $(0111)_2$ 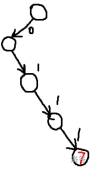 #### $Tips：$ ```cpp int x,y,i; int y=(x>>i)&1 //求x二进制的第i位 ``` ### Damn🐎： ```cpp #include<bits/stdc++.h> using namespace std; struct node{ int nxt[2]; node(){ nxt[0]=nxt[1]=0; } }z[23333]; void insert(int x){ for(int i=30;i>=0;i--){ int y=(x>>i)&1; if(z[p].nxt[y]==0){ cnt++; z[p].nxt[y]=cnt; } p=z[p].nxt[y]; } } int query(int x){ int p=roop,ans=0; for(int i=1;i<=n;i++){ int y=(x>>i)&1; if(z[p].nxt[y^1]!=0)ans=ans|(1<<i),p=z[p].nxt[y^1]; else p=z[p].nxt[y]; } return ans; } ``` ### 于是，又来了可恨的拓展题 #### 题意：求 $$ \sum_{l = 1}^{n} \sum_{r = l}^{n} (a_l \oplus a_{l + 1} \oplus a_{l + 2} \oplus … \oplus a_{r - 1} \oplus a_r) $$ #### 加法与亦或的区别：后者不进位！！！！！ ### 线段树 # 听不懂！！！！