2025 XYD Summer Camp 7.14 模考

## 时间

- 8:30 开 T1 稍微推了推做出来了，过样例之后开始看 T2
- 想了一会儿推了一个计算答案的式子，写完之后发现错了
- 9:00 手模一下发现式子错完了
- 9:40 终于把正确的式子推好了
- 10:00 过了大样例
- T3 联想到一个 trick 秒了，10:30 写完 spj 过了大样例
- 然后一直在做 T4，30 分暴力写完了之后又把特殊性质那一档码完了，可惜最后 10min 没调出来
- 笑点解析：结束前 2min 发现 T1 假了，只能祈祷不要挂太多分

## 成绩

![](https://cdn.luogu.com.cn/upload/image_hosting/p0o2s3ti.png)

## 题解 & 错因

### T1

> 给定一个长度为 $n$ 的序列 $a$，要求构造一个 $01$ 数组 $b$，满足：
> $$
> b_i=\left\{\begin{matrix}0&\text{if }\sum_{j=1}^{i-1}b_i\le a_i\\1&\text{if }\sum_{j=1}^{i-1} b_i=a_i\end{matrix}\right.
> $$
> 求 $\sum_{i=1}^n b_i$ 的最大值。
>
> $1\le n\le 2\times 10^5$，

首先考虑 $b_i=1$ 的位置的 $a_i$ 一定形如 $0,1,2,\cdots$ 这样的序列，因此 $\forall a_i=a_j,i<j$ 只有 $b_j$ 可能为 $1$。在这些可能的位置上贪心填 $1$ 即可。

- 错因：当 $b_i=0$ 的时候直接把限制扔了。

### T2

> 给定 $n,c$，求所有长度为 $n$ 的正整数序列 $a$，满足 $a$ 中所有元素不超过 $c$，且 $a_i$ 是 $a_{i+1}$ 的倍数（也可以相等）。
>
> $1\le n,c\le 5\times 10^7$。

考虑枚举 $a_n$ 即最大的数，先筛出 $5\times 10^7$ 以内的质数，用 dfs 枚举每个质数的次数就可以同时维护出 $a_n$ 质因数分解的结果。现在的限制就是 $\forall i\in [1,n-1]$，$a_i$ 质因数分解后，每个质因子的次数不超过 $a_{i+1}$ 的质因子次数，相当于对于 $a_n$ 的每个质因子的指数，进行 $n-1$ 轮操作，每次减去非负整数，求最后指数非负的方案数，可以用 xtr 寒假讲的一个套路直接用组合数算答案（预处理阶乘逆元后 $O(1)$ 回答）；注意到不同质因子贡献是独立的，整个的答案只要简单乘起来即可。时间复杂度 $O(n+c)$。

```cpp
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0) << "KB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 5e7 + 55, P = 998244353;
const int B = 5e7 + 50;
int n, lim;
int p[maxn >> 2], cnt = 0; bool vis[maxn];
int fac[maxn], inv[maxn];
namespace ModOptions_normal {
    int add(int x, int y) { return (x + y) % P; } void addto(int &x, int y) { (x += y) %= P; }
    int mul(int x, int y) { return 1ll * x * y % P; } void multo(int &x, int y) { x = mul(x, y); }
    int qp(int x, int y) {
        int res = 1; for (; y; y >>= 1, multo(x, x))
            if (y & 1) multo(res, x);
        return res;
    } int divv(int x, int y) { return 1ll * x * qp(y, P - 2) % P; } void divto(int &x, int y) { x = divv(x, y); } 
    int sub(int x, int y) { return (x + P - y) % P; } void subto(int &x, int y) { x = sub(x, y); }
} using namespace ModOptions_normal;
void init() {
    for (int i = 2; i <= 5e7; i ++) {
        if (!vis[i]) p[++ cnt] = i;
        for (int j = 1; 1ll * i * p[j] <= 5e7 && j <= cnt; j ++) {
            vis[i * p[j]] = 1;
            if (i % p[j] == 0) break;
        }
    } fac[0] = inv[0] = 1;
    for (int i = 1; i <= B; i ++) 
        fac[i] = mul(fac[i - 1], i);
    inv[B] = divv(1, fac[B]);
    for (int i = B - 1; i; i --)
        inv[i] = mul(inv[i + 1], i + 1);
} int C(int i, int j) {
    if (i < j) return 0;
    return mul(fac[i], mul(inv[j], inv[i - j]));
} int ans = 0;
void dfs(int now, int pid, int m, int now_ans) {
    if (now > lim) return ;
    addto(ans, now_ans);
    if (pid > cnt) return ;
    for (int nxt_pid = pid; nxt_pid <= cnt; nxt_pid ++) {
        if (1ll * now * p[nxt_pid] > lim) break;
        for (int c = 1, nxt_now = now; ; c ++) {
            if (1ll * nxt_now * p[nxt_pid] > lim) break;
            nxt_now *= p[nxt_pid], dfs(nxt_now, nxt_pid + 1, m + c, mul(now_ans, C(n + c - 1, n - 1)));
        }
    }
}
bool MemoryED; int main() { // open(3);
    cerr << cost_space << '\n';
    scanf("%d %d", &n, &lim), init();
    dfs(1, 1, 1, 1), printf("%d\n", ans);
    return 0;
}
```

### T3

> 给定一张 $n$ 个点 $m$ 条边的无向图，边有边权，求所有 $1$ 到 $n$ 的最短路中最大的边权极差，即对于所有最短路 $p$，求
> $$
> \max_{e\in p}w_e-\min_{e\in p}w_e
> $$
> 的最大值。
>
> $2\le n\le 10^5$，$1\le m\le 2\times 10^5$。保证无重边。

不妨考虑钦定最大值的边 $(u,v)$（首先显然要求这条边在一条最短路上），问题就变成求从 $1$ 到  $u$ 和从 $v$ 到 $n$ 的所有最短路中最小边权的最小值，这个直接正反两遍 dijkstra 即可。接下来貌似还要求 $(u,v)$ 得是这条拼起来的路径上边权最大的边，不过考虑若这条路径是最优解，这条路径上真正的最大边权的边也一定会拿到这条路径里算一次，也就是说 $(u,v)$ 如果不是最大边权的边，那么它的贡献就会被最大边权的边顶掉。所以直接枚举 $(u,v)$ 即可。复杂度 $O(n\log n)$。~~std 好像是线性的，能过就行。~~

```cpp
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5, maxm = 2e5 + 5;
int n, m;
struct Edge { int to, nxt, val; };
struct Graph {
    Edge e[maxm << 1];
    int head[maxn], ecnt = 1;
    void addEdge(int u, int v, int w) { e[++ ecnt] = Edge { v, head[u], w }, head[u] = ecnt; }
} G;
int pre_dis[maxn], pre_mn[maxn], pre[maxn];
bool vis[maxn];
priority_queue<pair<pair<int, int>, int> >q;
void pre_dijkstra() {
    for (int i = 1; i <= n; i ++)
        pre_dis[i] = pre_mn[i] = inf, vis[i] = 0;
    pre_dis[1] = 0, pre_mn[1] = inf, q.push(mk(mk(0, -inf), 1));
    while (!q.empty()) {
        int u = q.top().second; q.pop();
        if (vis[u]) continue; vis[u] = 1;
        for (int i = G.head[u]; i; i = G.e[i].nxt) {
            int v = G.e[i].to, w = G.e[i].val;
            if (pre_dis[v] > pre_dis[u] + 1 || (pre_dis[v] == pre_dis[u] + 1 && pre_mn[v] > min(w, pre_mn[u]))) {
                pre_dis[v] = pre_dis[u] + 1, pre_mn[v] = min(w, pre_mn[u]), pre[v] = u;
                if (!vis[v]) q.push(mk(mk(-pre_dis[v], -pre_mn[v]), v));
            }
        }
    }
}
int suf_dis[maxn], suf_mn[maxn], suf[maxn]; 
void suf_dijkstra() {
    for (int i = 1; i <= n; i ++)
        suf_dis[i] = suf_mn[i] = inf, vis[i] = 0;
    suf_dis[n] = 0, suf_mn[n] = inf, q.push(mk(mk(0, -inf), n));
    while (!q.empty()) {
        int u = q.top().second; q.pop();
        if (vis[u]) continue; vis[u] = 1;
        for (int i = G.head[u]; i; i = G.e[i].nxt) {
            int v = G.e[i].to, w = G.e[i].val;
            if (suf_dis[v] > suf_dis[u] + 1 || (suf_dis[v] == suf_dis[u] + 1 && suf_mn[v] > min(w, suf_mn[u]))) {
                suf_dis[v] = suf_dis[u] + 1, suf_mn[v] = min(w, suf_mn[u]), suf[v] = u;
                if (!vis[v]) q.push(mk(mk(-suf_dis[v], -suf_mn[v]), v));
            }
        }
    }
} void pre_output(int u) {
    if (u == 0) return ;
    pre_output(pre[u]), printf("%d ", u);
} void suf_output(int u) {
    if (u == 0) return ;
    printf("%d ", u), suf_output(suf[u]);
}
bool MemoryED; int main() { // open(2 copy);
    scanf("%d %d", &n, &m);
    for (int i = 1, u, v, w; i <= m; i ++)
        scanf("%d %d %d", &u, &v, &w), G.addEdge(u, v, w), G.addEdge(v, u, w);
    pre_dijkstra(), suf_dijkstra(); int ans = 0, ans_u, ans_v;
    for (int i = 2; i <= G.ecnt; i ++) {
        int u = G.e[i].to, v = G.e[i ^ 1].to;
        if (pre_dis[u] + suf_dis[v] + 1 > pre_dis[n]) continue;
        if (ans <= G.e[i].val - min(min(pre_mn[u], suf_mn[v]), G.e[i].val)) {
            ans = G.e[i].val - min(min(pre_mn[u], suf_mn[v]), G.e[i].val);
            ans_u = u, ans_v = v;
        }
    } printf("%d\n", pre_dis[n]), pre_output(ans_u), suf_output(ans_v);
    return 0;
}
```

### T4

> 给定 $n$ 个点的二叉树，每个点 $u$ 有一个标记 $x_u\in\set{-1,0,1}$；现在会对这棵树进行若干次遍历并生成一个序列 $p$，遍历的方法是：
>
> - 从根节点开始，一开始 $p$ 为空；
> - 假设访问到 $u$，按照其标记分类讨论：
>   - $x_u=-1$，那么先在 $p$ 最后面加上 $u$，然后递归左子树，最后递归右子树。（点 $u$ 进行先序遍历）
>   - $x_u=0$，那么先递归左子树，然后在 $p$ 最后面加上 $u$，最后递归右子树。（点 $u$ 进行中序遍历）
>   - $x_u=1$，那么先递归左子树，然后递归右子树，最后在 $p$ 最后面加上 $u$。（点 $u$ 进行后序遍历）
> - 若递归到空子树直接返回。
>
> $Q$ 次询问，每次询问形如：
>
> - 给定 $[l,r]$ 和一个 $x'$，对于所有 $i\in[l,r]$ 令 $x_i\gets x'$；
> - 对这棵树进行一次遍历，给定点 $u$，求 $u$ 在 $p$ 中的位置。
>
> $1\le n,Q\le 10^5$。

#### Part1 答案咋算

![](https://cdn.luogu.com.cn/upload/image_hosting/q4s8475w.png)

考虑这么一棵树，$u,v$ 分别是 $fa$ 的左儿子和右儿子。考虑 $fa$ 分别进行前序遍历、中序遍历、后序遍历时对于 $u,v$ 的子树的影响。图中中括号的部分即为 $u,v$ 的子树。假设 $fa$ 一开始是中序遍历，那么当 $fa$ 变成前序遍历时，可以发现 $u$ 整颗子树向后挪了一步；当 $fa$ 变成后序遍历的时候，$v$ 整颗子树向前挪了一步。

设 $f(u)$ 表示 $u$ 在 $p$ 中的位置。也就是说，对于 $u$ 的整颗子树 $tr_u$，从**所有祖先都是中序遍历**开始，每有一个祖先 $anc$（包括点 $u$）满足 $anc$ 是**其父亲的左儿子**，并且采用**先序遍历**，那么 $\forall v\in tr_u$，$f(v)$ 的值都会加一；每有一个祖先 $anc$（包括点 $u$）满足 $anc$ 是**其父亲的右儿子**，并且采用**后序遍历**，那么 $\forall v\in tr_u$，$f(v)$ 的值都会减一。也就是说，我们需要对于每个点 $u$ 维护出其祖先中分别满足上述两种条件的祖先的数量，这样就可以简单的根据 $u$ 的标记快速得出 $f(u)$。假设我们得出在**中序遍历下**点 $u$ 的位置是 $f_0(u)$，维护出的 $u$ 的**偏移量**是 $\Delta$；那么 $u$ 进行**中序遍历**的答案就是 $f_0(u)+\Delta$，其他两种情况只需要分别减去左子树大小或加上右子树大小即可。

#### Part2 怎么维护

不妨考虑每个点对其**子树**的贡献。我们设 $tag_1(u)$ 表示 $u$ 有几个祖先 $anc$ 满足 $anc$ 是其父亲的左儿子，并且采用先序遍历；$tag_2(u)$ 表示 $u$ 有几个祖先 $anc$ 是其父亲的右儿子，并且采用后序遍历。对于点 $u$：

- 如果 $u$ 是其父亲 $fa_u$ 的左儿子，且 $x_u=-1$，那么 $u$ 就对 $\forall v\in tr_u$（也包括 $u$）的 $tag_1(u)$ 有 $1$ 的贡献；
- 如果 $u$ 是其父亲 $fa_u$ 的右儿子，且 $x_u=1$，那么 $u$ 就对 $\forall v\in tr_u$（也包括 $u$）的 $tag_2(u)$ 有 $1$ 的贡献。

不妨考虑所有修改的区间长度都为 $1$ 的部分分，那就是对 $tag_1,tag_2$ 中 $u$ 的子树部分进行一个**子树加减**（删掉旧标记的贡献，加上新标记的贡献），询问就是单点查，用差分树状数组维护 dfn 上的区间和即可。扩展到原问题，我们考虑进行**分块**。

- 修改：
  - 对于一个整块，也就是说更新块内的所有点**标记都相同**。不妨维护一个 $cnt_l(k,i)$ 表示对于点 $i$，其祖先（和点 $i$）中有多少个点 $anc$ 在块 $k$ 中且是 $anc$ 的父亲的左儿子；同理维护一个 $cnt_r(k,i)$ 表示 $i$ 祖先中是右儿子且在块 $k$ 内的祖先的个数。那对点 $i$ 的贡献就很好算了，记 $tag_k$ 表示块 $k$ 的标记都是 $tag_k$，那么当 $tag_k=-1$ 时这个块就对任意点 $u$ 有 $cnt_l(k,u)$ 的偏移量贡献；类似当 $tag_k=1$ 时就有 $-cnt_r(k,u)$ 的偏移量贡献。
  - 对于一个散块，直接考虑把整个块原来的信息扬了，暴力把每个点最新的标记求出来，然后每个块整两个树状数组表示**这个块中的点对整棵树的贡献**，按照之前的方法把贡献重新算好即可。
  - 也就是说，当这个块是整块的时候我们看 $cnt_l,cnt_r$ 和 $tag$ 的信息，否则看两个树状数组的信息。
- 查询：按照上面说的枚举每个块查询即可。可能需要特判一下根节点，反正我判了。

这个东西时间复杂度 $O(n\sqrt n\log n)$，luqyou 根据此做法获得了 68pts，前途貌似不是很光明……

#### Part3 优化！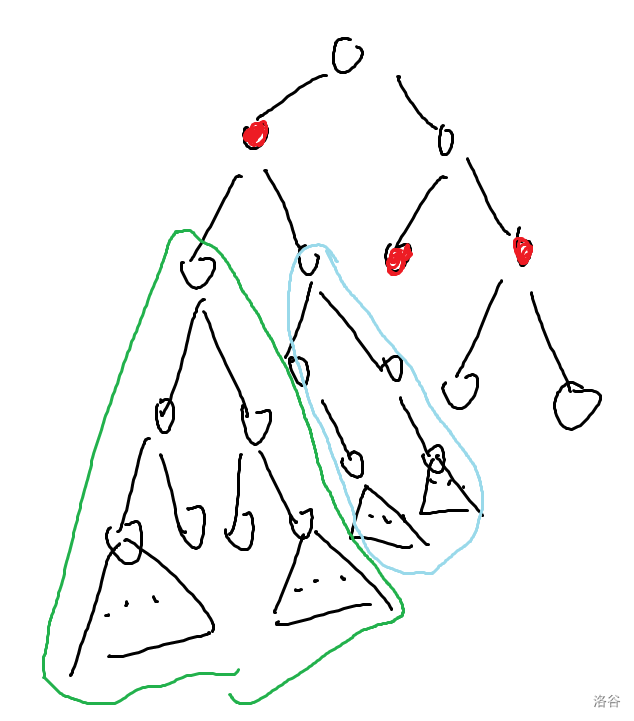

![](https://cdn.luogu.com.cn/upload/image_hosting/ytgl4ubt.png)

考虑这么一棵树，其中红色的点是当前块内的点。考虑这两个分别用绿色和浅蓝色圈起来的两棵子树，可以发现在两个树状数组中，**它们的值是一样的！**也就是说，对于块 $k$ 和一个**块外点** $u$，我们只需要找到 $u$ 中**深度最深的在块里的祖先**（如果没有就说明这个块对 $u$ 没有贡献）$anc$，用 $anc$ 维护的答案再简单根据自己在 $anc$ 的左右子树和 $anc$ 此时的标记做一些微调就得到了 $u$ 的答案！再考虑一个块内点的答案，也是按照其块内祖先的答案加上自己的贡献计算的！

我们不妨把块中的点拿到原树上去建出一个**虚树**，那么树状数组只需维护这个虚树的子树和就可以了；对于块中点直接查树状数组，其他点找到自己在原树的祖先中深度最深的虚树中的点，查这个点的答案并按照上面说的改一改即可。现在时间复杂度优化到了 $O(n\sqrt n\log\sqrt n)$！可是 1000ms 的时限让 under_the_time 感到头疼……

#### Part4 优化！！

这个复杂度还是有点悬。注意到树状数组的操作实际上是在支持我们**动态对块中某个点改标记**，但是本来整个块都被扬了，每个点的新标记也都已经确定，为啥一定要在线呢？我们在虚树上先计算出每个点单独对子树的贡献存在这个点上，然后做个祖先和就可以了！这样时间复杂度 $O(n\sqrt n)$ 足以通过本题……吗？

```cpp
// 在线做法
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5;
int n, Q, f[maxn], son[maxn][2], fa[maxn], clo, siz[maxn]; short x[maxn];
void init_dfs(int u) {
    siz[u] = 1;
    if (son[u][0])
        fa[son[u][0]] = u, init_dfs(son[u][0]), siz[u] += siz[son[u][0]];
    f[u] = ++ clo;
    if (son[u][1])
        fa[son[u][1]] = u, init_dfs(son[u][1]), siz[u] += siz[son[u][1]];
} const int maxm = 205, maxl = 505;
int getway(int u) { return son[fa[u]][1] == u; }
short get_x(int u);
namespace FastIn {
    int read() {
        char c = getchar(); int f = 1;
        for (; c < '0' || c > '9'; c = getchar())
            if (c == '-') f = -f;
        int s = 0;
        for (; c >= '0' && c <= '9'; c = getchar())
            s = (s << 1) + (s << 3) + (c ^ 48);
        return s * f;
    } short sread() {
        char c = getchar(); short f = 1;
        for (; c < '0' || c > '9'; c = getchar())
            if (c == '-') f = -f;
        short s = 0;
        for (; c >= '0' && c <= '9'; c = getchar())
            s = (s << 1) + (s << 3) + (c ^ 48);
        return s * f;
    }
} using namespace FastIn;
struct BLOCK {
    int L, R;
    int id[maxn], vir_cnt;
    int cnt_left[maxn], cnt_right[maxn];
    int tag1[maxl << 1], tag2[maxl << 1];
    int vir_son[maxl << 1][2], vir_fa[maxl << 1];
    int vir_root; pair<int, bool> anc[maxn];
    int real_id[maxl << 1];
    int build(int u, int now_anc, int way) {
        if (u != 1)
            cnt_left[u] = cnt_left[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 0), 
            cnt_right[u] = cnt_right[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 1);
        if (L <= u && u <= R) now_anc = u;
        else anc[u] = mk(now_anc, way);
        int res = 0, l = 0, r = 0;
        if (son[u][0]) l = build(son[u][0], now_anc, now_anc == u ? 0 : way);
        if (son[u][1]) r = build(son[u][1], now_anc, now_anc == u ? 1 : way);
        if (l && r || L <= u && u <= R)  {
            res = id[u] = ++ vir_cnt, real_id[res] = u;
            if (l) vir_fa[l] = res, vir_son[res][0] = l;
            if (r) vir_fa[r] = res, vir_son[res][1] = r;
        } else if (l || r) res = (l | r);
        return res;
    } short tag;
    void update(int u) {
        if (vir_fa[u]) tag1[u] += tag1[vir_fa[u]], tag2[u] += tag2[vir_fa[u]];
        if (vir_son[u][0]) update(vir_son[u][0]);
        if (vir_son[u][1]) update(vir_son[u][1]);
    } void chg_tag(int l, int r, int new_tag) {
        for (int i = L; i <= R; i ++) {
            tag1[id[i]] = tag2[id[i]] = 0;
            if (tag != 2) x[i] = l <= i && i <= r ? new_tag : tag;
            else if (l <= i && i <= r) x[i] = new_tag;
        } tag = 2;
    } int get_virway(int u) {
        return vir_son[vir_fa[u]][1] == u;
    }
    void rebuild() {
        for (int i = L; i <= R; i ++) {
            if (id[i] == vir_root || real_id[vir_fa[id[i]]] < L || real_id[vir_fa[id[i]]] > R) continue;
            if (get_virway(id[i]) == 0 && get_x(real_id[vir_fa[id[i]]]) == -1) tag1[id[i]] = 1;
            if (get_virway(id[i]) == 1 && get_x(real_id[vir_fa[id[i]]]) == 1) tag2[id[i]] = 1;
        } update(vir_root);
    }
} b[maxm]; int bel[maxn];
short get_x(int u) { 
    if (b[bel[u]].tag == 2) return x[u];
    return b[bel[u]].tag;
}
bool MemoryED; int main() { // open(uoj7);
    n = read(), Q = read();
    for (int i = 1; i <= n; i ++)
        son[i][0] = read(), son[i][1] = read(), x[i] = 0;
    init_dfs(1); int m = maxl - 5, k = 1;
    for (int i = 1; i <= n; i += m, k ++) {
        b[k].L = i, b[k].R = min(n, i + m - 1), b[k].vir_cnt = 0;
        for (int j = i; j < i + m && j <= n; j ++)
            bel[j] = k;
        b[k].vir_root = b[k].build(1, 0, 0), b[k].tag = -1;
    } k --; 
    for (int _ = 1, op, l, r, u; _ <= Q; _ ++) {
        op = read();
        if (op == 1) {
            l = read(), r = read(); short new_x = sread();
            if (bel[l] == bel[r]) b[bel[l]].chg_tag(l, r, new_x), b[bel[l]].rebuild();
            else {
                b[bel[l]].chg_tag(l, b[bel[l]].R, new_x), b[bel[r]].chg_tag(b[bel[r]].L, r, new_x);
                for (int i = bel[l] + 1; i < bel[r]; i ++)
                    b[i].tag = new_x;
                b[bel[l]].rebuild(), b[bel[r]].rebuild();
            }
        } else {
            u = read(); short x_u = get_x(u);
            if (u == 1) { printf("%d\n", x_u == -1 ? 1 : x_u == 0 ? f[u] : n); continue; }
            int ans = x_u == -1 ? f[u] - siz[son[u][0]] : x_u == 0 ? f[u] : f[u] + siz[son[u][1]];
            // cout << "pre ans: " << ans << '\n';
            for (int i = 1; i <= k; i ++) {
                // cout << b[i].L << ' ' << b[i].R << ':';
                if (b[i].tag != 2) {
                    ans += (b[i].tag == -1) * b[i].cnt_left[u] - (b[i].tag == 1) * b[i].cnt_right[u];
                    // cout << (b[i].tag == -1) * b[i].cnt_left[u] << ' ' << (b[i].tag == 1) * b[i].cnt_right[u] << '\n';
                } else if (b[i].L <= u && u <= b[i].R) {
                    ans += b[i].tag1[b[i].id[u]] - b[i].tag2[b[i].id[u]];
                    // cout << b[i].tag1[u] << ' ' << b[i].tag2[u] << '\n';
                } else {
                    auto [anc, way] = b[i].anc[u];
                    if (anc == 0) continue;
                    ans += b[i].tag1[b[i].id[anc]] + (way == 0 && get_x(anc) == -1) - (b[i].tag2[b[i].id[anc]] + (way == 1 && get_x(anc) == 1));
                    // cout << b[i].tag1[anc] + (way == 0 && get_x(anc) == -1) << ' ' << (b[i].tag2[anc] + (way == 1 && get_x(anc) == 1)) << '\n';
                }
            } printf("%d\n", ans);
        }
    } cerr << cost_time << '\n';
    return 0;
}
```

![](https://cdn.luogu.com.cn/upload/image_hosting/ppczskeo.png)

#### Part5 优化！！！

实测发现这么做空间复杂度常数爆炸，即使使用 short 也无力通过最后 5 个点。我们考虑把**操作和询问离线下来**，然后**先枚举块再枚举操作和询问**，每次只考虑操作对这个块的影响以及这个块对答案的贡献。其实稍微改改就好了，常数显著优化。

```cpp
// 离线做法
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0) << "KB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5;
int n, Q, f[maxn], son[maxn][2], fa[maxn], clo, siz[maxn]; short x[maxn];
void init_dfs(int u) {
    siz[u] = 1;
    if (son[u][0])
        fa[son[u][0]] = u, init_dfs(son[u][0]), siz[u] += siz[son[u][0]];
    f[u] = ++ clo;
    if (son[u][1])
        fa[son[u][1]] = u, init_dfs(son[u][1]), siz[u] += siz[son[u][1]];
} const int maxm = 205, maxl = 505;
int getway(int u) { return son[fa[u]][1] == u; }
short get_x(int u);
namespace FastIn {
    int read() {
        char c = getchar(); int f = 1;
        for (; c < '0' || c > '9'; c = getchar())
            if (c == '-') f = -f;
        int s = 0;
        for (; c >= '0' && c <= '9'; c = getchar())
            s = (s << 1) + (s << 3) + (c ^ 48);
        return s * f;
    } short sread() {
        char c = getchar(); short f = 1;
        for (; c < '0' || c > '9'; c = getchar())
            if (c == '-') f = -f;
        short s = 0;
        for (; c >= '0' && c <= '9'; c = getchar())
            s = (s << 1) + (s << 3) + (c ^ 48);
        return s * f;
    }
} using namespace FastIn;
struct BLOCK {
    int L, R;
    short id[maxn], vir_cnt; int real_id[maxl << 1];
    short cnt_left[maxn], cnt_right[maxn];
    short tag1[maxl << 1], tag2[maxl << 1];
    short vir_son[maxl << 1][2], vir_fa[maxl << 1];
    short vir_root; pair<int, bool> anc[maxn];
    short build(int u, int now_anc, bool way) {
        if (u != 1)
            cnt_left[u] = cnt_left[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 0), 
            cnt_right[u] = cnt_right[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 1);
        if (L <= u && u <= R) now_anc = u;
        else anc[u] = mk(now_anc, way);
        short res = 0, l = 0, r = 0;
        if (son[u][0]) l = build(son[u][0], now_anc, now_anc == u ? 0 : way);
        if (son[u][1]) r = build(son[u][1], now_anc, now_anc == u ? 1 : way);
        if (l && r || L <= u && u <= R)  {
            res = id[u] = ++ vir_cnt, real_id[res] = u;
            if (l) vir_fa[l] = res, vir_son[res][0] = l;
            if (r) vir_fa[r] = res, vir_son[res][1] = r;
        } else if (l || r) res = (l | r);
        return res;
    } short tag;
    void update(short u) {
        if (vir_fa[u]) tag1[u] += tag1[vir_fa[u]], tag2[u] += tag2[vir_fa[u]];
        if (vir_son[u][0]) update(vir_son[u][0]);
        if (vir_son[u][1]) update(vir_son[u][1]);
    } int get_virway(int u) {
        return vir_son[vir_fa[u]][1] == u;
    }
    void rebuild(int l, int r, short new_tag) {
        for (int i = L; i <= R; i ++) {
            tag1[id[i]] = tag2[id[i]] = 0;
            if (tag != 2) x[i] = l <= i && i <= r ? new_tag : tag;
            else if (l <= i && i <= r) x[i] = new_tag;
        } tag = 2;
        for (int i = L; i <= R; i ++) {
            if (id[i] == vir_root || real_id[vir_fa[id[i]]] < L || real_id[vir_fa[id[i]]] > R) continue;
            if (get_virway(id[i]) == 0 && get_x(real_id[vir_fa[id[i]]]) == -1) tag1[id[i]] ++;
            if (get_virway(id[i]) == 1 && get_x(real_id[vir_fa[id[i]]]) == 1) tag2[id[i]] ++;
        } update(vir_root);
    }
} b; 
// 以上基本不变
short get_x(int u) { 
    if (b.tag == 2) return x[u];
    return b.tag;
} struct Query {
    int op, l, r, u; short new_x;
} que[maxn]; int ans[maxn];
bool MemoryED; int main() { open(uoj13);
    // cerr << cost_space << '\n';
    n = read(), Q = read();
    for (int i = 1; i <= n; i ++)
        son[i][0] = read(), son[i][1] = read(), x[i] = 0;
    for (int i = 1; i <= Q; i ++) {
        auto &[op, l, r, u, new_x] = que[i];
        op = read();
        if (op == 1) l = read(), r = read(), new_x = sread();
        else u = read();
    }
    init_dfs(1); short m = maxl - 5;
    for (int _ = 1; _ <= n; _ += m) {
        for (int i = 1; i <= b.vir_cnt; i ++)
            b.tag1[i] = b.tag2[i] = 0, b.vir_fa[i] = 0, b.vir_son[i][0] = b.vir_son[i][1] = 0;
        for (int i = 1; i <= n; i ++)
            b.anc[i] = mk(0, 0), b.id[i] = b.cnt_left[i] = b.cnt_right[i] = x[i] = 0;
        b.L = _, b.R = min(n, _ + m - 1), b.vir_cnt = b.vir_root = 0;
        b.vir_root = b.build(1, 0, 0), b.tag = -1;
        for (int q = 1; q <= Q; q ++) {
            auto [op, l, r, u, new_x] = que[q];
            if (op == 1) {
                if (l <= b.L && b.R <= r) { b.tag = new_x; continue; }
                if (r < b.L || b.R < l) continue;
                b.rebuild(l, r, new_x);
            } else {
                int &ans = :: ans[q];
                if (u == 1) {
                    if (b.L <= u && u <= b.R) {
                        short x_u = get_x(u);
                        ans += x_u == -1 ? 1 : x_u == 0 ? f[u] : n;
                    } continue;
                } if (b.L <= u && u <= b.R) {
                    short x_u = get_x(u);
                    ans += x_u == -1 ? f[u] - siz[son[u][0]] : x_u == 0 ? f[u] : f[u] + siz[son[u][1]];
                }
                if (b.tag != 2) {
                    ans += (b.tag == -1) * b.cnt_left[u] - (b.tag == 1) * b.cnt_right[u];
                } else if (b.L <= u && u <= b.R) {
                    ans += b.tag1[b.id[u]] - b.tag2[b.id[u]];
                } else {
                    auto [anc, way] = b.anc[u];
                    if (anc == 0) continue;
                    ans += b.tag1[b.id[anc]] + (way == 0 && get_x(anc) == -1) - (b.tag2[b.id[anc]] + (way == 1 && get_x(anc) == 1));
                    // cout << b[i].tag1[anc] + (way == 0 && get_x(anc) == -1) << ' ' << (b[i].tag2[anc] + (way == 1 && get_x(anc) == 1)) << '\n';
                }
            }
        }
    } for (int i = 1; i <= Q; i ++)
        if (que[i].op == 2) printf("%d\n", ans[i]);
    return 0;
}
/*
6 6
2 0
3 0
4 0
5 0
6 0
0 0
2 6
1 2 4 -1
1 1 6 -1
1 2 4 1
1 1 6 -1
2 6
*/
```

#### Part6 一些细节

- 存储虚树相关信息的一些数组都可以开成 short，因为虚树点数一共不超过 short 的范围。
- 块外点存块内点最近的祖先时必须保证**这个祖先在块内**（在虚树上不等于在块上，实际上这个虚树只是用来在重构块信息后**用来统计祖先和的**），而且还要记录它在这个祖先的哪个子树里。
- 当你重构整个块之后、重新计算 $tag_1,tag_2$ 时，应当按照虚树上的结构判断而不是原树结构，也类似的需要判断这对父子是否也都在块中，否则会出现一个点在多个虚树中被统计多次的问题。（参考代码中 rebuild 的部分）xyd 数据太水了导致我一开始写错都能 AC。
- 精细实现！精细实现！精细实现！

正在渲染内容...