数据结构 but not 树局界沟 | 毒瘤题目检测 bot

最后更新于 2025-08-17 08:12:56

作者

LuoFeng_Nanami

分类算法·理论

~~也许这里有一张图，等等就能加载出来了。~~

记录一些典题与妙妙(喵喵) 题。

将会收录特色淮中周赛题！大多数是淮中作业题。

题目下一行是题目的标签。

树状数组部分

树状数组原理+应用（待填坑）

P7527 [USACO21OPEN] United Cows of Farmer John G

树状数组维护种类板子。

考虑以第 $i$ 个数为结尾的满足条件的区间个数。显然这段区间里 $a_i$ 只能出现一次，其一定满足是从前往后枚举时这个数的最后面的位置，或从后往前枚举时这个数最前面的位置。

尝试树状数组维护。由于正常的树状数组维护的是一段前缀，故考虑从后往前枚举。

查询时查询这个数上一个出现的位置以前的满足要求的位置的个数，修改时在树状数组上减去上一个位置，加上这一个位置。

code

F(i, 1, n) { cin >> a[i]; lst[i] = n + 1; }
Fdn(i, n, 1) {
  ans += Query(lst[a[i]] - 1);
  Modify(lst[a[i]], -1);
  lst[a[i]] = i;
  Modify(i, 1);
}
cout << ans;

CF1208D Restore Permutation

树状数组上倍增二分。

手搓样例可以发现最后一个数唯一可以确定，所以考虑从后往前填。具体地使用一个值域树状数组维护前缀和，考虑到第 $i$ 个数，每次二分到一个最大的树状数组内下标 $q$ 使其前缀和等于 $sum_i$，那么位置 $i$ 上的数就是 $q + 1$，最后在树状数组 $q + 1$ 处减去 $q + 1$ 即可。

code

cin >> n;
int logn = log2(n);
F(i, 1, n) { cin >> s[i]; Modify(i, i); }
Fdn(i, n, 1) {
	int p = 0, sum = 0;
	Fdn(j, logn, 0) {
		int np = p + (1 << j);
		if(np <= n && sum + Tree[np] <= s[i]) { sum += Tree[np]; p = np; }
	} 
    ans[i] = p + 1; Modify(p + 1, -p - 1);
}
F(i, 1, n) cout << ans[i] << ' ';

线段树部分

P8955 P4269 P4198 P8904

P7706 「Wdsr-2.7」文文的摄影布置

我不会同时维护 $i,j,k$！那咋办？分开来维护呗！

这类线段树题的核心，首先是考虑合并两个区间信息的操作。大区间的答案可以有三种方法得到：

直接从两个小区间上传；
左边小区间 $a_i$ 的最大值加上右边小区间 $-b_j+a_k(j<k)$ 的最大值；
左边小区间 $a_i-b_j(i<j)$ 的最大值加上右边小区间 $a_k$ 的最大值。

所以，对于线段树上的每个节点，我们只需要维护 5 个信息：区间 $a$ 最大值，$b$ 最小值，$a_i-b_j(i<j)$ 最大值，$-b_j+a_k(j<k)$ 最大值，区间答案。

区间 $a_i-b_j(i<j)$ 最大值、$-b_j+a_k(j<k)$ 最大值合并考虑方式同理。

其次，对于这类线段树题，我们还要着重考虑修改操作。但这题修改操作平凡，直接改就行。较为繁琐的修改见下一题。

code

const int maxn = 5e5 + 7;

int n, m;
int a[maxn], b[maxn];

struct tree {
	int amax, bmin, lmax, rmax, ans;

	tree operator + (const tree &x) const {
		tree ret;
		ret.amax = max(amax, x.amax); ret.bmin = min(bmin, x.bmin);
		ret.lmax = max(max(lmax, x.lmax), amax - x.bmin);
		ret.rmax = max(max(rmax, x.rmax), x.amax - bmin);
		ret.ans = max(max(ans, x.ans), max(lmax + x.amax, amax + x.rmax));
		return ret;
	}
} Tree[maxn << 2];

inline void PushUp(int p) { Tree[p] = Tree[p << 1] + Tree[p << 1 | 1]; }

inline void Build(int p, int l, int r) {
	if(l == r) return Tree[p] = {a[l], b[l], -inf, -inf, -inf}, void();
	int mid = (l + r) >> 1;
	Build(p << 1, l, mid), Build(p << 1 | 1, mid + 1, r);
	PushUp(p);
}

inline void Modify(int p, int l, int r, int k, int op) {
	if(l == r) return (op ? Tree[p].amax = a[k] : Tree[p].bmin = b[k]), void();
	int mid = (l + r) >> 1;
	if(k <= mid) Modify(p << 1, l, mid, k, op);
	else Modify(p << 1 | 1, mid + 1, r, k, op);
	PushUp(p);
}

inline tree Query(int p, int l, int r, int s, int t) {
	if(s <= l && r <= t) return Tree[p];
	int mid = (l + r) >> 1;
	if(s <= mid && mid < t) return Query(p << 1, l, mid, s, t) + Query(p << 1 | 1, mid + 1, r, s, t);
	if(s <= mid) return Query(p << 1, l, mid, s, t);
	if(mid < t) return Query(p << 1 | 1, mid + 1, r, s, t);
}


signed main() {
//	freopen("saki.in", "r", stdin);
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n >> m;
	F(i, 1, n) cin >> a[i]; F(i, 1, n) cin >> b[i];
	Build(1, 1, n);
	F(i, 1, m) {
		int op, x, y, l, r; cin >> op;
		if(op == 1) {
			cin >> x >> y;
			a[x] = y; Modify(1, 1, n, x, 1);
		} else if(op == 2) {
			cin >> x >> y;
			b[x] = y; Modify(1, 1, n, x, 0);
		} else {
			cin >> l >> r;
			cout << Query(1, 1, n, l, r).ans << '\n';
		}
	}
	

    return 0;
}

CF1690G Count the Trains

本题有 $3$ 种做法，这个部分仅介绍线段树做法，另外的做法分别在 set 和珂朵莉树部分。

手搓题意可知题目中求不同前缀 min 个数，一个重要的性质是前缀 min 不增，所以一定是一段一段变小的形式，于是我们用线段树维护前缀 min，即 $b_i$。

继续考虑如何合并两个区间信息。我们发现如果左区间最右一段和右区间最左一段存的数相同，则总段数是两个区间段数和减一，否则就是两个区间段数和。

难点来了：考虑如何修改。打开草稿本，画 $b_i$ 的图理解一下！我们发现如果修改后的 $a_k$ 小于原来的 $b_k$，则意味着下面一段的 $b$ 都要变小。具体地，我们在线段树上二分到最前面的 $q$，使 $b_q \leq$ 修改过后的 $b_k$，然后 $k \sim q-1$ 的 $b$ 都要修改为改过的 $b_k$。

code

const int maxn = 1e5 + 7;
 
int _;
int n, m;
int a[maxn], smin[maxn];
 
struct tree {
	int tmin, lmin, rmin, cnt, Lazy;
 
	tree operator + (const tree &x) const {
		tree ret;
		ret.tmin = min(tmin, x.tmin);
		ret.lmin = lmin, ret.rmin = x.rmin;
		ret.cnt = cnt + x.cnt - (rmin == x.lmin);
		return ret;
	}
} Tree[maxn << 2];
 
inline void PushUp(int p) { int tag = Tree[p].Lazy; Tree[p] = Tree[p << 1] + Tree[p << 1 | 1]; Tree[p].Lazy = tag; }
 
inline void PushDown(int p) {
	if(Tree[p].Lazy == -inf) return ;
	Tree[p << 1].tmin = Tree[p << 1].lmin = Tree[p << 1].rmin = Tree[p << 1].Lazy = Tree[p].Lazy;
	Tree[p << 1].tmin = Tree[p << 1 | 1].lmin = Tree[p << 1 | 1].rmin = Tree[p << 1 | 1].Lazy = Tree[p].Lazy;
	Tree[p << 1].cnt = Tree[p << 1 | 1].cnt = 1;
	Tree[p].Lazy = -inf;
}
 
inline void Build(int p, int l, int r) {
	Tree[p].Lazy = -inf;
	if(l == r) return Tree[p].tmin = Tree[p].lmin = Tree[p].rmin = smin[l], Tree[p].cnt = 1, void();
	int mid = (l + r) >> 1;
	Build(p << 1, l, mid), Build(p << 1 | 1, mid + 1, r);
	PushUp(p);
}
 
inline void Modify(int p, int l, int r, int s, int t, int v) {
	if(s <= l && r <= t) {
		Tree[p].tmin = Tree[p].lmin = Tree[p].rmin = Tree[p].Lazy = v;
		Tree[p].cnt = 1;
		return ;
	}
	int mid = (l + r) >> 1;
	PushDown(p);
	if(s <= mid) Modify(p << 1, l, mid, s, t, v);
	if(mid < t) Modify(p << 1 | 1, mid + 1, r, s, t, v);
	PushUp(p);
}
 
inline int Query(int p, int l, int r, int s, int t) {
	if(s <= l && r <= t) return Tree[p].tmin;
	int mid = (l + r) >> 1, ret = inf;
	PushDown(p);
	if(s <= mid) ret = min(ret, Query(p << 1, l, mid, s, t));
	if(mid < t) ret = min(ret, Query(p << 1 | 1, mid + 1, r, s, t));
	return ret;
}
 
inline int B_Query(int p, int l, int r, int v) {
	if(Tree[p].tmin > v) return r + 1;
	if(l == r) return l;
	int mid = (l + r) >> 1;
	PushDown(p);
	if(Tree[p << 1].tmin > v) return B_Query(p << 1 | 1, mid + 1, r, v);
	else return B_Query(p << 1, l, mid, v);
}
 
signed main() {
//	freopen("saki.in", "r", stdin);
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
 
	cin >> _;
	smin[0] = inf;
	while(_--) {
		cin >> n >> m;
		F(i, 1, n) { cin >> a[i]; smin[i] = min(smin[i - 1], a[i]); }
		Build(1, 1, n);
		F(i, 1, m) {
			int k, d; cin >> k >> d;
			a[k] -= d; int tmp = (k == 1 ? a[k] : min(a[k], Query(1, 1, n, 1, k - 1)));
			int pos = B_Query(1, 1, n, tmp) - 1;
			if(pos >= k) Modify(1, 1, n, k, pos, tmp);
			cout << Tree[1].cnt << " ";
		}
		cout << '\n';
	}
	
 
    return 0;
}

权值线段树

可持久化线段树

两维：时间线，下标
时间线：满足可减性/或/没有下界或上界限制
二维数点理解：可减或有一个方向没有限制
拓展：维护树上路径（差分）

P9388 [THUPC 2023 决赛] 先人类的人类选别

抱抱卧真堂。

容易发现，对于一个区间，一次操作之后，一定有 $x$ 本身或者是区间最小值被带走。那么 $m$ 次操作后，留下的一定是 $x_1 \sim x_m$ 和 $a_l \sim a_r$ 中的前 $r - l + 1$ 大数。

考虑差分，用可持久化线段树维护区间和与修改的 $x$，每次询问就是 $[1, r]$ 的答案减去 $[1, l - 1]$ 的答案。查询时在两棵树上同时二分即可。

code

const int maxn = 5e5 + 7;

int n, m;
int a[maxn], R[maxn];

struct tree {
	int ls, rs, siz;
    ll sum;
} Tree[maxn * 50];
int tot;

inline void Modify(int &p, int q, int l, int r, int k) {
	Tree[p = ++tot] = {Tree[q].ls, Tree[q].rs, Tree[q].siz + 1, Tree[q].sum + k};
	if(l == r) return ;
	int mid = (l + r) >> 1;
	if(k <= mid) Modify(Tree[p].ls, Tree[q].ls, l, mid, k);
	else Modify(Tree[p].rs, Tree[q].rs, mid + 1, r, k);
}

inline ll Query(int p, int q, int l, int r, int k) {
	if(l == r) return k * l; // 注意特殊的返回值
	int mid = (l + r) >> 1, ret = Tree[Tree[p].rs].siz + Tree[Tree[q].rs].siz;
	if(k <= ret) return Query(Tree[p].rs, Tree[q].rs, mid + 1, r, k);
	else return Query(Tree[p].ls, Tree[q].ls, l, mid, k - ret) + Tree[Tree[p].rs].sum + Tree[Tree[q].rs].sum;
}


signed main() {
//	freopen("saki.in", "r", stdin);
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n >> m;
	F(i, 1, n) { cin >> a[i]; Modify(R[i], R[i - 1], 1, n, a[i]); }
	int exR = 0;
	F(i, 1, m) {
		int x, l, r; cin >> x >> l >> r;
		Modify(exR, exR, 1, n, x);
		cout << Query(R[r], exR, 1, n, r) - Query(R[l - 1], exR, 1, n, l - 1) << '\n';
	}
	

    return 0;
}

Trie

咕咕咕。

01Trie

01Trie，顾名思义，就是边权只有 $0$ 和 $1$ 两种的 Trie 树，因为它很好地满足了一般处理异或问题的“拆位思想”，所以一般被用于异或有关的问题。

一般来说，01Trie 有两种构造方式：从低位到高位插入与从高位到低位插入。从低位到高位插入，使得它能够很快地处理修改操作，一般用于带修的题目；从高位到低位插入，使得它具有一些良好的性质，例如满足贪心的最优策略等等，一般用于处理各种形式的异或最值。

在代码实现上，既有一目了然的数组实现，也有短小精悍的指针实现，大家可以都学习一下。

下面，我将列出一些 01Trie 的典型例题，探讨 01Trie 的具体应用。

P10471 最大异或对 The XOR Largest Pair

考虑将所有数从高位到低位插入到 01Trie 中，每次枚举一个数，找到它在 Trie 上与它异或和最大的答案，与总答案取最大值即可。

具体地，我们枚举这个数的每一位，同时尽可能找不一样的数位往低位走。容易证明，这样一定是最大的。时间复杂度 $O(n \log V)$，其中 $V$ 是值域。

code

F(i, 1, n) {
    int u = 1, c;
    F(j, 1, 31) {
        c = (a[i] >> (31 - j)) & 1;
        if(!ch[u][c]) ch[u][c] = ++tot;
        u = ch[u][c];
    }
}
F(i, 1, n) {
    int u = 1, v = 1, ret = 0, c;
    F(j, 1, 31) {
        c = (a[i] >> (31 - j)) & 1;
            if(ch[u][c] && ch[v][!c]) {
            ret += (1 << (31 - j));
            u = ch[u][c], v = ch[v][!c];
        } else u = ch[u][c], v = ch[v][c];
    }
    ans = max(ret, ans);
} cout << ans;

P4551 最长异或路径

考虑维护每个点到根的路径的异或和 $a_i$。可以证明，两点 $u,v$ 间异或路径的长度为 $a_u \oplus a_v$。这样，我们就把它转换成了上个问题。这里不再给出实现。

P8511 [Ynoi Easy Round 2021] TEST_68

先考虑暴力解法。dfs，每个点记录 Trie 状态，跑上面 P10471 的查询，传下去，然后回溯。这样时间复杂度是 $O(n^2 \log V)$ 的，无法接受。

观察到最后，有很多点的答案都是一样的，我们可以考虑先求出任意一对权值异或和最大的点 $u, v$，进行讨论。如果它不在 $u$ 或 $v$ 到根

平衡树

咕咕咕。

CF702F T-Shirts

首先分析题意：用每个物品按 $q$ 从大到小来找买的人，如果这人 $b \ge c$ 答案加一。

我们有一个基于暴力的势能分析 2log 做法和一个基于 dp 的 1log 可持久化平衡树做法。

宝宝，我不会可持久化平衡树怎么办，2log 能卡过去吗？

可以的！首先给每个物品按 $q$ 从大到小排序，以每个人为节点建一棵平衡树。那么我们枚举物品 $i$，我们发现这时人有 $3$ 种，$j$ 表示第 $j$ 个人：

$b_j \in [0,c_i)$，买不起的；
$b_j \in [c_i, 2c_i)$ 买得起，买完后就会和上一种人有交；
$b_j \in [2c_i, +\infty)$ 也买得起，但买完后和上面的人无交。

所以呢？所以我们把平衡树按上面的分类分成三棵，之后第二种人暴力修改插入第一种人的树，第三种人直接打 lazytag 就行。

注意到暴力改过的数最后都会变成自己的一半以下，所以每个数最多被改 log 次，所以复杂度是 $O(n \log n \log V)$。

code

const int maxn = 2e5 + 7;

int n, m;
struct obj { int c, q; bool operator < (const obj &x) const { return (q == x.q ? q > x.q : c < x.c); } } a[maxn];

int val[maxn], ls[maxn], rs[maxn], cnt[maxn], id[maxn], Lazyd[maxn], Lazyc[maxn], rd[maxn], tot, R;
int ans[maxn];

inline int N(int v, int i) { int x = ++tot; val[x] = v, id[x] = i, rd[i] = rnd(); return x; }

inline void PushDown(int p) {
	if(Lazyc[p]) {
		if(ls[p]) Lazyc[ls[p]] += Lazyc[p], cnt[ls[p]] += Lazyc[p];
		if(rs[p]) Lazyc[rs[p]] += Lazyc[p], cnt[rs[p]] += Lazyc[p];
		Lazyc[p] = 0;
	} 
	if(Lazyd[p]) {
		if(ls[p]) Lazyd[ls[p]] += Lazyd[p], val[ls[p]] -= Lazyd[p];
		if(rs[p]) Lazyd[rs[p]] += Lazyd[p], val[rs[p]] -= Lazyd[p];
		Lazyd[p] = 0;
	}
}

inline void Split(int p, int v, int &x, int &y) {
	if(!p) return x = y = 0, void();
	PushDown(p);
	if(val[p] <= v) return Split(rs[p], v, rs[x = p], y), void();
	return Split(ls[p], v, x, ls[y = p]), void();
}

inline int Merge(int x, int y) {
	if(!x | !y) return x | y;
	PushDown(x), PushDown(y);
	if(rd[x] < rd[y]) return ls[y] = Merge(x, ls[y]), y;
	return rs[x] = Merge(rs[x], y), x;
}

inline void Insert(int v, int i) {
	int x, y; Split(R, v - 1, x, y);
	R = Merge(Merge(x, N(v, i)), y);
}

inline void dfs1(int p, int &exR, int del) {
	if(!p) return ;
	PushDown(p);
	if(ls[p]) dfs1(ls[p], exR, del);
	if(rs[p]) dfs1(rs[p], exR, del);
	ls[p] = rs[p] = 0; val[p] -= del, cnt[p]++;
	int x, y; Split(exR, val[p] - 1, x, y);
	exR = Merge(Merge(x, p), y);

}

inline void dfs2(int p) {
	if(!p) return ;
	PushDown(p);
	if(ls[p]) dfs2(ls[p]);
	if(rs[p]) dfs2(rs[p]);
	ans[id[p]] = cnt[p];
}

signed main() {
//	freopen("saki.in", "r", stdin);
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n;
	F(i, 1, n) cin >> a[i].c >> a[i].q;
	sort(a + 1, a + 1 + n);
	cin >> m;
	F(i, 1, m) {
		int v; cin >> v;
		Insert(v, i);
	}
	F(i, 1, n) {
		int x, y, z; Split(R, a[i].c - 1, x, y); Split(y, (a[i].c << 1) - 1, y, z);
		if(z) {
			val[z] -= a[i].c, cnt[z]++;
			Lazyc[z]++, Lazyd[z] += a[i].c;
		}
		if(y) dfs1(y, x, a[i].c);
		R = Merge(x, z);
	}
	dfs2(R);
	F(i, 1, m) cout << ans[i] << " ";

	

    return 0;
}

可持久化平衡树

STL set

P6617 查找 Search

这题啊，naive！

强制在线所以不能莫队呜呜呜。

记 $i$ 后面最近的一个 $w - a_i$ 位置为 $\text{nxt}_i$，使用线段树维护。那么查询就变成了：在 $l$ 及之后，有没有 $\text{nxt}_i \leq r$ 的。

因为 $w$ 是确定的，值域又只有 $5 \times 10^5$，我们可以把值为 $v$ 和 $w - v$ 的位置放进一个 set 里维护。

观察下图我们可以发现，在同一个 set 中，相邻的数产生的 $\text{nxt}$ 才是有意义的！如果两个相邻的数的值 $a_i, a_j$ 相等，那么 $\text{nxt}_i = \text{nxt}_j$，所以前面的那个数就是废物，不管怎样都会对统计产生重复的贡献！具体地，如果我们想让它产生贡献，那么 $l \leq i, \text{nxt}_i \leq r$，显然满足 $l \leq j, \text{nxt}_j \leq r$，还不如让 $j$ 来。

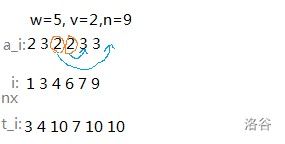
然后我们发现，对于每次修改，最多只有 $3$ 个地方的 $\text{nxt}$ 值会被修改：

$\min(a_{pos}, w - a_{pos})$ 这个 set 中小于 $pos$ 的第一个位置；
插入新 set 后，$pos$ 自身；
新 set 中，小于 $pos$ 的第一个位置；

然后就结束辣！

code

const int maxn = 5e5 + 7;

int n, m, w;
set<int> S[maxn >> 1];
int a[maxn], nxt[maxn];
int Tree[maxn << 2];

inline void PushUp(int p) { Tree[p] = min(Tree[p << 1], Tree[p << 1 | 1]); }

inline void Build(int p, int l, int r) {
	if(l == r) return Tree[p] = nxt[l], void();
	int mid = (l + r) >> 1;
	Build(p << 1, l, mid), Build(p << 1 | 1, mid + 1, r);
	PushUp(p);
} 

inline void Modify(int p, int l, int r, int k, int v) {
	if(l == r) return Tree[p] = v, void();
	int mid = (l + r) >> 1;
	if(k <= mid) Modify(p << 1, l, mid, k, v);
	else Modify(p << 1 | 1, mid + 1, r, k, v);
	PushUp(p);
}

inline int Query(int p, int l, int r, int s, int t) {
	if(s <= l && r <= t) return Tree[p];
	int mid = (l + r) >> 1, ret = inf;
	if(s <= mid) ret = min(ret, Query(p << 1, l, mid, s, t));
	if(mid < t) ret = min(ret, Query(p << 1 | 1, mid + 1, r, s, t));
	return ret;
}

signed main() {
//	freopen("saki.in", "r", stdin); 
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	
    cin >> n >> m >> w;
    F(i, 0, w >> 1) S[i].insert(n + 1);
    a[0] = -inf;
    F(i, 1, n) { cin >> a[i]; S[min(a[i], w - a[i])].insert(i); }
    F(i, 1, n) {
		auto it = ++S[min(a[i], w - a[i])].lower_bound(i);
		nxt[i] = (a[i] != a[*it] ? *it : n + 1); 
	}
	Build(1, 1, n);
	int cnt = 0;
	F(i, 1, m) {
		int op, pos, val, l, r; cin >> op;
		if(op == 1) {
			cin >> pos >> val;
			int q1 = min(a[pos], w - a[pos]), q2 = min(val, w - val);
			S[q1].erase(pos);
			auto it = S[q1].lower_bound(pos);
			if(it != S[q1].begin()) {
				int tmp = *it; 
				it--;
				nxt[*it] = (a[tmp] != a[*it] ? tmp : n + 1);
				Modify(1, 1, n, *it, nxt[*it]);
			}
			a[pos] = val;
			S[q2].insert(pos);
			it = S[q2].lower_bound(pos);
			it++;
			nxt[pos] = (a[pos] != a[*it] ? *it : n + 1);
			Modify(1, 1, n, pos, nxt[pos]);
			it--; 
			if(it != S[q2].begin()) {
				it--;
				nxt[*it] = (a[pos] != a[*it] ? pos : n + 1);
				Modify(1, 1, n, *it, nxt[*it]);
			}
		} else {
			cin >> l >> r; l ^= cnt, r ^= cnt;
			bool fl = (Query(1, 1, n, l, n) <= r);
			cout << (fl ? "Yes\n" : "No\n"); cnt += fl;
		}
	}
    
    
	return 0;
}

珂朵莉树（ODT、颜色段均摊）

P4690 [Ynoi Easy Round 2016] 镜中的昆虫

省选前调了 inf 天，也是无敌了！

咕咕咕

code

const int maxn = 2e5 + 7, maxm = 1.5e6 + 7;

int n, m;
int a[maxn], lst[maxn], pre[maxn];
map<int, int> Mp, num;
int tot, rnk[maxn];

struct Ctl {
    mutable int l, r, v;
    bool operator < (const Ctl &x) const { return l < x.l; }
};
set<Ctl> CT, S[maxn];

struct cdq {
    int x, y, v, ti, id;
} Q[maxm];
int cnt;
int ans[maxn], qwq;

int Tree[maxn];
inline int lowbit(int x) { return (x & (-x)); }
inline void Add(int x, int v) { ++x; for(; x < maxn; x += lowbit(x)) Tree[x] += v; }
inline int Query(int x) { ++x; int ret = 0; for(; x; x -= lowbit(x)) ret += Tree[x]; return ret; }

inline int Get(int x) {
    auto It = CT.upper_bound({x, 0, 0}); It--;
    if(It -> l < x) return x - 1;
    auto _It = S[num[It -> v]].lower_bound({x, 0, 0});
    if(_It != S[num[It -> v]].begin()) { _It--; return _It -> r; }
    return 0;
}

inline void AddQ(int x, int ti) {
    Q[++cnt] = {x, pre[x], -1, ti, 0};
    pre[x] = Get(x);
    Q[++cnt] = {x, pre[x], 1, ti, 0};
}

inline auto Split(int x) {
    auto It = CT.lower_bound({x, 0, 0});
    if(It != CT.end() && It -> l == x) return It;
    It--;
    int l = It -> l, r = It -> r, v = It -> v;
    CT.erase(It); S[num[v]].erase(*It);
    CT.insert({l, x - 1, v}); S[num[v]].insert({l, x - 1, v});
    S[num[v]].insert({x, r, v});
    return CT.insert({x, r, v}).fi;
}

inline void Modify(int l, int r, int v, int ti) {
    if(!num[v]) { num[v] = ++tot; rnk[tot] = v; }
    auto It2 = Split(r + 1); auto It1 = Split(l);
    vector<int> vec;
    for(auto It = It1; It != It2; It++) {
        vec.push_back(It -> l);
        auto _It = S[num[It -> v]].upper_bound(*It);
        if(_It != S[num[It -> v]].end()) vec.push_back(_It -> l);
        S[num[It -> v]].erase(*It);
    }
    CT.erase(It1, It2);
    CT.insert({l, r, v});
    S[num[v]].insert({l, r, v});
    auto _It = S[num[v]].upper_bound({l, r, v});
    if(_It != S[num[v]].end()) vec.push_back(_It -> l);
    for(int i : vec) AddQ(i, ti);
}

inline void CDQ(int l, int r) {
    if(l == r) return ;
    int mid = (l + r) >> 1;
    CDQ(l, mid), CDQ(mid + 1, r);
    int i = l;
    F(j, mid + 1, r) {
        while(i <= mid && Q[i].x <= Q[j].x) {
            if(!Q[i].id) Add(Q[i].y, Q[i].v);
            i++;
        }
        if(Q[j].id) ans[Q[j].id] += Query(Q[j].y) * Q[j].v;
    }
    F(k, l, i - 1) if(!Q[k].id) Add(Q[k].y, -Q[k].v);
    inplace_merge(Q + l, Q + mid + 1, Q + r + 1, [] (const cdq &p, const cdq &q) { return (p.x == q.x ? p.id < q.id : p.x < q.x); } );
}

signed main() {
//	freopen("saki.in", "r", stdin);
//	freopen("saki.out", "w", stdout);
	
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	
    cin >> n >> m;
    F(i, 1, n) {
        cin >> a[i];
        pre[i] = Mp[a[i]];
        Mp[a[i]] = i;
        if(!num[a[i]]) { num[a[i]] = ++tot; rnk[tot] = a[i]; }
        Q[++cnt] = {i, pre[i], 1, 0, 0};
    } int lst = 0;
    F(i, 1, n + 1) {
        if(a[i] != a[i - 1]) {
            CT.insert({lst, i - 1, a[i - 1]});
            S[num[a[i - 1]]].insert({lst, i - 1, a[i - 1]});
            lst = i;
        }
    }
    auto It = CT.lower_bound({0, 0, 0}); CT.erase(It);
    F(i, 1, m) {
        int op, l, r, x; cin >> op >> l >> r;
        if(op == 1) {
            cin >> x;
            Modify(l, r, x, i);
        } else {
            Q[++cnt] = {l - 1, l - 1, -1, i, ++qwq};
            Q[++cnt] = {r, l - 1, 1, i, qwq};
        }
    }
    sort(Q + 1, Q + cnt + 1, [] (const cdq &x, const cdq &y) { return (x.ti == y.ti ? x.id < y.id : x.ti < y.ti); });
    CDQ(1, cnt);
    F(i, 1, qwq) cout << ans[i] << '\n';

    
	return 0;
}

数据结构 but not 树局界沟 | 毒瘤题目检测 bot

树状数组部分

P6225 [eJOI2019] 异或橙子

P3372 【模板】线段树 1

P7527 [USACO21OPEN] United Cows of Farmer John G

P6619 [省选联考 2020 A/B 卷] 冰火战士

CF1208D Restore Permutation

线段树部分

P7706 「Wdsr-2.7」文文的摄影布置

CF1690G Count the Trains

CF1149C Tree Generator™

权值线段树

可持久化线段树

P9388 [THUPC 2023 决赛] 先人类的人类选别

Trie

01Trie

P10471 最大异或对 The XOR Largest Pair

P4551 最长异或路径

P6018 [Ynoi2010] Fusion tree

P8511 [Ynoi Easy Round 2021] TEST_68

P6072 『MdOI R1』Path

P6623 [省选联考 2020 A 卷] 树

平衡树

CF702F T-Shirts

可持久化平衡树

CF702F T-Shirts

STL set

P6617 查找 Search

珂朵莉树（ODT、颜色段均摊）

P4690 [Ynoi Easy Round 2016] 镜中的昆虫

分块

莫队