地↘批↗酱~
标题的意思是模仿教练读 DP 的口音。
斜率优化
模型讲解
一般可以斜率优化的转移方程长这样: $$ f_i = \min 或 \max_{j=0}^{i-1}{h_j+v_jw_i+g_i} $$ 我们注意到 g_i 可以移到外面,所以实际上这个式子就是: $$ \min 或 \max_{j=0}^{i-1}{h_j+v_jw_i}+g_i $$ 注意到大括号内可以看做关于 $w_i$ 的一次函数 $y=kx+b$ 的形式,于是我们有第一种斜率优化方式:
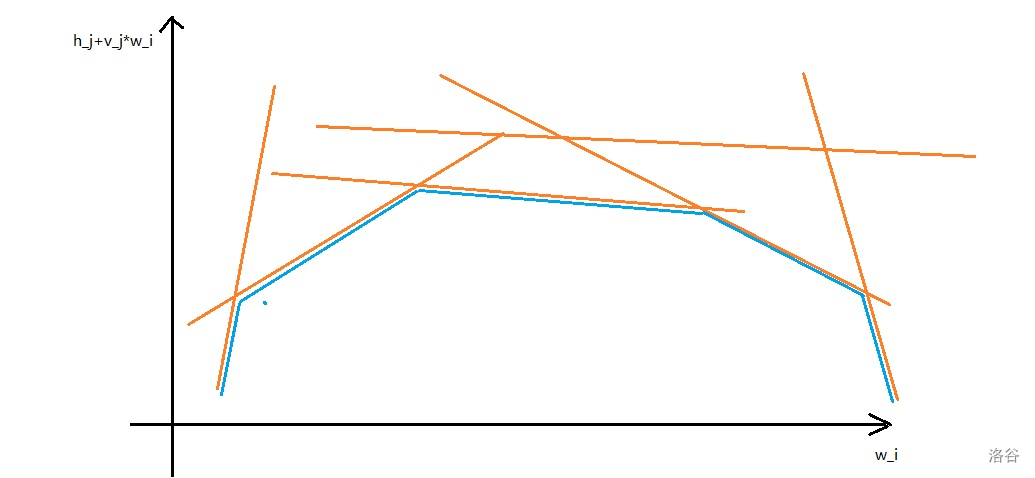
如图所示,橙线为不同的 $j$ 所表示的一次函数,蓝色为取的最小值。李超线段树维护即可。
如果 $v_j$ 具有单调性,我们还有第二种优化方式:
我们将每一个 $j$ 表示成坐标系上的一点 $(-v_j, h_j)$,让斜率为 $w_i$ 的直线过这个点,那么它与 $y$ 轴的交点就是 $h_j+v_jw_i$。
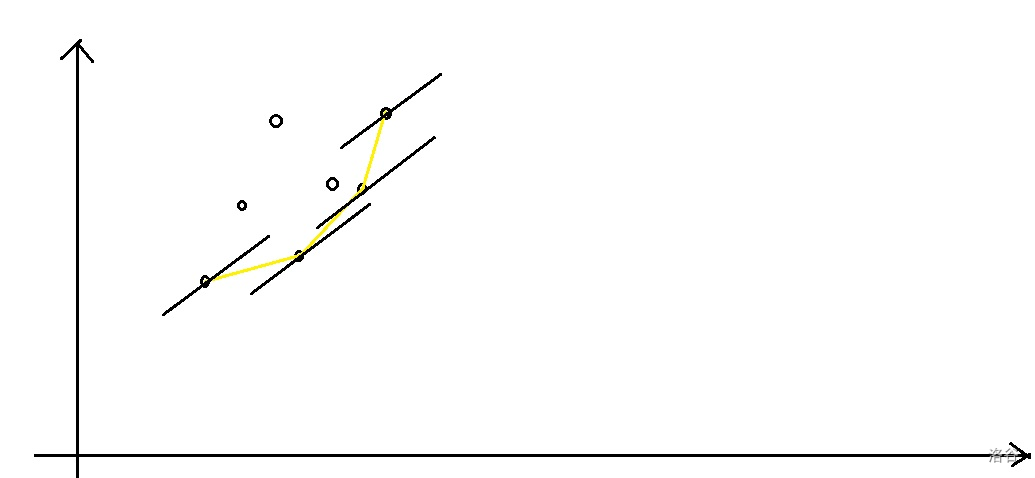
如图所示,我们维护一个凸包,然后用斜率为 $w_i$ 的直线去切这个凸包。
一般地,若 $-v_j$ 递减,我们可以通过调整 $-v_j$ 和 $w_i$ 的正负号,使 $-v_j$ 递增。
下面我们仅考虑最小值,最大值同理可以得到做法。具体可分为以下两种情况:
- $w_i$ 递增:用单调队列维护下凸包,队头斜率若小于 $w_i$ 则出队,一般不考虑等于的情况,对于每个 $i$ 取对应时刻的队头即为最优决策点。
- $w_i$ 不递增(递减或无序):用单调队列维护下凸包,请注意,这时不需要弹出队头。在单调队列上二分斜率即可。
对于 $v_j$ 不具有单调性的情况,用其他方法一般不如第一种李超线段树直接。
例题
记 $s_i$ 为第 $i$ 段的和,首先我们有方差的另一个表示方式: $$ v=(\sum_{i=1}^m \frac{s_i^2}{m}) - (\bar{s_i})^2\ v \times m^2=(m\sum_{i=1}^{m}{s_i^2}) - (\sum_{i=1}^m{s_i})^2 $$
注意到后面一项是定值,扔出去最后计算。现在考虑对于前面一项除去 $m$ 进行 dp 求最小值。记 $sum_i$ 为前缀和,$f_{i,k}$ 为走完第 $i$ 段路,前面分了 $k$ 段的 $s_i^2$ 和的最小值,则状态转移方程为:
$$ f_{i,k} = \min_{j=0}^{i-1}{f_{j,k-1} + (sum_i - sum_j)^2} $$
化简得
$$ f_{i,k} = \min_{j=0}^{i-1}{-2sum_i \times sum_j + f_{j,k-1} + sum_j^2} + sum_i^2 $$
此时我们有 $v_j=-2sum_j, w_i=sum_i, h_j=f_{j,k-1}+sum_j^2$。观察数据可知 $-v_j, w_i$ 均递增,单调队列维护即可。
注意到我们若直接表示一批任务的完成时间,则它与段数有关,不好做,考虑优化表示方式。
我们可以考虑表示做一批任务的准备时间 $s$ 对后面任务的影响:多了准备时间 $s$,那后边的任务都要延迟 $s$ 分钟,代价多了 $(sum_n - sum_{i-1})\times s$。记做完 $i$ 个任务的最小代价(加上准备时间对后面任务的代价)为 $f_i$,这样我们可以列出转移方程: $$ f_i=\min_{j=0}^{i-1}{f_j+sumt\times (sumc_i-sumc_j) + s \times (sumc_n - sumc_j)} $$ 化简得 $$ f_i=\min_{j=0}^{i-1}{-sumc_j\times sumt_i+f_j-s\times sumc_j}+s\times sumc_n+sumt_i \times sumc_i $$ 此时我们有 $v_j=-sumc_j, w_i=sumt_i, h_j=f_j-s\times sumc_j$,观察数据可知 $v_j, w_i$ 均递增,单调队列维护即可。
状态转移方程与上一题相同,观察数据可知,$v_j$ 递增但不严格递增,这说明我们需要特判斜率为 $\infty$ (或 $-\infty$)的情况。$w_i$ 并不具有单调性,单调队列+二分斜率即可。
和前面差不多,不讲了。
P4655 [CEOI 2017] Building Bridges
第 $i$ 根柱子不拆除的最小代价为 $f_i$,则我们有状态转移方程: $$ f_i=\min_{j=0}^{i-1}{f_j+(h_j-h_i)^2+sum_{i-1}-sum_j} $$ 化简得 $$ f_i=\min_{j=0}^{i-1}{-2h_j\times h_i+f_j+h_j^2-sum_j}+sum_{i-1}+h_i^2 $$ 此时我们有 $v_j=-2h_j, w_i=h_i, h_j=f_j+h_j^2+sum_j$。观察数据可知 $v_j, w_i$ 均无单调性,李超线段树维护一次函数即可。
矩阵快速幂优化
CF176B Word Cut
原题太简单了,我们考虑 $n \le 10^6$,$k \le 2^{10^5}$ 怎么做。
手搓小数据可以发现:对于长度为 $n$ 字符串 $s$,它进行操作后的结果 $t$,总有一个整数 $k\in[0,n)$,使得 $s_i=t_{(i+k)\bmod n}$。
首先我们有简单的 dp:记 $f_{i, j}$ 为做了 $i$ 次操作,$k$ 的定义如上,我们有 $f_{i, k}=\sum\limits_{j \ne k 且 j \le n}f_{i - 1, j}$,初始状态为 $f_{0,j}=\begin{cases}1&j=0\0&j\ne0\end{cases}$。
继续观察我们可以发现,因为 dp 转移对称性,在任何时刻,$j\ne0$ 的 $f_{i, j}$ 值都相同。可以这么理解:考虑打乱下标之后 dp,发现值仍不变。
所以我们可以把 $1 \sim n - 1$ 缩起来,转移方程式简化为:$f_{i,0}=(n-1)f_{i-1,1}, f_{i, 1} = f_{i-1,0}+(n-2)f_{i-1,1}$。
显然可以矩阵快速幂优化。我们的初始矩阵为
$$ \begin{bmatrix} 1 & 0\ \end{bmatrix} $$
我们的转移矩阵为
$$ \begin{bmatrix} 0 & 1\ n - 1 & n - 2\ \end{bmatrix} $$
最后统计答案时,把 $start$ 复制一遍接到后面,跑一遍 KMP 找到所有和 $end$ 匹配的开始位置,加入答案即可。
时间复杂度 $O(\log k + n)$。
数据结构优化
CF1557D Ezzat and Grid
记 $f_i$ 为选第 $i$ 行最多保留的行数,显然我们有 $f_i = \max\limits_{j 与 i 在有 1 位置有交}f_j + 1$。这样的时间复杂度是高于 $O(n^2)$ 的,考虑优化。
我们发现,对于“在 $1$ 位置有交”的判断可以改为“在所有 $1$ 位置上转移”,这是显然的。先跑一遍离散化,然后在 $i$ 所有的 $1$ 位置上查询 $f$ 最大值,$+1$ 后把这些位置上的 $f$ 值全部改为 $f_i$。
P12912 [POI 2020/2021 R2] 收拾背包 / Pakowanie plecaka
树形 dp
状态设计
CF780F Axel and Marston in Bitland
太逆天了这题!
$\mathcal{LFN}$