小学生都能看懂的FFT(无修改娱乐)

# 小学生都能看懂的 FFT！！
作者(小学生)其实学这个学了两个月，但我相信你只要努力，就能成功

好的，废话不多说，正片开始

# FFT 章节1:了解 FFT 是干嘛的

[oiwiki](https://oi-wiki.org/math/poly/fft/)：`FFT` 支持在  $O(n\log n)$ 的时间内计算两个 $n$ 次多项式的乘法，比朴素的 $O(n^2)$ 算法更高效。由于两个整数的乘法也可以被当作多项式乘法，因此这个算法也可以用来加速大整数的乘法计算。

我自己的理解就是可以加速多项式的运算，比如多项式乘法，多项式求逆，多项式开根......大部分都可以用 `FFT` 来计算

# FFT 章节2：复数

有些人可能会有点害怕，但是不要怕，这东西虽说是高中到大学的，但是理解起来还是很简单的

首先我们先要弄明白实数

实数是么子东西？实数是由有理数与无理数组成的，有理数又是什么？

有理数是只我们常见的整数，分数，有限小数小数，无限循环小数组成

有人会问：wxy，那无限不循环小数是什么呢?无限不循环小数是无理数，如： $\pi\ e \ Φ...$ 还有 $\sqrt{2}\  \sqrt{3}...$

如果你看不懂 $\ e \ Φ...$ 还有 $\sqrt{2}\  \sqrt{3}...$ 没关系，本文中就只要 $\pi$ 就行

$\pi$ 是什么？是一个圆的 $\frac{周长}{直径}$，约等于 $3.1415926535....$，当一个圆的直径为 $1$ 时，这个圆的周长为 $\pi$

现在明白实数是什么了吧，那么虚数呢？

虚数，是建立在实数之外的一种数，他打破了不能给负数开根号的限制，根号是什么东西，简单来说对于 $a>0$，都有 $\sqrt{a}\times\sqrt{a}=a$,就是这么个意思，我们去想，在实数轴上面，是不是找不到一个数的平方等于 $-1$ ,因为正数乘上正数等于正数，负数乘上负数也等于正数，根本找不到，所以说就有了虚数这么个东西

虚数：$i=\sqrt{-1}$，定义就是这么简单，我们称这个 $i$ 叫做 $虚数i$

小公式（请自行理解）：$\sqrt{-a}=i\sqrt{a}$

实数的运算法则大多数都可运用道虚数上,那么复数又是什么呢

复数可以这么理解，复数有三大类：实数，虚数，实数+虚数

其实这三大类都可以用 $a+bi$ 这个式子来表示，其中 $a,b$ 均为实数，第一大类其实就是当 $b=0$ 时的情况，第二大类其实就是 $a=0$ 时的情况，第三大类其实就是 $a,b$ 均为实数的情况

因此 $a+bi$ 被我们称为虚数的表示方法，当然，还有别的表示方法，下面会讲

c++中有自带的虚数库，叫做 $complex$，用法如下

```c++
#include<complex>//complex头文件
using namespace std;
...
complex<int>x;//定义一个实数部分和虚数部分均为整数的虚数，其实就是a+bi中的a和b都为int类型
x.real();//a+bi中的a
x.imag();//a+bi中的b
```

当然，我们也可以自己去定义，由于需要加减乘除的运算，这里我赘述一下

$$
复数的加法:\\
(a+bi)+(c+di)=a+c+bi+di=(a+c)+(b+d)i\\
复数的减法:\\
(a+bi)-(c+di)=a-c+bi-di=(a-c)+(b-d)i\\
复数的乘法:\\
(a+bi)(c+di)=ac+adi+cbi+bdi^2\\
因为i^2=-1\\
所以ac+adi+cbi+bdi^2=(ac-bd)+(ad+cb)i\\
复数的除法\\
\frac{a+bi}{c+di}=....=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i
$$

**注意:在复数中是没有大小关系的**

# FFT 章节3：多项式

了解多项式，我们先要了解单项式，单项式是未知数，数字的乘积，如：$5x,\pi x^2,3x$ 这种就是单项式

单项式的一般形式可以写为：$ax^k$，其中 $a$ 为系数，$k$ 为次数

多项式就是有多个单项式相加减的来，两个次数相同并且未知数相同的单项式我们将他们称之为同类项

一个 $n$ 次多项式就是有 $n$ 个多项式相加减，其中，这些单项式的次数分别为 $0,1,2,3,4,5$，例如一个 $5$ 次多项式有：$3+5x+4x^2+2x^3+x^4+x^5$,$3$ 是常数项

一个n次多项式的一般形式为：$\sum_{i=0}^{n}a_ix^i$

其中 $a_i$ 是 $i$ 次项的系数，$i$ 为 $i$ 次项的系数

当然，我们通常使用函数来表示多项式，比如说多项式  $A(x)=\sum_{i=0}^{n}a_ix^i$，我们称这个函数为多项式 $A$

那么为什么要用函数来表示呢，比如说我要求出多项式  $A(x)=x^2+2x-3$ 在 $x=2$ 时的值，我们就相当于求  $A(2)$ 的值，只要把 $A$ 的式子展开，然后将式子中的 $x$ 给替换成 $2$ 就行了

# FFT 章节4：单位根

刚才我们学习了复数，现在我们来讲单位根是什么

要了解单位根，首先要知道什么是复平面

复平面简单来说就是一个 **平面直角坐标系** ，只不过  $y$ 轴上面的不再是 $1、2、3、4、5...$了，而是 $i、2i、3i、4i、5i....$。

在这个复平面上，我们可以表示出复数，通俗来讲，一条数轴可以表示出实数，两条数轴可以表示出虚数和实数，一个复平面可以表示出复数！！！

图解: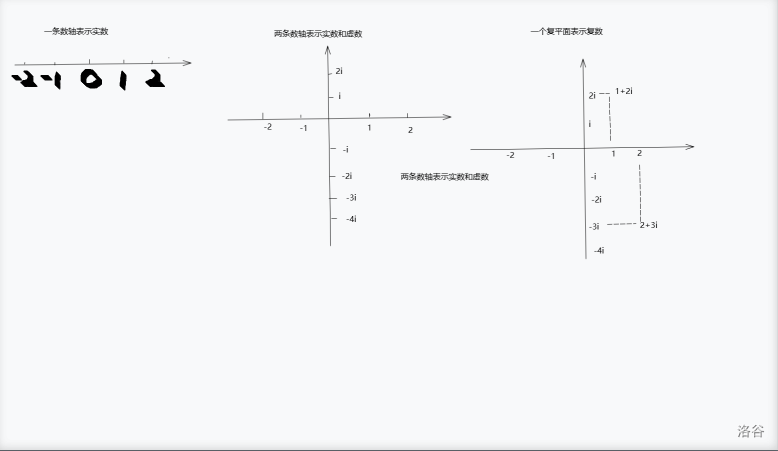
![](https://cdn.luogu.com.cn/upload/image_hosting/057pdbm2.png)

在复平面上以 $(0,0)$ 为圆心，$1$ 为半径，画一个圆，这个圆就被我们称为单位圆

## 单位根章节分块:弧度制

弧度制也就是在单位圆上表示角度的一种方法，比如说，我们要说 $30^\circ$，我会改成 $\frac{\pi}{6}$，这是怎么改过来的呢，其实有一个很好记的方法，因为单位圆的周长是 $2\pi$，所以我们也可以认为 $2\pi就是360^\circ$，则$\pi也就是180^\circ$，为了简便，我就写成  $\pi=180^\circ$

弧度制的意义是什么？我们可以这么理解：$\pi=180^\circ$ 的意思相当于在单位圆上从 $(1,0)$  这个点逆时针旋转 $\pi$，所得的点和原来点组成的角的夹角就是 $180^\circ$

接下来我就可以开始讲第二中复数的表示方法了

著名的欧拉公式就是 $e^{ix}=\cos x+i\sin x$，这个式子在复平面上是很好理解的，其中 $x$ 是弧度制数，在单位圆上旋转 $x$，得到的点的横坐标正好就是 $\cos x$，纵坐标也正好是 $\sin x$，由于这个是复平面，所以纵坐标 $\sin x$ 要乘上一个 $i$，所以得出结论 $e^{ix}$ 的意义就是从 $(1,0)$ 这个点沿着单位根旋转 $x$，得到的那一个点（其实就是数）

至于单位根的详细证明，可以看[yhc写的高级论文(我都看不懂)](https://www.luogu.com.cn/article/px8o0vis)

欧拉公式就是这么来的 $e^{i\pi}=\cos \pi+i\sin \pi=-1$，也就是从 $(1,0)$ 这个点沿着单位根旋转 $\pi$，得到的那一个点，正好落在 $(-1,0)$ 上

于是，一个复数就可以被表示为 $re^{ix}$，$e^{ix}$ 用来确定角度，$r$ 来确定从 $(0,0)$ 伸出去的长度

那么现在可以开始讲单位根是什么了吧

单位根就相当于把单位圆给分成了 $n$ 等分，取其中的 $1$ 份

算了说出来吧，$w_n$ 表示将单位单位圆给分成了 $n$ 等分，其中的 $1$ 份，他的公式为

##  $w_n=e^{i\frac{2\pi}{n}}$

，那么取其中的两份并不是 $2w_n$，而是 $w_n^2$，也就是说n等分分别是 $w_n^0、w_n^1、w_n^2、w_n^3、w_n^4、w_n^5......$，如下图，讲单位圆分成八等份，那个右上角的那个红点就是 $w_8$，最上面那个点就是 $w_8^2$，以此类推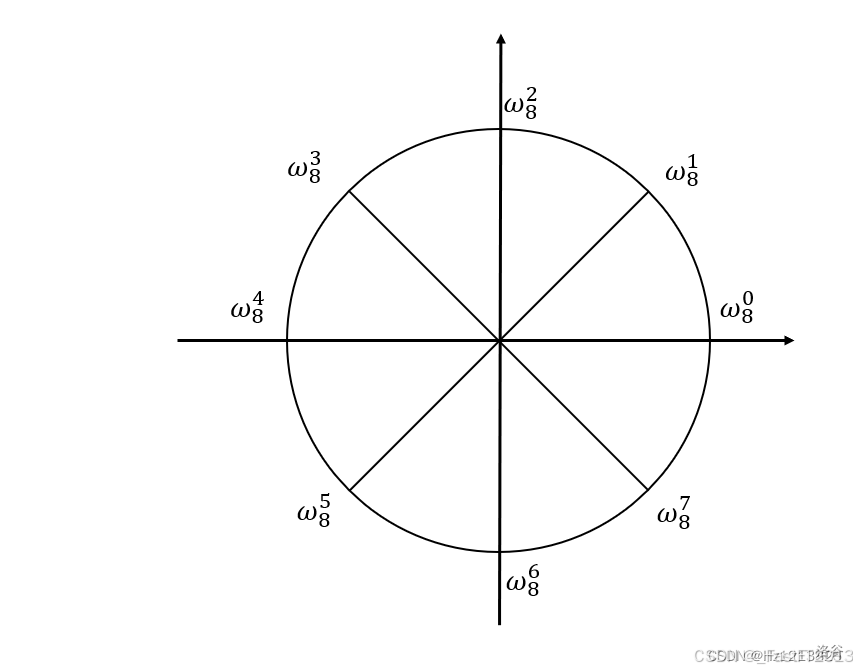

![在这里插入图片描述](https://cdn.luogu.com.cn/upload/image_hosting/wagcw7q3.png)

公式:

## $w_{rn}^{rk}=e^{i\frac{2\pi kr}{nr}}=e^{i\frac{2\pi k}{n}}=w_n^k$

## $w_n^{n}=w_n^0=1$（很显然，看图都可以看出来）

## $w_n^{k+\frac{n}{2}}=-w_n^k$（这个看图也可以看出来）

# 你以为现在已经很难了吗，不！后面更难

# （正片开始）FFT 章节5：FFT 正变换的原理及代码实现

首先我们要先学习一下 `DFT` 的原理

我们要将 $A$ 和 $B$ 相乘，普通的步骤为，直接相乘，次数相加对吧，写一个伪代码

```c++
定义两个整数n，m，表示多项式A和B的项数（不是次数）
定义三个数组A，B，C，分别表示多项式A的系数，多项式B的系数，多项式A和多项式B的乘积的系数
for 0~n-1 cin>>A[i]
for 0~m-1 cin>>B[i]
for i to 1~n-1
    for j to 1~m-1
        	C[i+j]+=A[i]*B[j]//两个单项式相乘为他们的次数相加，系数相乘
    
```

这样的时间复杂度是 $O(n^2)$ 的

我们知道，可以用 $n$ 个点来表示一个 $n-1$ 次多项式，这个我在[浅析.拉格朗日插值](https://blog.csdn.net/gxzssyh/article/details/141127618)里面提到过

FFT的步骤是这样的:
$$
多项式A和B->\\
将多项式转化为多个点->\\
将每个点的因变量给乘起来，得到多项式A\times B的多个点->\\
通过高斯消元得到多项式A\times B
$$
如果单纯使用高斯消元和多点求值，时间复杂度还是 $O(n^3)$，虽说有 $O(n\log^2 n)$ 的多点求值，但是高斯消元依然是 $O(n^3)$，我就不建议大家用这种方法

`FFT` 是怎么将多项式转化为多个点的呢？

比如说 `DFT` 要将多项式 $A(x)=x^2+2x-3$，我们要将他转换为 $4$ 个点，也就是我们自己要选择四个数，然后把这四个数分别带入到 $A(x)$ 中，求出来值，暴力的想法是随机四个值，然后求出这些值在 $A(x)$ 中的值，时间复杂度 $O(n^2)$，我们不妨换一种想法，取两个多项式分别是  $A_0(x)$ 和 $A_1(x)$，$A_0(x)$ 中存储的是 $A(x)$ 的偶数次项，$A_1(x)$ 中存储的是 $A(x)$ 的奇数次项

$$
A(x)=x^2+2x-3\\
A_0(x^2)=x^2-3\\
A_1(x^2)=2\\
A_0(x)=x-3\\
A_1(x)=2\\
A(x)=A_0(x^2)+xA_1(x^2)
$$

为什么要这么做呢？因为这样一来，$A_0(x^2)$ 就是一个偶函数，$A_1(x)$ 就是一个奇函数，我们选的点值只要是一正一负的就行了

意思就是:

$$
A(x)=A_0(x^2)+xA_1(x^2)\\
A(-x)=A_0(x^2)-xA_1(x^2)
$$

则这的规模只有原来的一半，并且求解 $A_0(x)$ 和 $A_1(x)$ 也可以使用这个方法，不过在进行之前，我们要将项数 $n,m$ 给变成一个比他们两个的和都要大并且还是 $2$ 的正整数次幂的数，放心，因为它既时项数变大了，但是他的那些高次项的系数依然是 $0$，毫无差别，只不过你的数组要开打 $3$ 倍

```c++
定义两个整数n,m，表示多项式A和B的项数（不是次数）
int l;//为多项式的2的正整数次幂的项数
while(l<=n+m)l<<=1;
```

你以为这就行了嘛？不，这种方法有漏洞，你们尽然没看出来？

我们取一正一负，但是 $A_0，A_1$ 取得是 $x^2$，在实数范围内，$x^2$ 一直是非负整数，所以就取不了，那么什么数可以在平方后还能保证一正一负呢，答案是单位根，我们使用单位根代替 $x$  来看看

$$
A(w_n^k)=A_0(w_n^{2k})+w_n^kA_1(x_n^{2k})\\
=A_0(w_\frac{n}{2}^{k})+w_n^kA_1(x_\frac{n}{2}^{k})\\
A(w_n^{k+\frac{n}{2}})=A_0(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A_1(x_n^{2k+n})\\
=A_0(w_\frac{n}{2}^{k})-w_n^kA_1(x_\frac{n}{2}^{k})
$$

并且 $A_0,A_1$ 的长度正好是 $\frac{n}{2}$，所以说我们可以将 $A_0,A_1$ 也这样处理就没问题了

注意边界：当项数为 $1$ 时，直接 `return`，因为只剩下常数项了，无论多项式里是什么数答案都是那个常数项

时间复杂度：$O(n\log n)$

```c++
#define PI acos(1.0)
//使用反三角函数求PI
void FFT(complex<double>a[],int n){//多项式和他的项数
	if(n==1)return;
    complex<double>a0[n/2+1],a1[n/2+1];//两个多项式A0和A1
    for(int i=0;i<n;i+=2){//注意，这里必须是<n,因为n是项数
        a0[i/2]=a[i];
        a1[i/2]=a[i+1];
    }//将系数装填进去，理解不了自己在纸上画一画
    FFT(a0,n/2),FFT(a1,n/2);//递归求解
    complex<double>w(cos(2*PI/n),sin(2*PI/n)),W(1,0);//根据单位根的定义创建单位根
    for(int i=0;i<n/2;i++){
        a[i]=a0[i]+W*a1[i];
        a[i+n/2]=a0[i]-W*a1[i];
        W*=w;//W为w_n^i
	}
}
```

# FFT 章节6：FFT 逆变换，IFFT 的原理及实现

我们已经得到了 $A\times B$ 的点值表示，我们现在要通过他的点来得到他本身

简化一下，意思就是你已经知道了多项式 $C$ 的点值表示，我们要求出他的系数表示

一个简单的想法，我们知道 $C$ 的系数，我们只要把他的点值表示带入高斯消元就可以了，具体怎么干去看我的[浅析.拉格朗日插值](https://blog.csdn.net/gxzssyh/article/details/141127618)，但是这样的时间复杂度为 $O(n^3)$，是在是不好用

那么傅里叶是怎么干的呢？(注意:以下用了许多 $\LaTeX$，请读者务必反复阅读，如果真读不懂那就直接看结论算了)
$$
我们将多项式 C 的点值表示也看作一个 n-1 次多项式，记作 D\\
将 D 也进行一次 FFT，得到多项式 F，只不过这次的 FFT的单位根不再是w_n^k了，是w_n^{-k}\\
则：\\
F_k=\sum_{i=0}^{n-1}D_i(w_n^{-k})^i\\
=\sum_{i=0}^{n-1}(w_n^{-k})^i\sum_{j=0}^{n-1}C_j(w_n^i)^j\\
=\sum_{j=0}^{n-1}C_j\sum_{i=0}^{n-1}(w_n^{-k})^i(w_n^i)^j\\
=\sum_{j=0}^{n-1}C_j\sum_{i=0}^{n-1}(w_n^i)^{-k}(w_n^i)^j\\
=\sum_{j=0}^{n-1}C_j\sum_{i=0}^{n-1}(w_n^i)^{j-k}\\
那么这个东西我们怎么对其进行简化呢？\\
我们设函数G(n,j,k)=\sum_{i=0}^{n-1}(w_n^i)^{j-k}\\
那么当j=k时，G(n,j,k)明显等于n\\
当j≠k时,G(n,j,k)经过等比数列求和公式得：\\
G(n,j,k)=\frac{(w_n^{j-k})^n-1}{w_n^{j-k}-1}\\
=\frac{(w_n^n)^{j-k}-1}{w_n^{j-k}-1}\\
=\frac{1-1}{w_n^{j-k}-1}\\
=0\\
由此可得：G(n,j,k)=n [j=k]意思为当j=k时这个函数等于n，在其他情况下等于0\\
所以：\\
F_k=\sum_{j=0}^{n-1}C_j n [j=k]\\
F_k=nC_k\\
我们就可以得到，C_k=\frac{F_k}{n}
$$
所以，我们只需要得到 $F$ 我们就只需要将它所有的系数全都除以一个 $n$ 我们就得到了 $C$

$F$ 怎么求就不用我多说了吧，在原本的 `FFT` 代码上改就行了

```c++
#define PI acos(1.0)
//使用反三角函数求PI
void FFT(complex<double>a[],int n,int inv){//多项式和他的项数
	if(n==1)return;
    complex<double>a0[n/2+1],a1[n/2+1];//两个多项式A0和A1
    for(int i=0;i<n;i+=2){//注意，这里必须是<n,因为n是项数
        a0[i/2]=a[i];
        a1[i/2]=a[i+1];
    }//将系数装填进去，理解不了自己在纸上画一画
    FFT(a0,n/2),FFT(a1,n/2);//递归求解
    complex<double>w(cos(inv*2*PI/n),sin(inv*2*PI/n)),W(1,0);//根据单位根的定义创建单位根，当inv=1时为正变换，当inv=-1时为逆变换
    //complex<double>w(cos(2*PI/n),inv*sin(2*PI/n)),W(1,0);可以这么写，因为cos(-a)=cos(a),sin(-a)=-sin(a)
    for(int i=0;i<n/2;i++){
        a[i]=a0[i]+W*a1[i];
        a[i+n/2]=a0[i]-W*a1[i];
        W*=w;//W为w_n^i
	}
}
```

好了，现在就是FFT的代码了，时间复杂度为 $O(n\log n)$，空间复杂度为 $O(n\log n)$

什么，你问我怎么用，那你肯定是没听前面的，赶紧去听！！！

对了最后输出时要四舍五入才是正确的哦

# FFT章节7:（FFT优化）非递归版FFT

刚才我们讲了递归版的 `FFT`，这种 `FFT` 可能会然我们递归的次数变多，从而爆栈

并且上面的递归般的做法的空间复杂度也是 $O(n\log n)$ 的，也不好用

于是我们便可以使用非递归版 `FFT`

我们先来解决爆栈的问题

归并排序原本是一种分治递归版的做法，但是他可以进行改进

归并排序的非递归版就是一层一层的往上合并，那么我们FFT可以这么做吗？

答案是：可以，只不过难一点

我们 `FFT` 要分治先要将这个多项式按奇偶项分开，然后合并

我们可以找一下规律

长度：$8$

0 1 2 3 4 5 6 7

0 2 4 6|1 3 5 7

0 4|2 6|1 5|3 7

0|4|2|6|1|5|3|7

什么？你没看出有什么规律？没关系，我来告诉你规律吧

首先，`FFT` 先将长度给定成了二的整数次幂

所以我们观察，$8$ 的二进制下有 $3$ 个 $0$，而这些序列中的数的二进制不超过 $3$ 位

他们改完过后的位置都在自己二进制反转后的位置上

什么？尼稳我为顺么？沃野布吉岛

画个图更理解:

（000）（001）（010）（011）（100）（101）（110）（111）

0 	1	 2	 3	 4 	5 	6 	7

0 2 4 6|1 3	5 7

0 4|2 6|1 5|3 7

0|4|2|6|1|5|3|7

(000)(100)(010)(110)(001)(101)(011)(111)

上面的二进制和下面的二进制是反的

于是我们便可以先将他们变成这样，然后再合并

那么怎么变成这样呢?

朴素 $O(\log n)$：

```c++
int zhuan(int l,int x){//l是0的位数
    int sum=0;
    for(int i=0;i<=l;i++){
        if(x>>i&1){
            sum|=(1<<(l-i));
		}
	}
    return sum;
}
```

那么总共有 $O(n)$ 个数，时间复杂度是 $O(n\log n)$ 的

那么怎么优化呢？我们可以用到递推

递推预处理 $O(n)$，使用 $O(1)$

```c++
rev[0]=0;
for(int i=1;i<l;i++){//注意，这里的l是序列长度
	//rev[i]代表这是i二进制转换后的数值
    rev[i]=rev[i>>1]>>1;
    //先将前面l-1位转换了
    if(i&1){//再将后面那位转换
        rev[i]|=(l>>1);
	}
    //写简便一点
    //rev[i]=(rev[i>>1]>>1)|((i&1)*(l>>1));
}
```

这样我们就将 `rev` 处理完了

这种优化我们成为 **蝴蝶优化**

我们现在处理一下第二个优化

空间优化

我们发现，由于 `FFT` 每次修改 $a_i$ 使都要使用到之前的 $a_i$，于是我们将之前的 $a_i$ 不用数组保存，只需要用两个变量来保存就可以了

最后，我们将 `FFT` 依次合并上去就好了

我们处理完之后的 `FFT` 就变成了这样:

```cpp
void FFT(cp* a,int* rev,int n,int inv){
	for(int i=0;i<n;i++){
		if(rev[i]<i)swap(a[i],a[rev[i]]);//如果没被反转过就反转
	}
	for(int g=1;g<n;g<<=1){//g是递归的长度/2
		cp Omiga=cp(cos(PI/g),inv*sin(PI/g));//
		for(int i=0;i<n;i+=(g<<1)){
			cp omiga=cp(1,0);
			for(int j=0;j<g;j++,omiga*=Omiga){
				cp oo=omiga*a[i+j+g];
				cp aa=a[i+j];
				a[i+j]=aa+oo;
				a[i+j+g]=aa-oo;
			}
		}
	}
}
```

# 注意:接下来主要讲优化

# FFT章节8：(FFT优化)三次变两次

我们 `FFT` 不是需要先将 $A,B$ 两个多项式先都进行一次 $FFT$，然后在对 $A\times B$ 进行一次 $IFFT$

我们怎么进行优化呢？

我们可以将多项式 $A$ 的虚数部分给换成多项式 $B$，然后只对他们进行一次 `FFT`，然后求出他们的平方，随后在返回来就好了

那么此时答案在哪里呢？

$$
其实复数的运算对多项式也有效\\
(A+Bi)^2\\
=(A^2-B^2)+i(2AB)
$$

所以，答案的两倍就是这个进行 `FFT` 后的多项式的虚数部分

# T1:[模版题](https://www.luogu.com.cn/problem/P3803)
# T2:[高精度乘法](https://www.luogu.com.cn/problem/P1919)

# CODE：

```c++
#include<iostream>
#include<complex>
#include<cmath>
#define PI 3.1415926535
#define cp complex<double>
using namespace std;
const int N=1e7+5; 
void FFT(cp* a,cp* w,int n){
	int ll=0;
	while((1<<ll)<n)ll++;
	for(int i=0;i<n;i++){
		int cnt=0;
		for(int j=0;j<ll;j++){
			if((i>>j)&1)cnt+=1<<(ll-j-1);
		}
		if(i<cnt)swap(a[i],a[cnt]);
	}
	for(int g=1;g<n;g<<=1){
		for(int i=0;i<n;i+=(g<<1)){
			for(int j=0;j<g;j++){
				cp oo=w[n/(g<<1)*j]*a[i+j+g];
				cp aa=a[i+j];
				a[i+j]=aa+oo;
				a[i+j+g]=aa-oo;
			}
		}
	}
}
int n,m,l=1;
cp a[N*2],b[N*2];
cp omiga[N*2],comiga[N*2];
int c[N*2];
int main(){
	string x,y;
	cin>>x>>y;
	int n=x.size(),m=y.size();
	for(int i=0;i<n;i++)a[i]=x[n-i-1]-'0';
	for(int i=0;i<m;i++)b[i]=y[m-i-1]-'0';
	while(l<n+m)l<<=1;
	for(int i=0;i<l;i++){
		omiga[i]=cp(cos(2*PI*i/l),sin(2*PI*i/l));
		comiga[i]=cp(omiga[i].real(),-omiga[i].imag());
	}
	FFT(a,omiga,l);
	FFT(b,omiga,l);
	for(int i=0;i<l;i++){
		a[i]*=b[i];
	}
	FFT(a,comiga,l);
	for(int i=0;i<n+m-1;i++){
		c[i]+=int(a[i].real()/l+0.5);
		c[i+1]+=c[i]/10;
		c[i]%=10;
	}
	int lenc=n+m;
	while(!c[lenc])lenc--;
	for(int i=lenc;i>=0;i--){
		cout<<c[i];
	}
    return 0;
}
```

正在渲染内容...