回文树：从模板到黑题

## 前言

本文又名：《回文树：从入门到入土》。

## 回文树

咕

## 回文子串

咕

## 回文划分

### 周期

对于字符串 $S$，若其是某个字符串不断反复组成的，假设该字符串长度为 $p$，则称 $p$ 是 $S$ 的一个周期。

形式化的表达为 $\forall i\in[1,|S|-p],s_i=s_{i+p}$。这里我们定义总是有 $p<|S|$。

> 弱周期引理：若 $p,q$ 都是 $S$ 的周期，并且 $p+q\leqslant |S|$，则 $\gcd(p,q)$ 也是 $S$ 的周期。

不妨假设 $q\geqslant  p$，显然由条件二有 $i-p>0$ 并且 $i+q\leqslant |S|$。那么也一定存在 $S_i=S_{i-p}=S_{i-p+q}$，$S_i=S_{i+q}=S_{i+q-p}$，这说明 $q-p$ 也是 $S$ 的周期。

然后通过辗转相除法得到 $\gcd(p,q)$ 也是 $S$ 的周期。

我们定义字符串 $S$ 中，若长度为 $p$ 的前缀和长度为 $p$ 的后缀相等，则认为这个长度为 $p$ 的前缀 $t$ 是 $S$ 的一个 Border。Border 可以视为将某个前缀右移 $|S|-x$ 的长度。

> 引理 $2$：长度为 $x$ 的 Border 意味着长度为 $|S|-x$ 的周期。因为 $S_i=S_{i+|S|-x}$。

### 匹配

> 引理 $3$：考虑 $|s_1|\leqslant |s_2|\leqslant 2\times |s_1|$，则 $s_1$ 在 $s_2$ 中的所有匹配位置构成等差数列。

![](https://cdn.luogu.com.cn/upload/image_hosting/nbuo6mft.png)

我们考虑匹配次数大于等于 $3$，首先显而易见，任意两次匹配必然存在重叠部分或者相接，我们假设重叠部分为 $|s_1|-d$，我们再假设第二次匹配与第 $x$ 次匹配的重叠部分为 $|s_1|-q$。

那么也就存在 $|s_1|-d$ 是 $s_1$ 的一个 Border，那么根据引理 $2$ 就有 $d$ 是 $s_1$ 的一个周期。同理，$q$ 也是 $s_1$ 的一个周期。

而非常显然第一次匹配与第 $x$ 次匹配也有重叠部分或者相接，重叠部分为 $|s_1|-d-q$，这说明 $d+q\leqslant s_1$，进而说明 $\gcd(d,q)$ 也是 $s_1$ 的周期。

若 $d>\gcd(d,q)$，那第二次匹配应该提前到距离第一次匹配 $\gcd(d,q)$ 的地方。

若 $d=\gcd(d,q)$，则 $d|q$。

这说明任意两个匹配之间的间隔都是 $d$ 的倍数。

由于 $s_{1_i}=s_{1_{i+d}}$（$d$ 是 $s_1$ 的周期），那么也就意味着每隔 $d$ 个字符都会存在匹配。

由此我们证明了引理 $3$，并且知道了 $s_1$ 的最小周期是 $d$。

### Border

> 引理 $4$：字符串 $s$ 所有长度大于等于 $\frac{|s|}{2}$ 的 Border 长度组成一个等差数列。

考虑两个 Border 的长度分别为 $|s|-p,|s|-q$，那么 $p,q$ 都是 $|s|$ 的周期（引理 $2$），接着有 $\gcd(p,q)$ 是 $|s|$ 的周期，然后使用类似证明引理 $3$ 的方法可以得到引理 $4$。

（Border 的本质其实就是拿了一个前缀当刚刚的 $s_1$，拿自己当刚刚的 $s_2$。）

> 引理 $5$，考虑 $|s_1|=|s_2|$，对于所有 $k\geqslant \frac{|s_1|}{2}$ 且 $s_1$ 的 $k$ 长前缀等于 $s_2$ 的 $k$ 长后缀，$k$ 构成等差数列。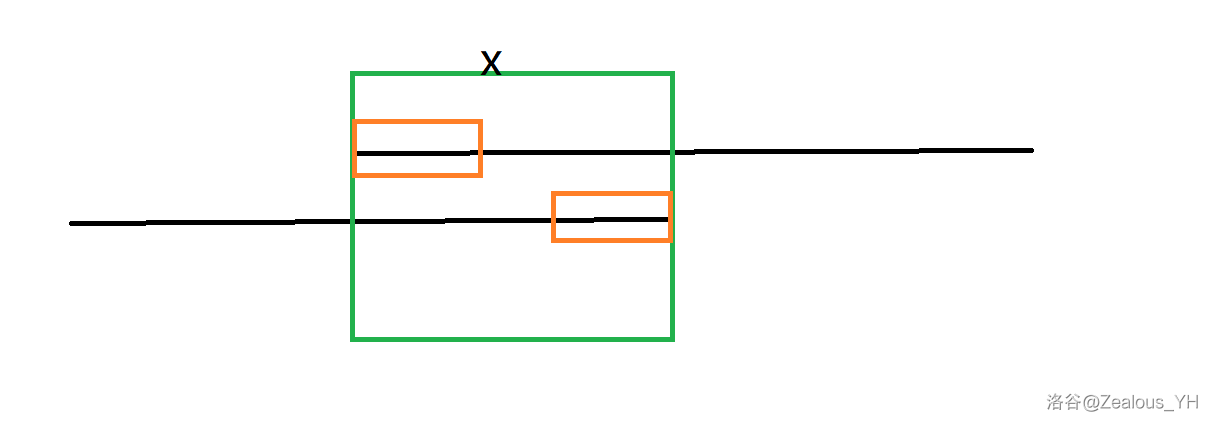

![](https://cdn.luogu.com.cn/upload/image_hosting/ll3chcn1.png)

考虑最大的 $k$ 为 $x$，那么有其它所有的 $k$ 都是 $s_1$ 的 $x$ 长前缀的的 Border。鉴于 $\frac{x}{2}\leqslant \frac{s_1}{2}$，则 $k\geqslant \frac{x}{2}$，根据引理 $4$ 可证。

因此我们可以把一个字符串的 Border 按照 $[1,2),[2,4),[4,8)\cdots$ 分组，这样一组以内的 Border，最小的一定大于等于最大的除以 $2$，满足约束。显然会划分出 $\log |s|$ 个区间，因此得到结论：

字符串 $s$ 的 Border 可以被划分为 $O(\log |s|)$ 个等差数列。

### 回文 Border

显然若 $s$ 是回文串，那么它的后缀 $t$ 是回文串当且仅当是它的 Border。因为 $s$ 中的 Border 必然满足正读相同（不然不是 Border）且反读相同（不然破坏回文）。

那么就有回文串 $s$ 的回文后缀可以被划分为 $O(\log |s|)$ 个等差数列。

我们用到这个结论来解决“回文划分”相关的问题，我们认为这种问题的普遍 dp 形式是：

$f_i=\textrm{func}(f_{j})\land \text{palin}(s[j,i])$，其中 $\text{palin}$ 表示“是回文串”，$\text{func}$ 是某种运算，可能是求和也可能是取 $\min$。此结构并不固定，在 $\text{func}$ 外可能有 $+1$ 等。

下文中我们用“和”来表示 $\text{func}$，其他运算基本同理。我们用 $f$ 表示实际中的 dp 数组。

### slink 指针与 diff

回文树上的节点现在要维护 $diff$，表示相邻两个长度的回文后缀的差，也就是 $len_x-len_{fail_x}$。

$slink_x$ 则是表示 $x$ 所在等差数列的最小一项的节点（同时也是下一个等差数列的最大一项），也就是从 $x$ 沿着 $fail$ 指针向上跳的第一个位置 $y$ 存在 $diff_y\neq diff_x$。

容易发现 $slink$ 的好处是如果我一直向上跳 $slink$ 最多只会跳 $O(\log |s|)$ 下。

维护 $slink,diff$ 非常容易。下面我们看看怎么优化转移。

值得注意的是我们这里仍然采用增量构造，所以 $i$ 是目前加的字符的下标。

我们定义 $g_x$ 表示 $x$ 所在等差数列，从 $x$ 到 $slink_x$ 以前（不含）的 $f$ 值之和，接下来我们考虑从 $g_{fail_x}\to g_x$。

由于每一个回文后缀其实都是等差数列中上一项的回文后缀（$fail_x$ 的字符串是 $x$ 字符串的回文后缀），又因为回文后缀是 Border，所以所有回文后缀向左平移 $diff_x$ 的长度之后就会再次出现（$fail_x$ 第一次出现在 $x$ 右边，第二次会出现在左边）。

因此我现在的这个位置可以看作是 $fail_x$ 的答案向左平移得到的，但是会多出来一些。比如下面这张经典图片（图源 OI-wiki）：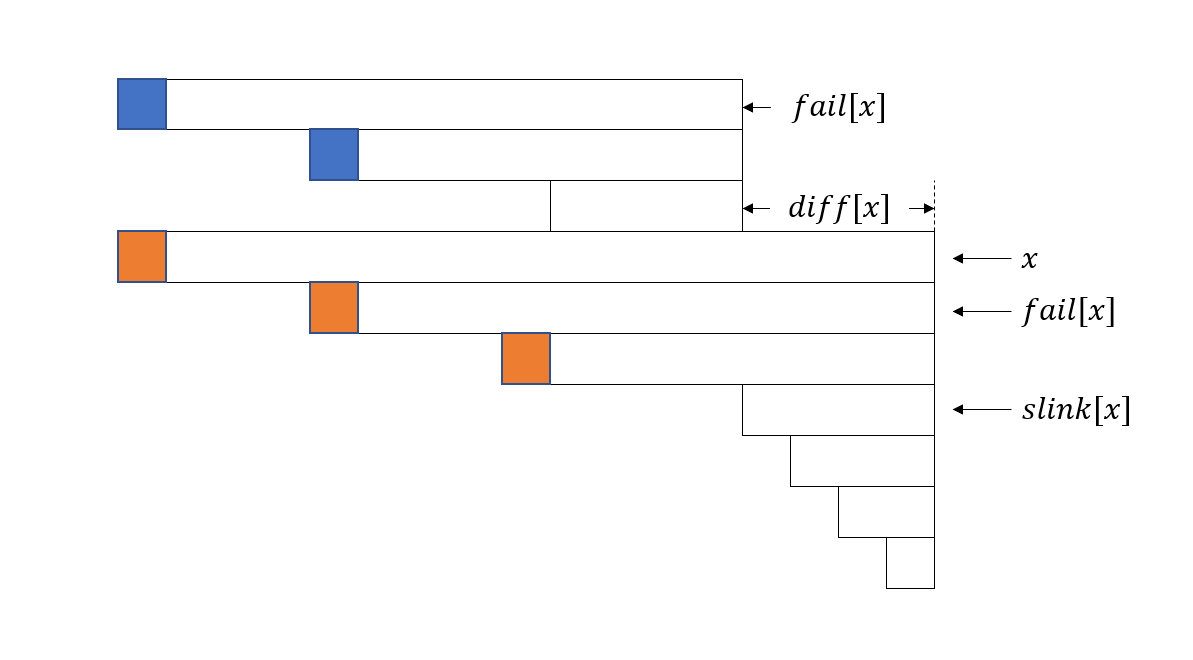

![](https://oi-wiki.org/string/images/pam6.png)

$fail_x$ 向左平移 $diff_x$ 之后，$g_{fail_x}$ 记录的是蓝色的答案，这个值等于橙色的前两个位置的答案，而多出来的那个位置，就是 $slink_{fail_x}$ 左移 $diff_x$ 位变出来的答案。

显然当 $diff_x=diff_{fail_{x}}$ 的时候 $fail_x$ 和 $x$ 的 $slink$ 是一样的。如果不同，那么 $x$ 是这个等差数列的第一项，应该取得自己左移 $diff_x$ 位的答案。综合一下，那个多出来的位置就是 $i-len_{slink_x}-diff_x$，注意这种情况下不能加上 $g_{fail_x}$。

因此我们每次更新完 $g$ 之后更新 $dp$ 就好了，代码如下：

```
insert(c,i);//插入新字符
for(int j=lst;j>1;j=slink[j]){//j>1防止跳到根
	g[j]=dp[i-len[slink[j]]-diff[j]];//多出来的那个值
    if(diff[j]==diff[fail[j]]){//和上一位在同一个等差数列中
   	    g[j]+=g[fail[j]];
    }
    dp[i]+=g[j];//更新dp
}
```

最小回文划分的话，就记录一下 $g$ 是一堆 $f$ 的 $\min$，然后每次找出这个 $\min$ 值再 $+1$ 就可以转移了。

回文划分数基本同理，但是改成记录 $g$ 是一堆 $f$ 的和。

### CF932G Palindrome Partition 题解

下面我们来做黑题。

首先我们构造一个串 $t=s_1s_{n}s_2s_{n-1}\cdots$，容易发现答案就是这个串的偶回文划分数。（$t$ 的偶回文串拆开之后就是两个在两边的相等串）

（P.S. 这是一个经典的 trick，通过交替放法把相等 / 反转后相等的串强行干成回文再解决问题）

偶回文划分数可以用一种相当暴力的方式，我只在偶数处更新 dp 数组，因为符合条件的转移一定来自偶数处（一堆偶回文串拼起来肯定是偶数长度），因此我想从奇数处用奇回文串更新答案时就会得到 $0$，而从偶数处用偶回文串更新答案就可以成功更新。（这也是 OI-wiki 的方法）

当然有一种更加优雅的方法，给 $g$ 加上一维，表示全用奇数转移或者全用偶数转移。用多出来的部分转移时，判断一下 $len_{slink_j}+diff_j$ 的奇偶性，对应加入即可，如果要从 $fail$ 转移，则需要判断一下 $diff$ 的奇偶性，如果 $diff$ 是奇数，就要从奇数转移到偶数，从偶数转移到奇数，反之亦然。（[这篇题解](https://www.luogu.com.cn/blog/ryoku/solution-cf932g)的方法）

```
int len[N],fail[N];
int ch[N][30];
int diff[N];
int slink[N];
ll dp[N];
ll g[N];
int tot=-1;
int lst;
string t;
string s;
int getfail(int i,int x){
    while(t[i-len[x]-1]!=t[i]){
        x=fail[x];
    }
    return x;
}
int newnode(int x){
    tot++;
    len[tot]=x;
    return tot;
}
void insert(int i,char c){
    int now=getfail(i,lst);
    if(!ch[now][c-'a']){
        int cur=newnode(len[now]+2);
        fail[cur]=ch[getfail(i,fail[now])][c-'a'];
        ch[now][c-'a']=cur;
        diff[cur]=len[cur]-len[fail[cur]];
        if(diff[cur]==diff[fail[cur]]){
            slink[cur]=slink[fail[cur]];
        }
        else{
            slink[cur]=fail[cur];
        }
    }
    lst=ch[now][c-'a'];
}
int main(){
    cin>>s;
    s='@'+s;
    t='@';
    int n=s.length()-1;
    fr1(i,1,(n+1)/2){
        t+=s[i];
        if(i==n-i+1){
            break;
        }
        t+=s[n-i+1];
    }
    // cout<<t<<endl;
    n=t.length()-1;
    newnode(0);
    newnode(-1);
    fail[0]=1;
    dp[0]=1;
    fr1(i,1,n){
        insert(i,t[i]);
        for(int j=lst;j>1;j=slink[j]){
            g[j]=dp[i-len[slink[j]]-diff[j]];
            if(diff[j]==diff[fail[j]]){
                g[j]+=g[fail[j]];
                g[j]%=M;
            }
            if(i%2==0){
                dp[i]+=g[j];
                dp[i]%=M;
            }
        }
    }
    cout<<dp[n]<<endl;
    ET;
}
```

正在渲染内容...