斜率优化（一） - 洛谷保存站

先看一道题：[P2365](https://www.luogu.com.cn/problem/P2365 "标题")

显然是DP。

设 $dp_i$ 表示做完前 $i$ 个任务的最短用时，则状态转移方程是：

$dp_i = \min_{0 \le j < i} \{dp_j + (\sum_{k = 1}^i t_k) \times (\sum_{k = j + 1}^i c_k) + S \times (\sum_{k = j + 1}^n c_k)\}$（用了P5785里的数组名）

方程中很多区间和，考虑前缀和优化。对 $t$ 和 $c$ 做前缀和，得到新的转移方程：

$dp_i = \min_{0 \le j < i} \{dp_j + t_i \times (c_i - c_j) + S \times (c_n - c_j)\}$

时间复杂度 $O(n^2)$, 空间复杂度 $O(n)$，足以通过本题。

再看[P5785](https://www.luogu.com.cn/problem/P5785 "标题")，和P2365几乎一模一样，但数据范围是 $1 \le n \le 3 \times 10^5$，$t_i$ 也可能为负，时间复杂度 $O(n^2)$的算法肯定会 $\color{#000060}{TLE}$。 这时，就要请出我们的斜率优化了。

先把 $\min$ 里的式子写成

$(S \times c_n + t_i \times c_i) + (dp_j - S \times c_j) - t_i \times c_j$

的形式，我们发现，$S \times c_n + t_i \times c_i$ 与 $j$ 无关，把他们提出来，得到

$dp_i - S \times c_n - t_i \times c_i = \min_{0 \le j < i} \{(dp_j - S \times c_j) - t_i \times c_j\}$。

现在要做的就是快速算出 $\min_{0 \le j < i} \{(dp_j - S \times c_j) - t_i \times c_j\}$了。

令 $y_j = dp_j - S \times c_j$， $x_j = c_j$，$k_i = t_i$，$b_i = dp_i - S \times c_n - t_i \times c_i$，则 $b_i = \min_{0 \le j < i} \{y_j - k_i \times x_j\}$。这是一个斜率式子，$b_i$ 的几何意义是过点 $(x_j, y_j)$，斜率为 $k_i$ 的直线的最小截距。

要让截距最小，取的那个点一定在下凸壳上。下凸壳上相邻两点间斜率单调，可用单调队列维护。

用二分法选择下凸壳上最优的点，计算 $dp_i$ ，每次计算完 $dp_i$ 后插入新的点 $(x_i, y_i)$。

$1.$ 怎么二分？
>我们知道取得最小截距的点 $j$ 的一个性质：$j$ 一定是满足 $\displaystyle{\frac{y_{j + 1} - y_j}{x_{j + 1} - x_j} > k_i}$ 且最小的点。
>
>所以，我们可以判断 $mid$ 满不满足这个条件，若满足，则到左侧查找，否则到右侧查找。

$2.$ 怎么插入？
>当 $\displaystyle{\frac{y_{tail} - y_{tail2}}{x_{tail} - x_{tail2}}} < \displaystyle{\frac{y_i - y_{tail}}{x_i - x_{tail}}}$（$tail$ 和 $tail2$ 分别代表队尾第一个和第二个数）时，如下图：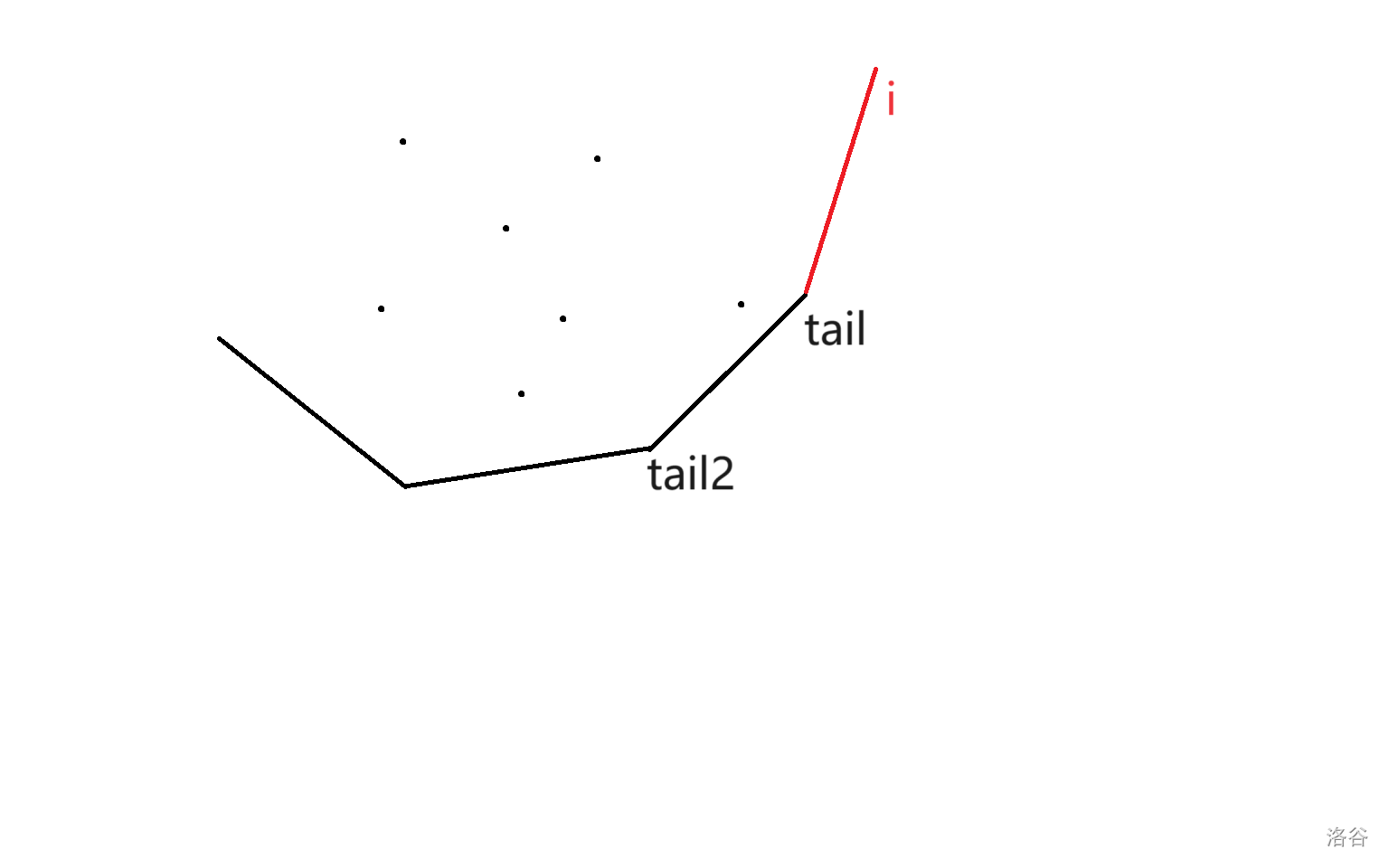
>
>![case_1](https://cdn.luogu.com.cn/upload/image_hosting/0b6pvm0i.png)
>
>直接插入即可。
>
>当 $\displaystyle{\frac{y_{tail} - y_{tail2}}{x_{tail} - x_{tail2}}} \ge \displaystyle{\frac{y_i - y_{tail}}{x_i - x_{tail}}}$ 时，如下图：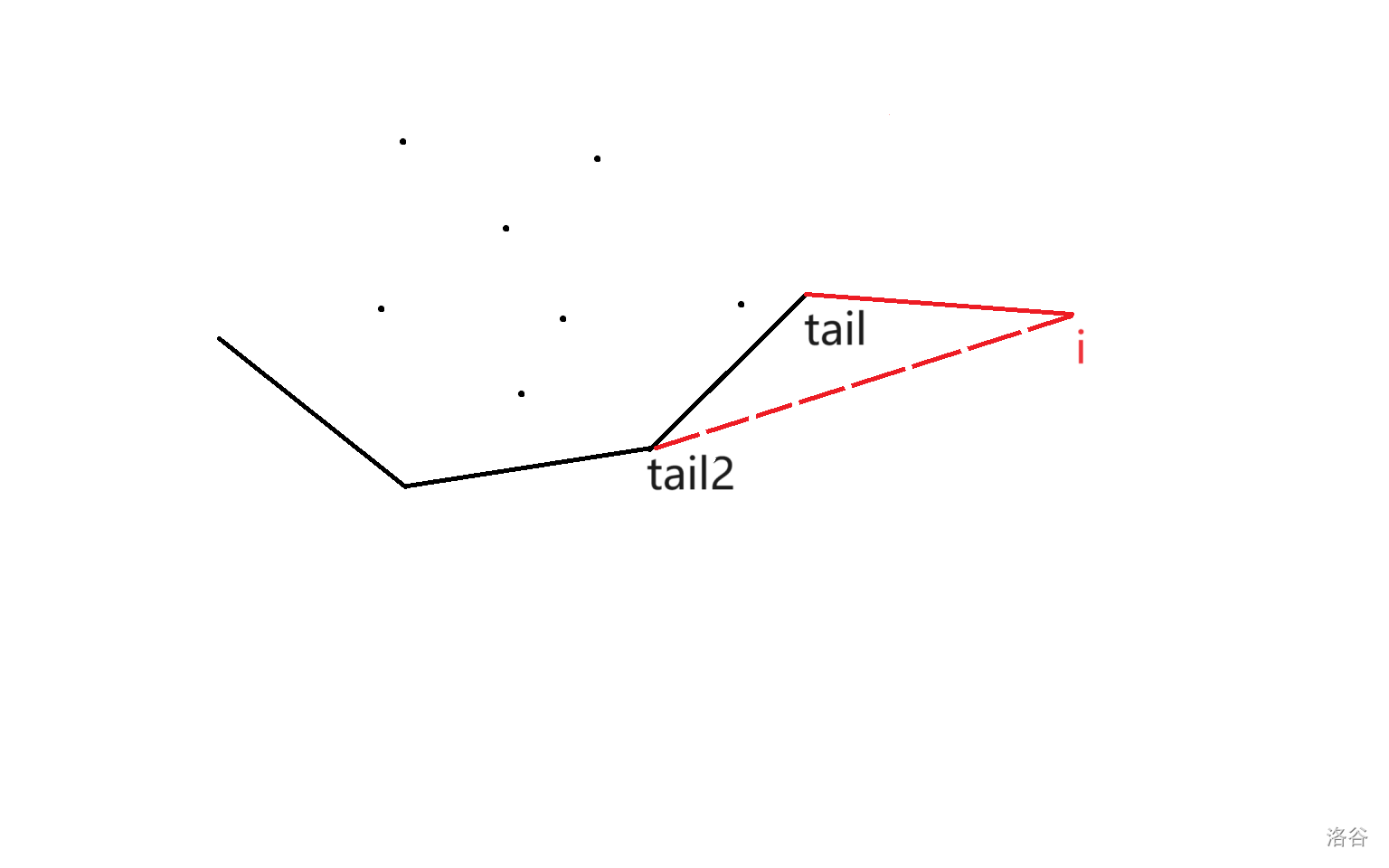
>
>![case_2](https://cdn.luogu.com.cn/upload/image_hosting/gjjgnsoh.png)
>
>这时如果直接插入，就会破坏下凸性，应先删除队尾。重复此操作直到满足 $\displaystyle{\frac{y_{tail} - y_{tail2}}{x_{tail} - x_{tail2}}} < \displaystyle{\frac{y_i - y_{tail}}{x_i - x_{tail}}}$ 或队列中只有一个数，再插入。

每个数至多进出队列各一次，共 $O(n)$，每次二分 $O(\log n)$，总时间复杂度 $O(n \log n)$。

参考代码：

```cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N{300005};
ll t[N], c[N], dp[N], n, s, q[N], tail{};
int main()
{
	cin >> n >> s;
	for(int i = 1; i <= n; ++i)
	{
		cin >> t[i] >> c[i];
		t[i] += t[i - 1];
		c[i] += c[i - 1];
	}
	for(int i = 1; i <= n; ++i)
	{
		int j = tail, l = 0, r = tail;
		while(l <= r)
		{
			int mid = (l + r) >> 1;
			if(dp[q[mid + 1]] - dp[q[mid]] >= (t[i] + s) * (c[q[mid + 1]] - c[q[mid]]))
				r = mid - 1, j = mid;
			else
				l = mid + 1;
		}
		j = q[j];
		dp[i] = dp[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]);
		while(tail && (dp[q[tail]] - dp[q[tail - 1]]) * (c[i] - c[q[tail]]) >= (dp[i] - dp[q[tail]]) * (c[q[tail]] - c[q[tail - 1]]))
			--tail;
		q[++tail] = i;
	}
	cout << dp[n] << endl;
	return 0;
}
```

***注意事项***

计算斜率时，不想被卡精度用乘法，不想溢出用除法。

正在渲染内容...