主页
搜索
最近更新
数据统计
申请密钥
系统公告
1
/
1
请查看完所有公告
欧拉函数
最后更新于 2025-07-31 09:13:26
作者
whx2009
分类
个人记录
复制 Markdown
查看原文
删除文章
更新内容
# 前言: 伟大的教练昨天讲了这个算法,所以来写一写,这段话绝对没有复制粘贴…… # 正文: ## 定义: 一个数的欧拉函数是指这个数字前面(不包含这个数字)有多少数字与他互质,如:2的欧拉函数就是1,3的欧拉函数就是2,4的欧拉函数就是2…… ## 计算: 那么一个数的欧拉函数就是这个数所有质因数被一减掉的乘积在乘上这个数本身。(这里我们可以用到容斥原理去证明,但对于我来说貌似证明没有什么实际作用……算了,我承认我没有听的太懂) 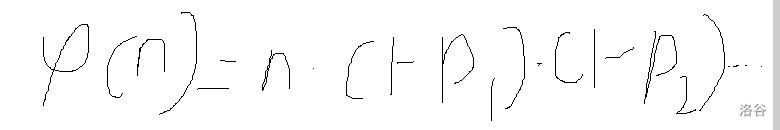 p是n的质因数。 ## 性质: ### 性质一: 如果两个数字$n$,$m$互质,那么φ(n*m)=φ(n)*φ(m); 这个结论还是很好推的,我们只需要上面那个算式即可,两个数互质,那么他们分解出来的质因数自然不一样,我们直接乘起来即可。 ### 性质二: 如果两个数$m$的质因数包含于$n$之中,那么φ(n*m)=φ(n)*m; 这个结论还是很好推的,我们只需要上面那个算式即可,那么他们分解出来的质因数自然有一个全部包含与另一个,我们直接乘m即可。 ### 性质三: 一个数的所有因数的φ加起来是这个数,这个结论懒得推了…… ### 知道了这些,我们就可以用[线性筛](https://www.luogu.com.cn/blog/928579/xian-xing-shai#)强推了。 ```cpp void xs() { for(int i=2;i<=n;i++) { if(pd[i]==0) p[i]=i-1,zs[++cnt]=i; for(int j=1;j<=cnt&&i*zs[j]<=n;j++) { pd[i*zs[j]]=1; if(i%zs[j]==0){p[i*zs[j]]=p[i]*zs[j];break;} p[i*zs[j]]=p[i]*(zs[j]-1); } p[i]=p[i-1]+(p[i]*2); } } ```
正在渲染内容...
点赞
0
收藏
0