Euclidea 题解+证明 - 洛谷保存站

[Euclidea](https://www.euclidea.xyz/) 是一个很好的尺规作图网站，入门教程建议看 Ruthless_killer 的视频

![](bilibili:BV1Gt4y1S7Fm)

## $\text{1.Alpha}$

### $\text{1.* 等边三角形}$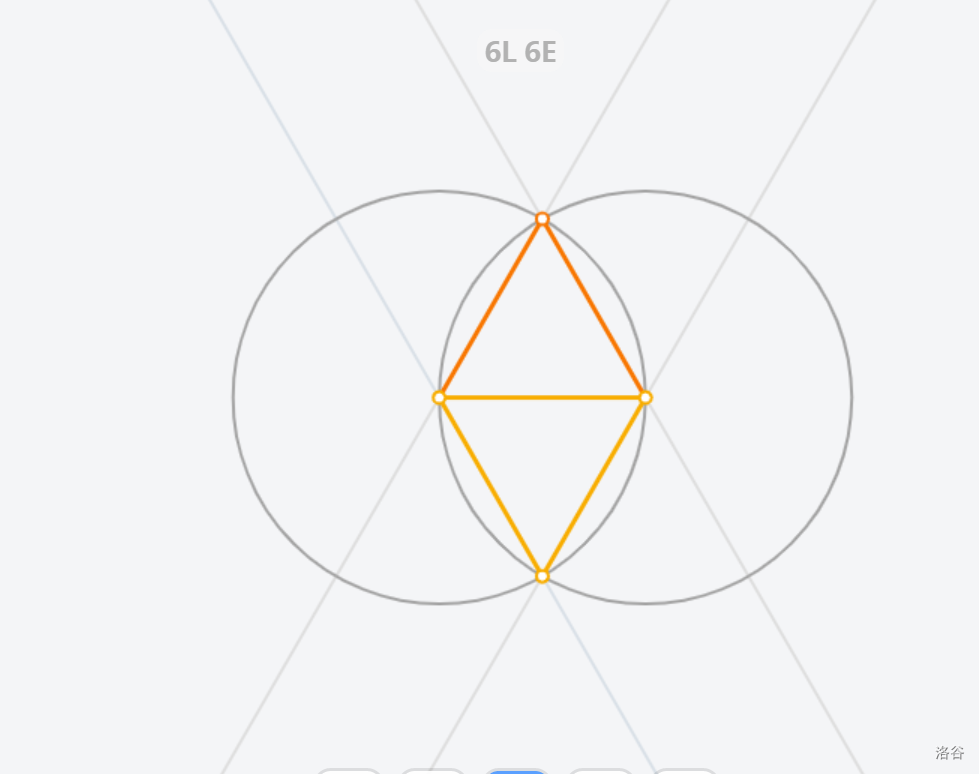

![](https://cdn.luogu.com.cn/upload/image_hosting/ivulyhdr.png)

做法：见视频。

证明：因为半径相等，所以三条边都相等

### $\text{1.1 60}^\circ \text{角}$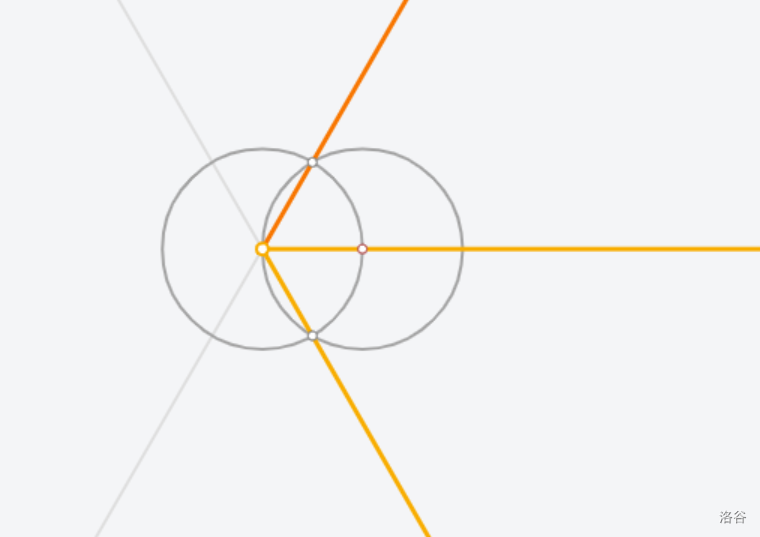

![](https://cdn.luogu.com.cn/upload/image_hosting/56j6oref.png)

做法：以线段两端点为圆心，线段长为半径做两圆，连接线段端点和两圆交点。

证明：等边三角形一角为 $60^\circ$

### $\text{1.* 交点工具}$

略。

### $\text{1.2 中垂线}$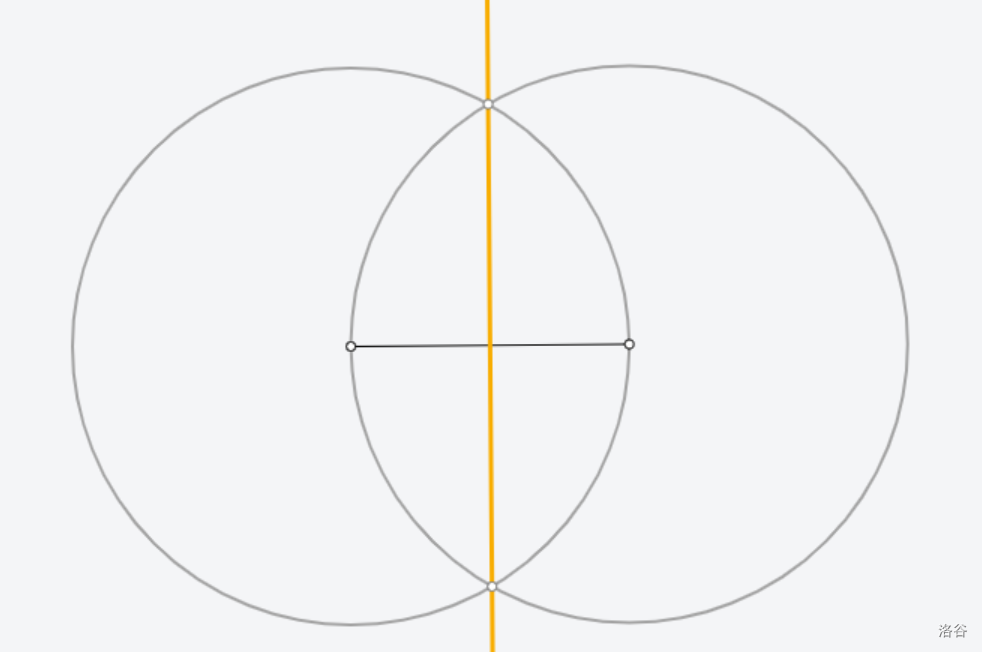

![](https://cdn.luogu.com.cn/upload/image_hosting/kk29nfpl.png)

做法：以线段两端点为圆心，线段长为半径做两圆，连接两圆交点。

证明：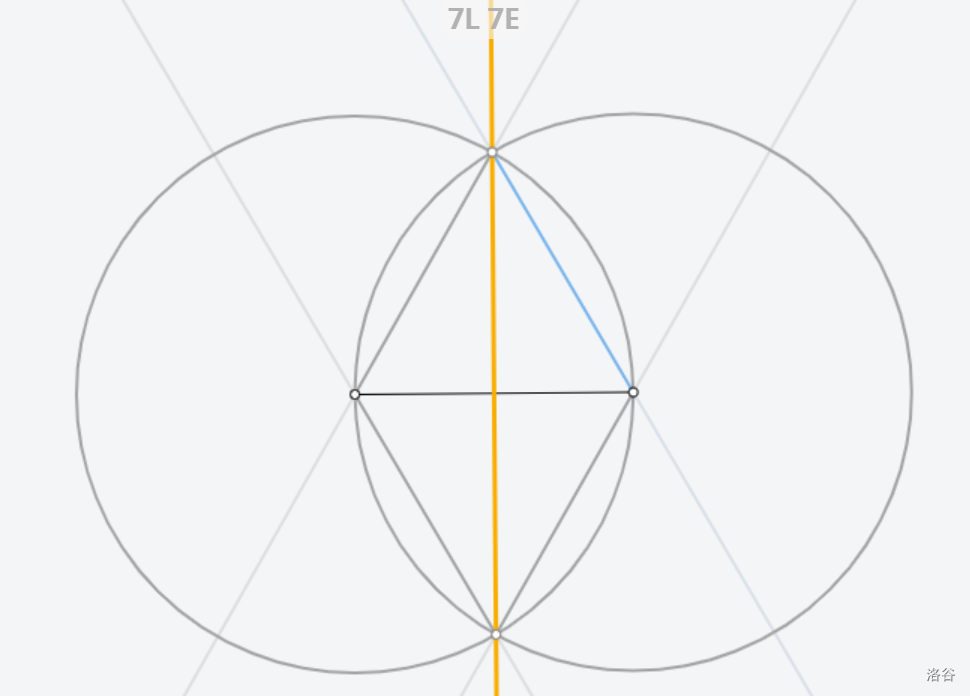

![](https://cdn.luogu.com.cn/upload/image_hosting/0li1ycdb.png)

因为半径相等，所以新连的四边形是菱形，菱形对角线互相垂直平分。

### $\text{1.* 中垂线工具}$

略。

### $\text{1.3 中点}$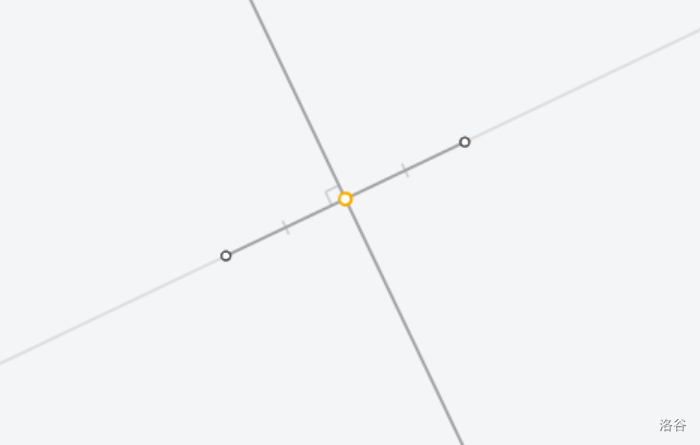

![](https://cdn.luogu.com.cn/upload/image_hosting/536reiot.png)

做法：做两点连线的中垂线。

证明：因为是中垂线，所以中点。

### $\text{1.4 方中圆}$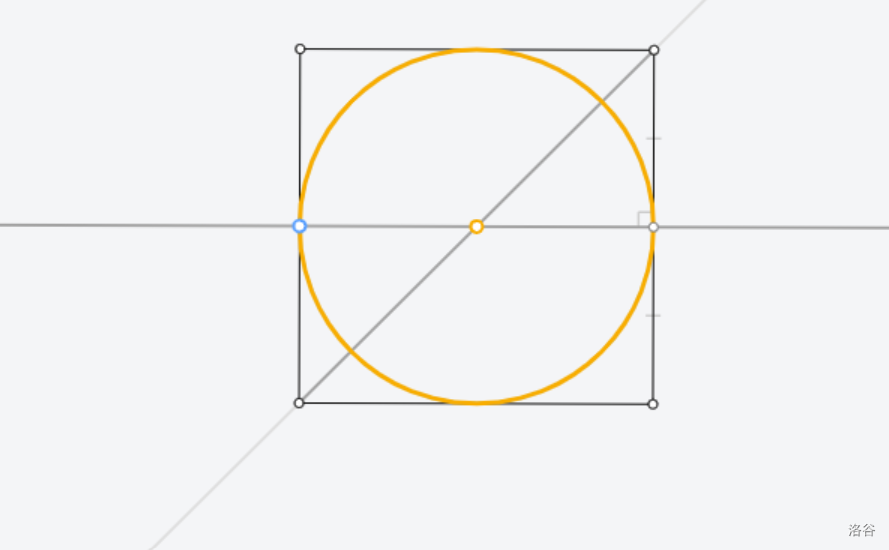

![](https://cdn.luogu.com.cn/upload/image_hosting/laqjl9xd.png)

做法：连一条对角线，做一边中垂线。以两线交点为圆心，一边中点和两线交点的距离为半径，做圆。

证明：做的两条线都是对称轴，所以交点是正方形中心，显然直径是边长。

### $\text{1.* 移动工具}$

略。

### $\text{1.5 正方形内作菱形}$

这题有隐藏star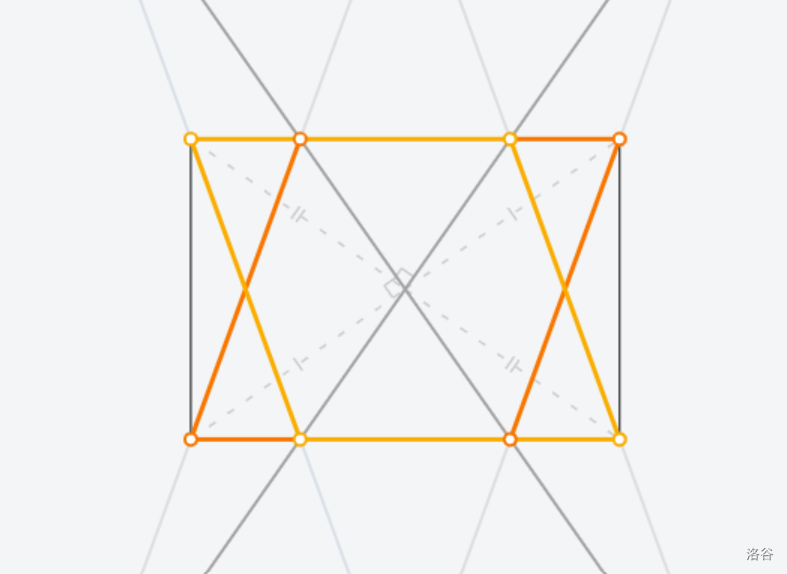

![](https://cdn.luogu.com.cn/upload/image_hosting/hinjt5cs.png)

做法：做对角线中垂线，然后就可以轻松获得四边形四个点位置，用线段连起来。

证明：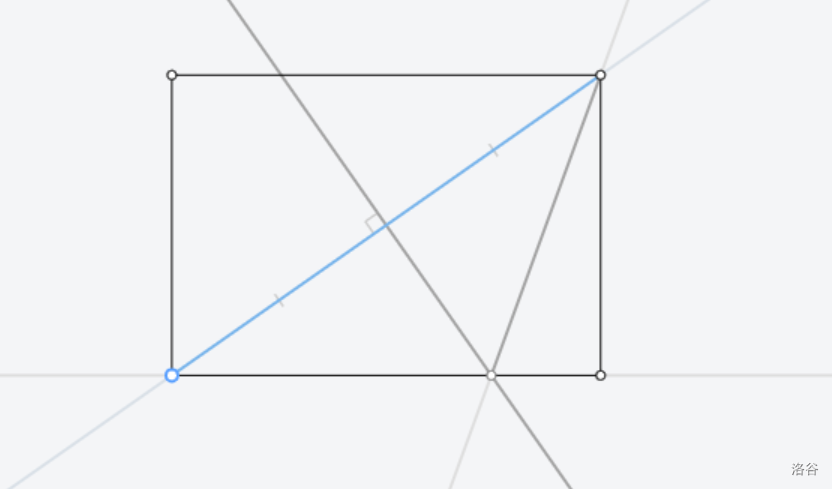

![](https://cdn.luogu.com.cn/upload/image_hosting/h1uterto.png)

显然这是个等腰三角形。所以做出来的四边形四边相等。

### $\text{1.6 圆心}$

没办法一次满足L/E的要求，所以分两次做图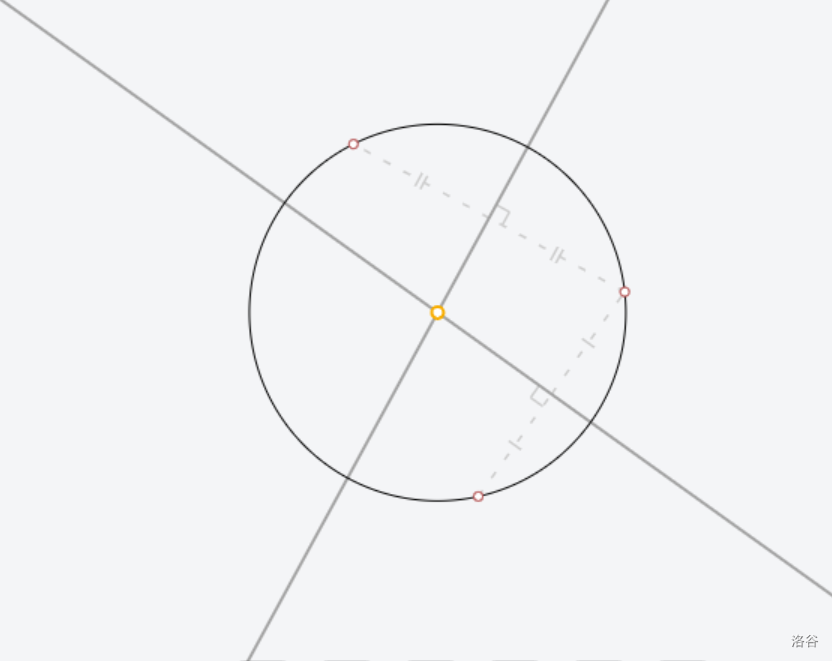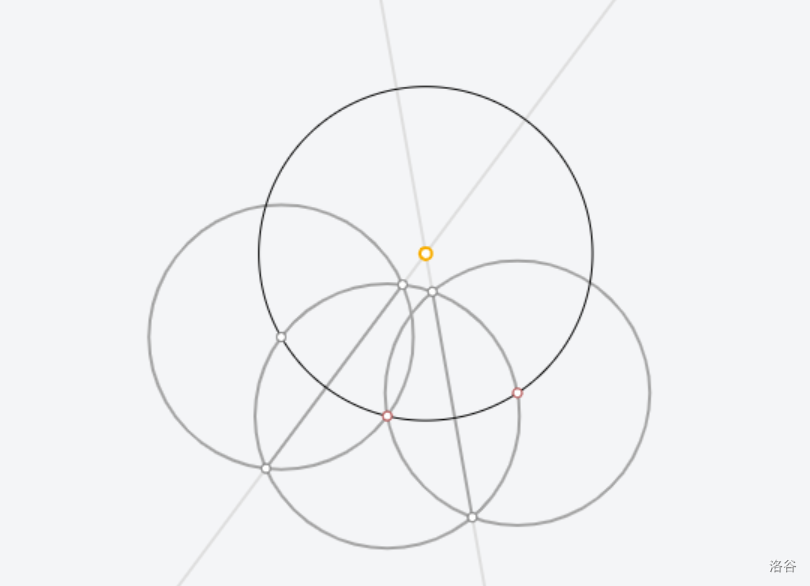

![](https://cdn.luogu.com.cn/upload/image_hosting/ij7qtukv.png)

![](https://cdn.luogu.com.cn/upload/image_hosting/3lh75mvi.png)

1做法：做两条弦的中垂线，交点是圆心。

2做法：中垂线的做法有一个圆被重复用了，画一遍就够了。

证明：弦的中垂线是直径，直径交点是圆心。

### $\text{1.7 圆心}$

没办法一次满足L/E的要求，所以分两次做图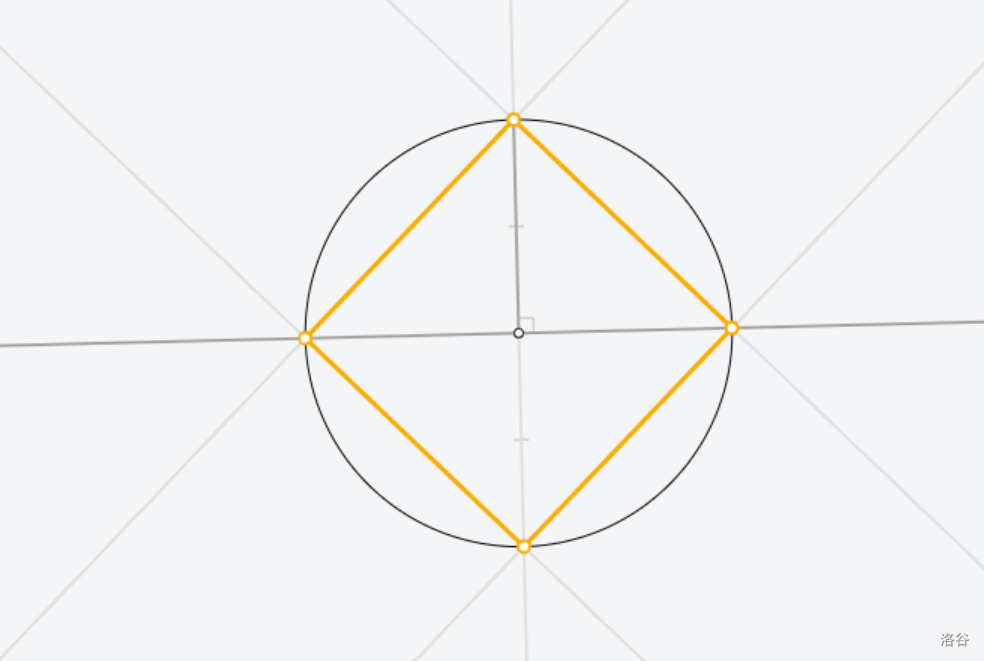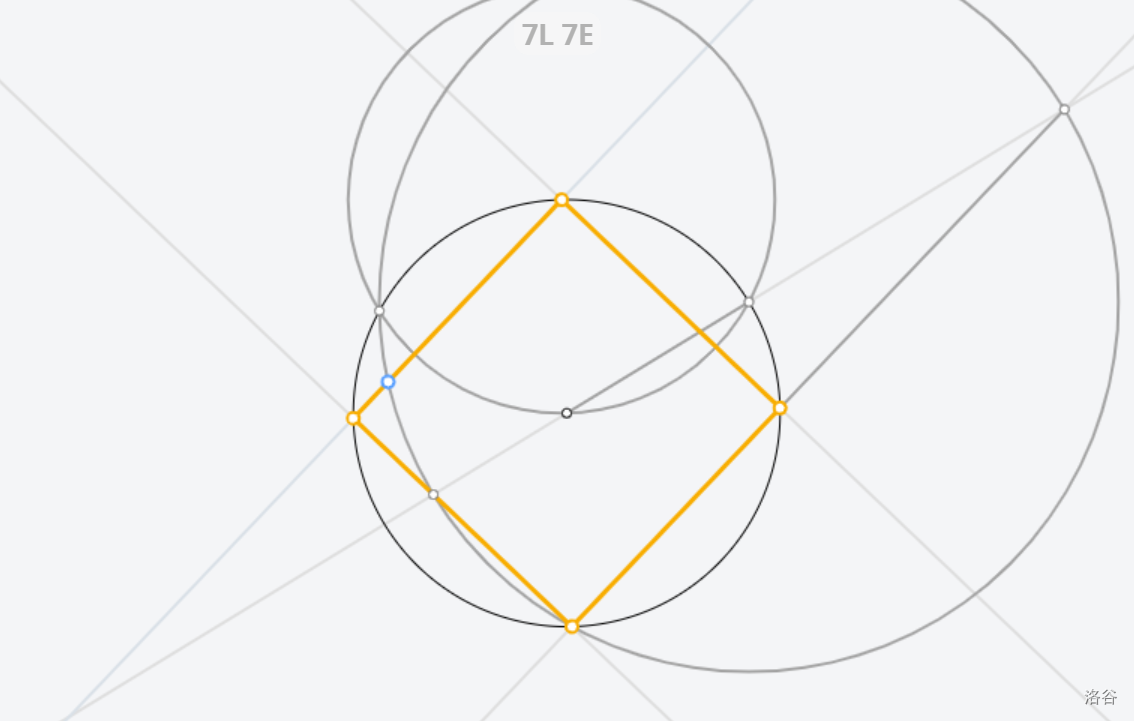

![](https://cdn.luogu.com.cn/upload/image_hosting/8x7bpsr6.png)

![](https://cdn.luogu.com.cn/upload/image_hosting/raxlrs73.png)

解释有点复杂，[见此](https://www.bilibili.com/video/BV1Bz4y1f7Rx/)。

## $\text{2. Beta}$

### $\text{2.1 角平分线}$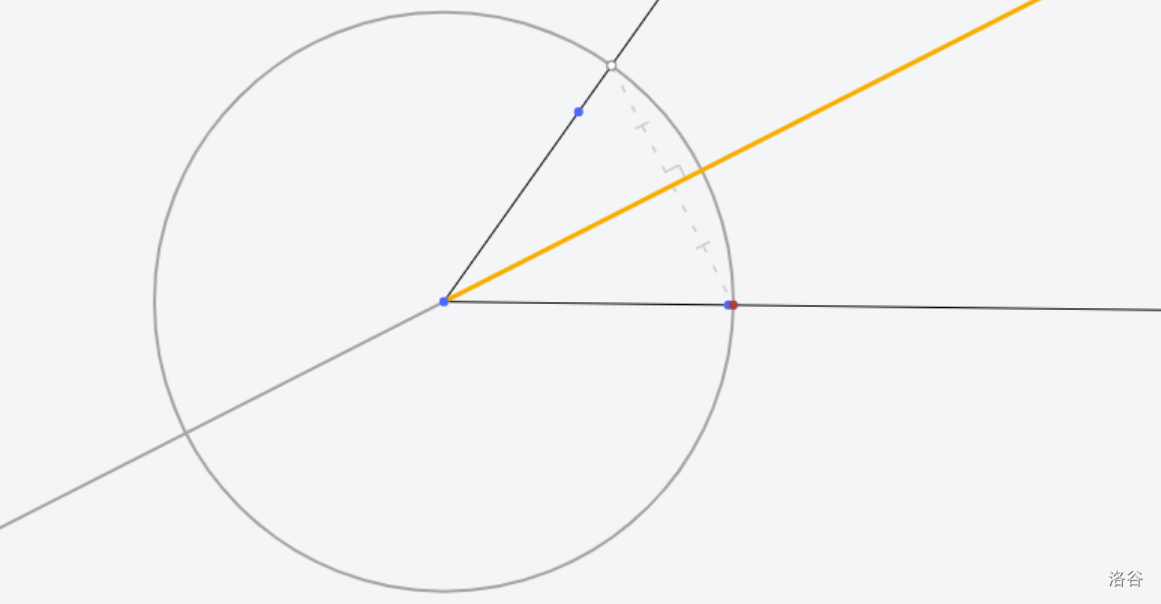

![](https://cdn.luogu.com.cn/upload/image_hosting/fwib9lgb.png)

做法：过顶点做圆，做圆与角两边连线的中垂线。

证明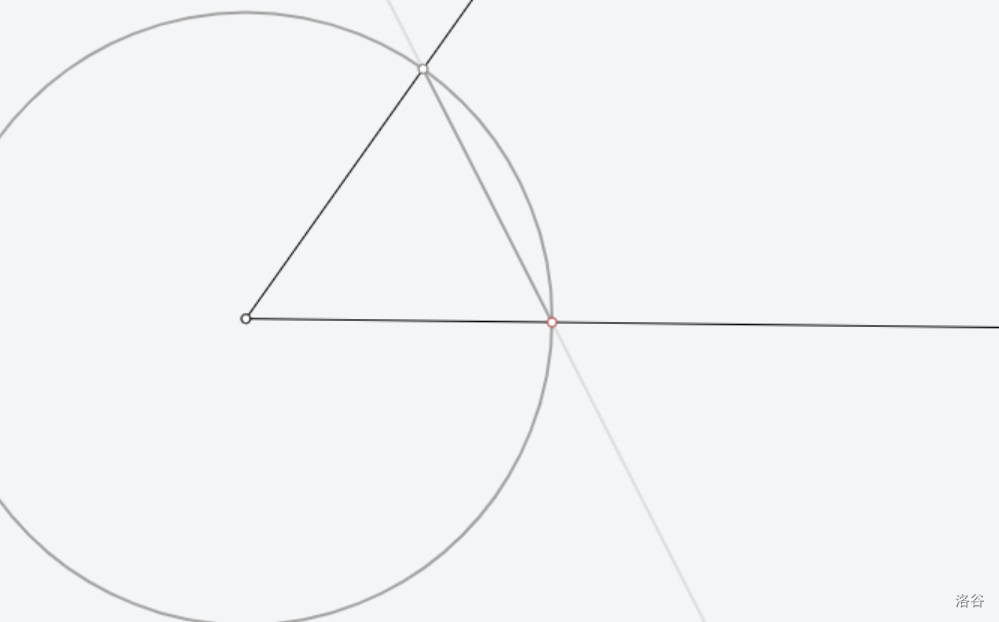

![](https://cdn.luogu.com.cn/upload/image_hosting/23t4ywyb.png)

这个三角形等腰，三线合一。

### $\text{2.* 角平分线工具}$

略。

### $\text{2.2 内心}$

gugugu……

正在渲染内容...