题解：P4751 【模板】动态 DP（加强版）

不知道为什么现在很多人觉得 Top Tree 很恶心？其实静态版本的它是很有优势的（动态的 SATT 常数太大了，不实用），尤其是在于维护信息不可减的时候。

## 静态 Top Tree 的优势

- 单 $\log$ 复杂度。
- 不需要额外用数据结构维护一个点轻儿子（虚儿子）的信息，以支持快速修改。
- 码量和全局平衡二叉树相当。
- 面对边权问题比其他做法更得心应手。

## 树收缩操作 & 树簇

Top Tree 的核心是两种树收缩操作：`Rake` 和 `Compess`。其中 `Compess` 将一个度数为 $2$ 的点的两条边合并，`Rake` 将一个度数为 $1$ 的点的边和另一条相邻边合并。给一张陈年老图：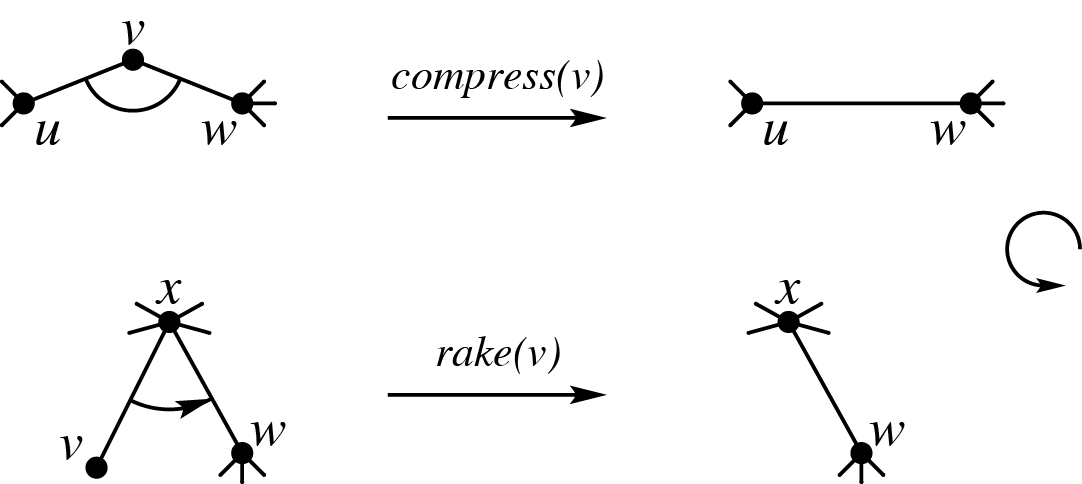

![](https://img.uoj.ac/user/negiizhao/basic.png)

这两种操作每次可以把两条边合成一条边，考虑进行若干次操作后一条边在原树中对应了什么：不难发现这一条边一定由原树中的一个边联通块合并而来，而且这个边连通块只有两个点与联通块外的点联通，我们称这一个连通块为一个**簇**，而两个与外界联通的端点为这个簇的上/下界点，这两个端点的路径构成了该簇的**簇路径**。下图给出了一个簇的形态，这个簇的端点是 $u,z$。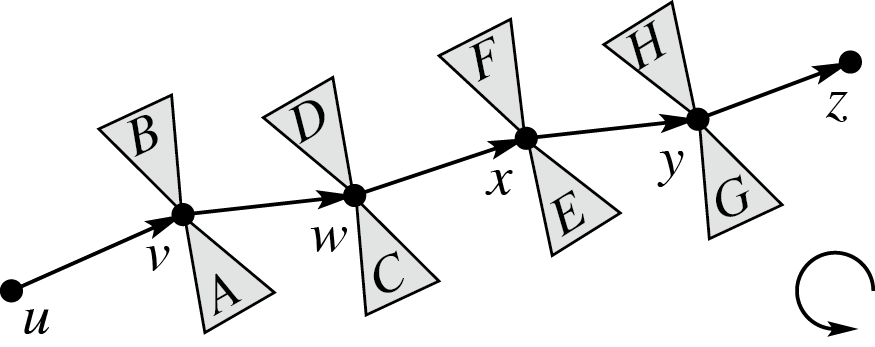

![](https://img.uoj.ac/user/negiizhao/sample0.png)

下图则给出了合并过程中的一条边 $(A,D)$ 所对应的簇形态：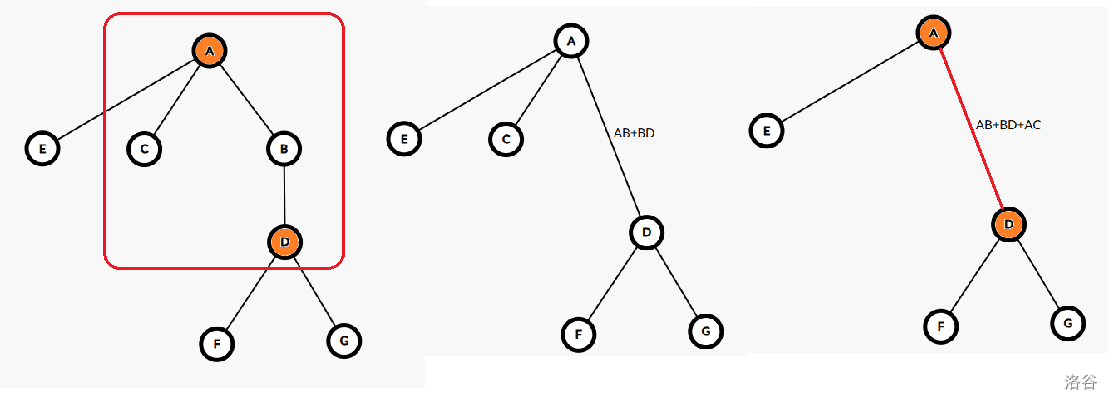

![](https://cdn.luogu.com.cn/upload/image_hosting/vflxv32o.png)

类似的，我们发现原树中的每一条边就是一个两点一边的簇，我们称这 $n-1$ 个簇为**基簇**。

## Top Tree

注意：不同“品种”的 Top Tree 在结构上略有差异，如 SATT 是一颗三叉树，拥有左中右三个儿子，但底层思想都是用树去描述树收缩过程。

发现每次 `Compess/Rake` 都会合并两个拥有一个公共点的簇（`Rake` 为上界点公共，`Compess` 为一个簇上界点与另一个簇的下界点公共），我们考虑将这个合并过程用一颗二叉树来表示，这个树的每一个叶子代表一个基簇，一个结点的两个儿子就表示这个当且结点对应的簇是由这两个儿子对应的簇合并而来，而当前点的类型（`Compess/Rake`）就表示这两个儿子是通过哪种树收缩操作合并而来。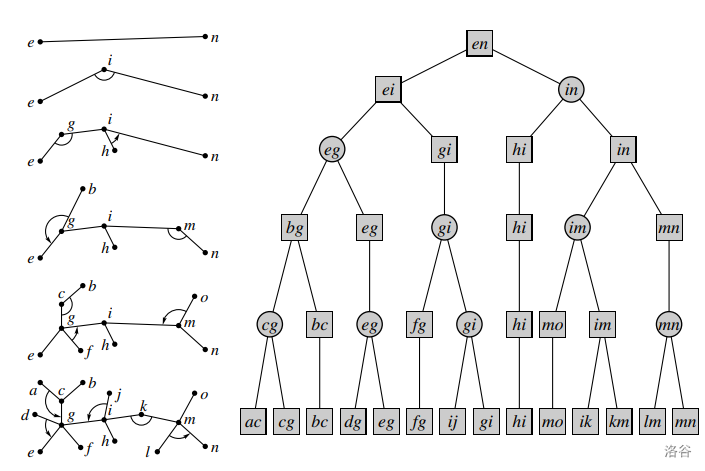

![](https://cdn.luogu.com.cn/upload/image_hosting/pvpx7u5s.png)

注意：由于簇的端点会同时位于多个簇中，一般我们只维护簇中边和非上界点的信息，体现在后面维护动态 DP 的代码上，就是记录上界点状态而不计算上界点贡献。

不难发现，一颗 $n$ 个叶子的二叉树（每个结点两个儿子），共有 $2n-1$ 个结点，结点总数可以接受。

这样子，更新一条边的信息，只需要从它的基簇开始跳 Top Tree 的父亲，每次二叉合并更新信息即可。这启示我们，如果我们可以找到一种收缩树的方式使其 Top Tree 的树高可以接受就可以快速维护信息了！

## 基于重量平衡的静态 Top Tree

对原树进行重链剖分。此时会发现 `Compess` 操作相当于重链上线段树的 `pushup`，而 `Rake` 就相当于将轻儿子信息合并入重链。

那么我们就有一个思路了，对于一个原树中的点和它的若干轻儿子，我们可以建立一棵 leafy 的类线段树结构（Rake Tree），去分治的将相邻两个结点用 `Rake` 操作合并，如将下图中的簇 $A,B,C,D$ 合并到 $(u,v)$ 这条边上。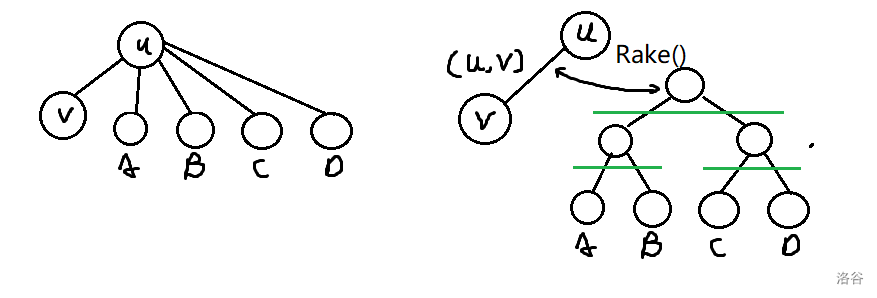

![](https://cdn.luogu.com.cn/upload/image_hosting/u3ge1wi4.png)

等我们将一条重链的所有轻儿子 `Rake` 到重链上后，此时我们再用一个 leafy 的类线段树结构（Compess Tree）将这些簇用 `Compess` 操作分治合并起来。至此，一条重链就被我们缩成了一个簇。

考虑这种算法的单次修改的复杂度：每条重链用一个 $\mathcal{O}(\log n)$ 去 `pushup`，共有 $\mathcal{O}(\log n)$ 条重链需要 `pushup`，总共 $\mathcal{O}(\log^2 n)$。

考虑优化，我们沿用全局平衡二叉树的思想，用每一个结点的簇大小作为分治区间的中点，此时每一个结点向上跳一或两次，其对应的簇大小至少翻倍，因此树高为 $\mathcal{O}(\log n)$，具体分析同全局平衡二叉树。

此时每一条原树上的边对应的基簇一定是这个 leafy 结构的叶子结点，从而修改边权就变得十分简单：直接 `Compess/Rake` 到根即可，而不需要在轻重儿子切换时做很多分讨。

## 常见可维护信息

显然，我们需要维护 `Compess` 和 `Rake` 两种 `pushup` 方式。

`Rake(x,y)` 默认是把 $y$ 往 $x$ 上合并。

- 簇大小：
  - `Compess(x,y)`：$sz=sz_x+sz_y$。
  - `Rake(x,y)`：$sz=sz_x+sz_y$。
- 簇路径长度：
  - `Compess(x,y)`：$len=len_x+len_y$。
  - `Rake(x,y)`：$len=len_x$。

通过这两个信息，相必你对 Top Tree 的合并操作有了更深入的理解。

## 维护动态 DP

明晰 Top Tree 只能维护边信息，如果像本题需要维护点信息，则需要将一个点的权值存到它的父亲边上，对于无父亲边的根，则新建虚根，使根存在父亲边（即点权上升为边权）。

通常，Top Tree 维护的 DDP 需要维护 $f_{x,0/1,0/1}$ 来记录上/下界点的状态，这是因为在合并两个簇的时候，这两个簇的公共点需要保证状态相同，而且需要统计跨越这两个簇的信息。

对于本题，设  $f_{x,0/1,0/1}$ 表示上下界点是否被选入独立集，此时簇内最大独立集大小即可解决问题。注意一个坑点：

- 我们只是记录上界点状态，而不计算上界点贡献，因为它会在当前簇的上面那个簇计算。

## Code

代码有注释。

```cpp
#include<bits/stdc++.h>
using namespace std;
namespace fast_IO{
#define ld cin
#define jyt cout
} using namespace fast_IO;
#define ll long long
#define ull unsigned long long
#define REP(i, l, r) for (int i = l; i <= r; ++i)
#define PER(i, l, r) for (int i = l; i >= r; --i)
#define bitcount(x) __builtin_popcount(x)
#define albit(x) ((1 << (x)) - 1)
#define mkbit(x) (1 << (x - 1))
#define gtbit(x, id) (((x) >> (id - 1)) & 1)
// #define ld cin
// #define jyt cout
// #define int long long
const int N = 2e6 + 7;
const int inf = 1e9 + 7;
namespace TopTree {
    struct Mat {ll o[2][2]; Mat() {memset(o, 0, sizeof(o));}};
    int a[N], fa[N], sz[N], son[N], dep[N], Cluster[N];
    vector<int> G[N];
    struct Data {int sz; Mat lxl; Data() {sz = 0, lxl = Mat();}}; // 维护的信息
    struct Node {
        int lc, rc, fa; char op; Data v;
#define ls(x) tr[x].lc
#define rs(x) tr[x].rc
#define fa(x) tr[x].fa
    } tr[N]; int Trc = 0;  
    inline Data Compess(Data &a, Data &b) {
        Data c;
        c.sz = a.sz + b.sz;
        c.lxl.o[0][0] = max(b.lxl.o[0][0] + a.lxl.o[0][0], b.lxl.o[0][1] + a.lxl.o[1][0]);
        c.lxl.o[1][0] = max(b.lxl.o[1][0] + a.lxl.o[0][0], b.lxl.o[1][1] + a.lxl.o[1][0]);
        c.lxl.o[0][1] = max(b.lxl.o[0][0] + a.lxl.o[0][1], b.lxl.o[0][1] + a.lxl.o[1][1]);
        c.lxl.o[1][1] = max(b.lxl.o[1][0] + a.lxl.o[0][1], b.lxl.o[1][1] + a.lxl.o[1][1]);
        return c;
    }
    inline Data Rake(Data &a, Data &b) {
        Data c;
        c.sz = a.sz + b.sz;
        c.lxl.o[0][0] = a.lxl.o[0][0] + max(b.lxl.o[0][0], b.lxl.o[1][0]);
        c.lxl.o[1][0] = a.lxl.o[1][0] + max(b.lxl.o[0][0], b.lxl.o[1][0]);
        c.lxl.o[0][1] = a.lxl.o[0][1] + max(b.lxl.o[0][1], b.lxl.o[1][1]);
        c.lxl.o[1][1] = a.lxl.o[1][1] + max(b.lxl.o[0][1], b.lxl.o[1][1]);
        return c;
    }
    inline Data init(int w) { // 初始化一个边权为 w 的基簇
        Data c; 
        c.sz = 1;
        c.lxl.o[0][0] = 0, c.lxl.o[0][1] = 0, c.lxl.o[1][0] = w, c.lxl.o[1][1] = -inf;
        return c;
    }
    inline int BaseCluster(int w) {return ++Trc, tr[Trc].op = 'B', tr[Trc].v = init(w), Trc;} // 创建一个基簇
    inline void pushup(int x) {tr[x].v = (tr[x].op == 'R' ? Rake : Compess)(tr[ls(x)].v, tr[rs(x)].v);}
    inline int Merge(int x, int y, char op) {return ++Trc, fa(tr[Trc].lc = x) = fa(tr[Trc].rc = y) = Trc, tr[Trc].op = op, pushup(Trc), Trc;} // 创立一个 op 类型的结点用于合并两个簇 x,y
    inline void Prework(int x, int p) {
        fa[x] = p, sz[x] = 1, dep[x] = dep[p] + 1; 
        for (int v : G[x]) if (v ^ p) Cluster[v] = BaseCluster(a[v]), Prework(v, x), son[x] = (sz[v] > sz[son[x]] ? v : son[x]), sz[x] += sz[v];
    }
    inline int build(vector<int> &node, int l, int r, char op) { // 分治的用 op 操作把 node 中的簇合成一个。
        if (l == r) return node[l];
        int mid = r - 1, psz = 0, allsz = 0;
        REP(i, l, r) allsz += tr[node[i]].v.sz;
        REP(i, l, r - 1) if ((psz += tr[node[i]].v.sz) * 2 >= allsz) {mid = i; break;}
        return Merge(build(node, l, mid, op), build(node, mid + 1, r, op), op);
    }
    inline int Build(int x) {
        vector<int> compess;
        if (Cluster[x]) compess.emplace_back(Cluster[x]);
        for (; son[x]; x = son[x]) {
            vector<int> rake;
            for (int v : G[x]) if (v ^ fa[x] && v ^ son[x]) rake.emplace_back(Build(v));
            if (!rake.size()) compess.emplace_back(Cluster[son[x]]);
            else compess.emplace_back(Merge(Cluster[son[x]], build(rake, 0, (int)rake.size() - 1, 'R'), 'R')); // 把合并完的轻儿子合到 (x,son[x]) 这条重边上
        }
        return build(compess, 0, (int)compess.size() - 1, 'C');
    }
    inline void Modify(int x, int y) { // 如你所见，修改非常简单。
        tr[Cluster[x]].v = init(a[x] = y);
        for (x = tr[Cluster[x]].fa; x; x = tr[x].fa) pushup(x);
    }
}
namespace JoKing {
    int n, q, TopRt = 0;
    signed main() { int u, v, LA = 0;
        ld >> n >> q, TopTree::G[n + 1].emplace_back(1), TopTree::G[1].emplace_back(n + 1);
        REP(i, 1, n) ld >> TopTree::a[i];
        REP(i, 2, n) ld >> u >> v, TopTree::G[u].emplace_back(v), TopTree::G[v].emplace_back(u);
        TopTree::Prework(n + 1, 0), TopRt = TopTree::Build(n + 1);
        REP(i, 1, q) ld >> u >> v, TopTree::Modify(u ^= LA, v), jyt << (LA = max(TopTree::tr[TopRt].v.lxl.o[0][0], TopTree::tr[TopRt].v.lxl.o[1][0])) << '\n';
        return 0; 
    }
}
signed main() {
#ifndef WYY
//	freopen("std.in", "r", stdin);
//	freopen("user.out", "w", stdout);
#endif
//	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    JoKing::main(); return 0;
}
```

## 拓展例题

建议去做 [[SDOI2017] 切树游戏](https://www.luogu.com.cn/problem/P3781)，这题把 Top Tree 不用支持删除轻儿子信息的优势发挥的很明显。

## 参考资料

~~Top Tree 学的人少可能就是因为资料太杂了吧~~。

- 图很清晰：[Top tree 相关东西的理论、用法和实现 negiizhao](https://negiizhao.blog.uoj.ac/blog/4912)。

- 代码实现清晰：[简单萌萌哒 Top Tree（上）Laijinyi](https://www.cnblogs.com/laijinyi/p/18373391/Top-Tree-1)。

- 侧重动态 Top Tree：[Top Tree OI Wiki](https://oi.wiki/ds/top-tree/)。

- 代码实现清晰：[Top Tree & Top Cluster 分块 Richardwhr](https://www.cnblogs.com/Richardwhr/p/18834468)。

- 适合初学：[浅谈 Top Tree jerry3128](https://www.luogu.com/article/rnzh9gqy)。

- 适合初学：[Top Tree 相关理论扯淡 ExplodingKonjac](https://www.cnblogs.com/ExplodingKonjac/p/17890636.html)（这篇不知道为什么会一直卡在加载界面，要 F12 把加载界面删掉才看得到）。

推荐一个 Top Tree 可视化：[link](https://maomao9-0.github.io/static-top-tree-visualisation/)。