搜索枚举_冯政玮

A - 循环赛

搜索剪枝

题面

$n$ 支队伍比赛，每两支队伍比赛一次，平 $1$ 胜 $3$ 负 $0$。

给出队伍的最终得分，求有多少种可能的分数表。

平1胜3负0指：

• 若两支队伍打平，则各得到 $1$ 分；
• 否则，胜利的队伍得到 $3$ 分，被打败的队伍得到 $0$ 分。

$n\le 8$

题解

搜索剪枝。

• 知道总分数，可以列方程知道平局数与胜局数，剪枝

• 如果有人的得分超过了总得分，剪枝

• 如果有人无论如何也达不到总得分，剪枝

• 当一个人被匹配完后，对剩下场数的状态进行记忆化，注意必须是当一个人匹配完后再记忆化，因为在匹配过程中，一个人同时受自己的剩下的场数及剩下的未匹配的人限制，比如一个人还剩 $5$ 场 $4$ 个人，与还剩 $5$ 场 $5$ 个人的方案是不一样的。

便可以通过。

方法

• 搜索剪枝

B - Binary Cards

简化搜索条件

题面

给定 $a_{1\sim n}$ 让你构一个最短的序列，使得这个序列的子集和可以表示出这 $n$ 个数，这个序列的元素要求一定是 $\pm 2^k$

$n,a_i\le 2\times 10^5$

题解

注意到以下操作不会使得答案更劣

• $a,a → a,2a$ 。

• $-a,a\to -a,2a$

所以对于一个 $k$，$\pm2^k$ 不会同时存在，

如果 $\forall i, 2|a_i$，就一定不会选择 $\pm1$ 否则就一定选择其中一个。

所以可以对于所有数，判断是否被 $2$ 整除。是则递归进下一个 $k$ 否则枚举是选 $1$ 还是 $-1$,并将所有不能被 $2$ 整除的数（需要这个 $1$ 的数）减去这个数再除以二，递归进入下一个 $k$。

由于每次值域减半，每次去重后再处理，复杂度 $T(n)=2T(\frac n2)+n,\mathcal O(n\log n)$

方法

• 简化搜索条件，使得可能性减少。

D - Balanced Cow Subsets G

折半搜索

题面

$n\le 20$ 个数， 求有多少个子集，满足这个子集能被划分成两个不交的部分，使得这两个部分和相同。

题解

每个数有划分至左、右以及不选择三中情况，可以搜索，我们可以将条件看作 $w=左部集合-右部集合=0$。

发现 $3^{20}$ 次方过不了，$3^{10}$ 可过，考虑折半搜索。

记录前 $\frac n2$ 个数的$w$对应哪些方案（这里应该去重否则遍历一次会从$\mathcal O(2^{\frac n2})$变为$\mathcal O(3^{\frac n2})$），当右边有一个 $-w$ 时，进行匹配，最后去重。

时间复杂度：$\mathcal O(w6^{\frac n2})$，去重用unordered_set实现，$w=10$ ，去重用bitset实现，$w=\frac 1{64}$

方法

• 折半搜索

F - 靶形数独

搜索剪枝

题面

靶形数独的方格同普通数独一样，在 9 格宽且 9 格高的大九宫格中有 9 个 3 格宽且 3 格高的小九宫格（用粗黑色线隔开的）。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。如左图：

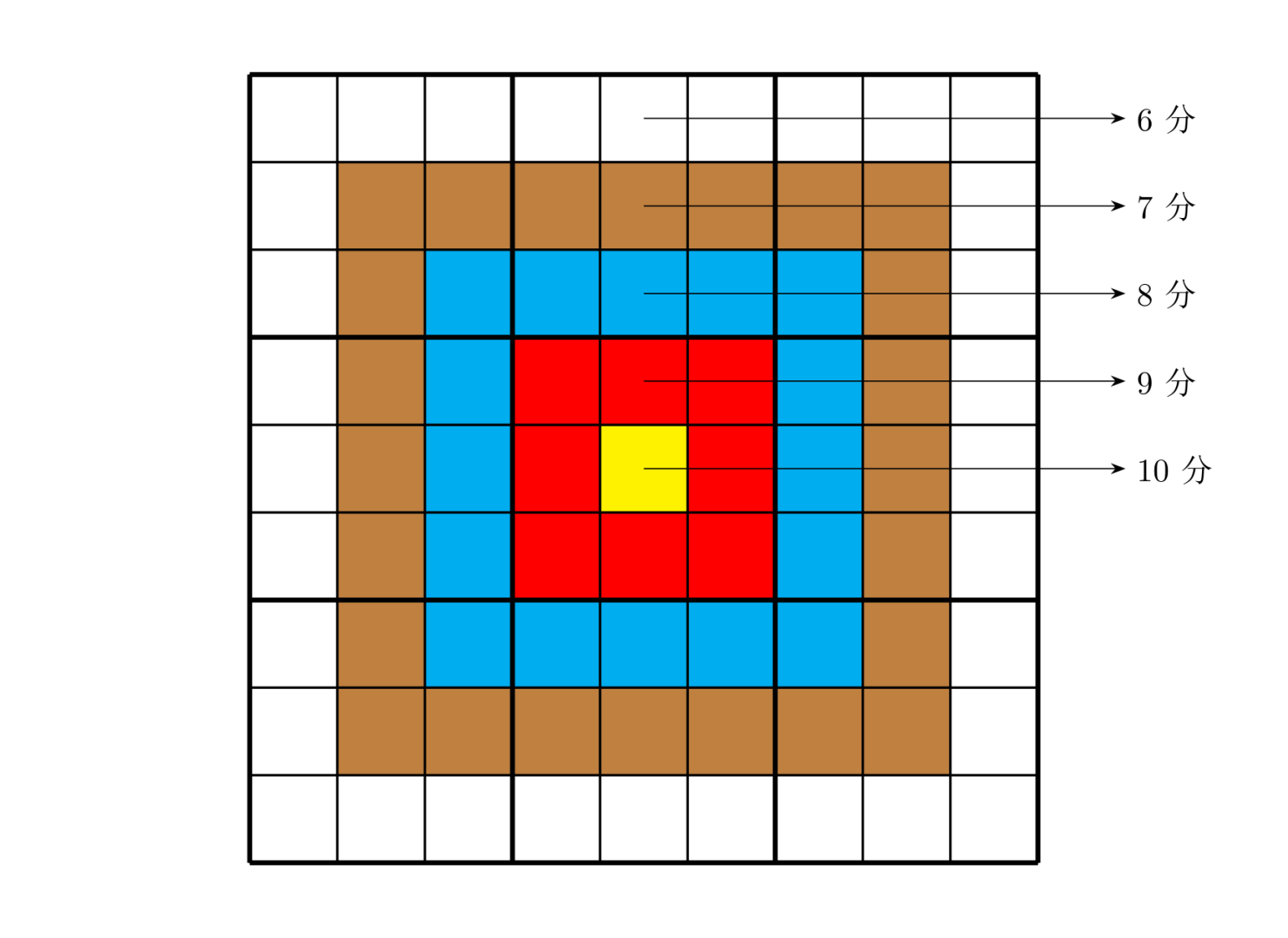
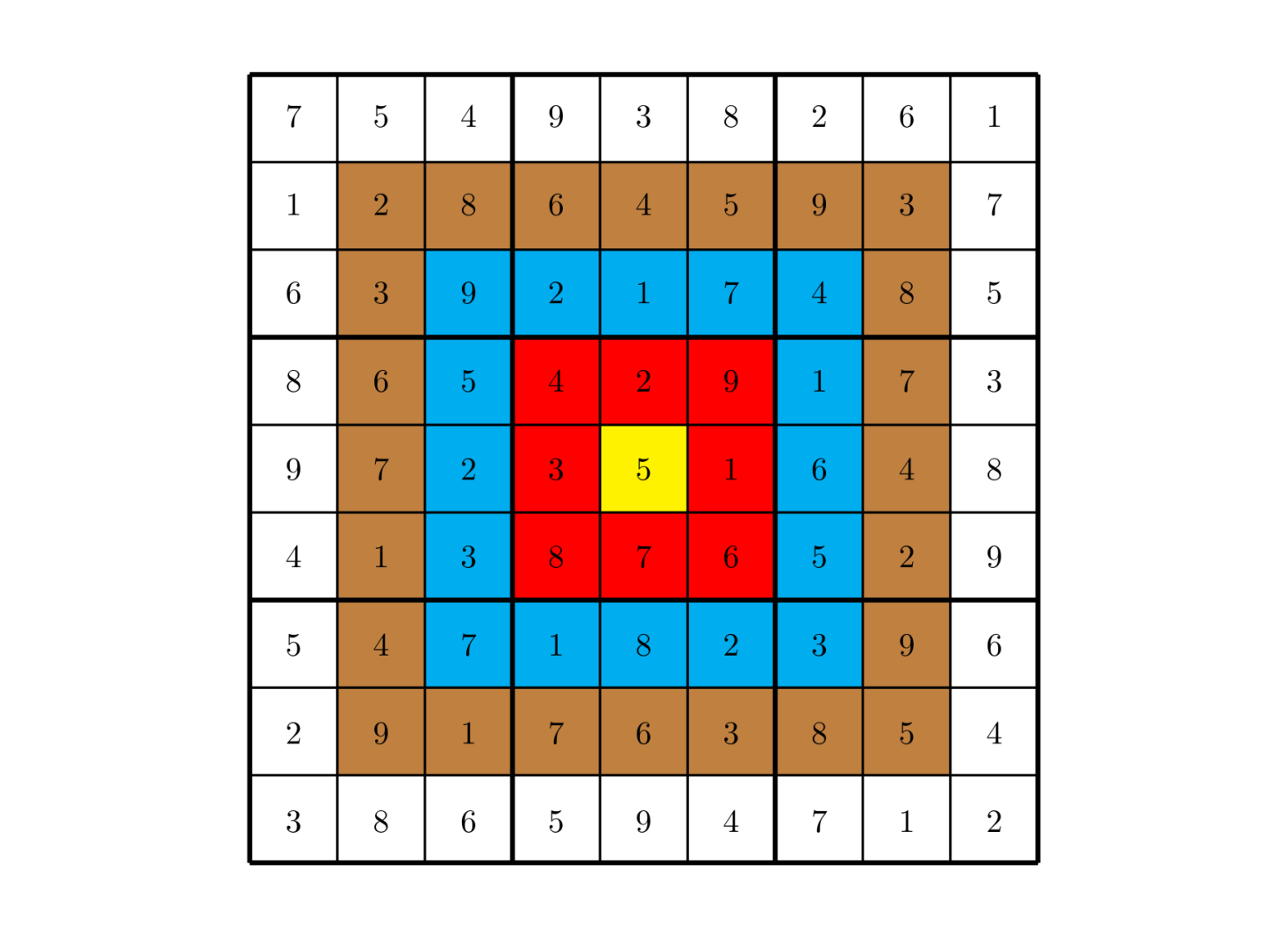
总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如右图，在以下的这个已经填完数字的靶形数独游戏中，总分数为 $2829$。

给定一个已经填了$m$个数的数独，求其最大分数，无解输出 $-1$。

$m\ge 24$

题解

搜索剪枝，让 $0$ 少的行先被搜索填充，可以尽早判断是否合法。

方法

• 搜索剪枝——尽早判断不合法

G - Au Pont Rouge

题面

给出一个长度为 $n$ 的字符串 $S$ 以及整数 $m,k$。

对于一个把 $S$ 分割成非空的 $m$ 段的一个方案，我们用这个方案中分割出的字典序最小的一个串代表这个分割方案。

现在把所有分割方案对应的代表该方案的串按字典序从大到小排序，求排序后的第 k 个串。

$1\le m\le n\le 1000,1\le k\le 10^{18}$

题解

直接求代表元素不好求，可以考虑转化为判定，先将所有子串排序，二分判定大于串 $S$ 的划分方式有几个。

首先是如何快速比较子串

令 $lcp_{x,y}=\operatorname{lcp}(s[x\sim n],s[y\sim n])$，有

$$ lcp_{x,y}= \left{\begin{aligned} &lcp_{x+1,y+1}+1&&s_x=s_y\ &0&&s_x\not=s_y \end{aligned}\right. $$

可以 $\mathcal O(n^2)$ 求出。

比较两个子串 $s[l_1\sim r_1]$ 与 $s[l_2\sim r_2]$。

• 若 $lcp_{l_1,l_2}\ge \min(r_1-l_1+1,r_2-l_2+1)$，直接比较子串长度。

• 否则比较 $s[l_1+lcp_{l_1,r_1}]$ 与 $s[l_2+lcp_{l_1,l_2}]$

于是我们可以 $\mathcal O(1)$ 比较。

排序复杂度 $\mathcal O(n^2\log n)$

接着如何求解划分个数

令 $dp_{i,j}$ 表示将 $s[1\sim i]$ 划分为 $j$ 段且每一段的字典序都大于 $S$ 的方案数，有：

$$ dp_{i,j}=\sum_{(t \leq i)\land(s[t\sim i]>S)}dp_{t-1,j-1} $$

在每次转移的时候都需要枚举 $t$，复杂度 $\mathcal O(n^3)$。

我们知道字典序是从前往后比较的，但这个方程中却在不断移动左端点，使得我们不得不重新得到大小信息，于是可以考虑从后往前转移。

令 $dp_{i,j}$ 表示将 $s[i\sim n]$ 划分为 $j$ 段且每一段的字典序都大于 $S$ 的方案数，有：

$$ dp_{i,j}= \sum_{(t\ge i)\land(s[i\sim t]>S)}dp_{t+1,j-1} $$

根据我们对于子串比较的分析，

$$ \exist w,s[i\sim w]>S\implies\forall t\in[w,n],s[w\sim n]>S $$

这样就可以$\mathcal O(n^2)$ 转移了，加上二分，复杂度$\mathcal O(n^2\log n)$

总复杂度 $\mathcal O(n^2\log n)$

方法

• 预处理快速比较子串

• 更改枚举顺序——字典序尽量保证左端点定而右端点动

H - Wavy numbers

题面

我们将一类正整数称为“波浪数”，它的每个数位上的数都大于或小于两边数位上的数。

你的任务是找到第 $k$ 小的能被 $n$ 整除的波浪数 $r$。

$1\le k,n,r\le 10^{14}$

题解

注意到 $\sqrt {10^{14}}=10^7$ 是可以接受的，我们考虑折半搜索。

具体地，搜索两个数 $a,b$ 满足 $a,b< 10^7,a\times 10^7+b\equiv 0\pmod n$

可以先枚举 $b$ ，如果 $r$ 是在这里面的，直接输出答案。并当 $b$ 在整个 $7$ 位上都是“波浪的”，那么保存 $b\mod n$ 的余数，以便处理枚举 $a$ 时的情况。

但是如果在枚举 $a$ 的时候直接用 unordered_map 常数太大，可以先用其处理，处理完 $b$ 后经行离散化，在整个 $7$ 位上都是“波浪数”的个数大小不会超过 $900000$，接着用数组存储即可。

方法

• 假数位DP，真折半搜索