前缀和

定义

前缀和可以简单理解为 $\lceil$ 数列的前 $n$ 项的和 $\rfloor$，是一种重要的预处理方式，能大大降低查询的时间复杂度。

例题

有 $n$ 个的正整数放到数组 $a$ 里，现在要求一个新的数组 $b$，新数组的第 $i$ 个数 $b_i$ 是原数组 $a$ 第 $1$ 到第 $i$ 个数的和。

输入

5
1 2 3 4 5

输出

1 3 6 10 15

解题思路 递推：B[1]=A[1]，对于 $i\ge 2$ 则 B[i]=b[i-1]+A[i]。 参考代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],b[N];

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	// 前缀和数组的第一项和原数组的第一项是相等的。
  	b[1] = a[1];
  	for (int i = 2; i <= n; i++) {
		// 前缀和数组的第 i 项 = 原数组的 0 到 i-1 项的和 + 原数组的第 i 项。
		b[i] = b[i - 1] + a[i];
  	}
  	for (int i = 1; i <= n; i++) {
		cout << b[i] << " ";
  	}
   	return 0;
}

二维/多维前缀和

常见的多维前缀和的求解方法有两种。

• 基于容斥原理

  这种方法多用于二维前缀和的情形。给定大小为 $m\times n$ 的二维数组 $a$，要求出其前缀和 $s$。那么，$s$ 同样是大小为 $m\times n$ 的二维数组，且

  $$s_{i,j}\gets\begin{aligned} \sum_{i'\leq i}\end{aligned}\begin{aligned} \sum_{j'\leq j}\end{aligned}A_{i',j'}$$

  类比一维的情形，$s_{i,j}$ 应该可以基于 $s_{i-1,j}$ 或 $s_{i,j-1}$ 计算，从而避免重复计算前面若干项的和。但是，如果直接将 $s_{i-1,j}$ 和 $s_{i,j-1}$ 相加，再加上 $a_{i,j}$，会导致重复计算 $s_{i-1,j-1}$ 这一重叠部分的前缀和，所以还需要再讲这部分减掉。这就是 容斥原理。由此得到如下递推关系：

  $$s_{i,j}=a_{i,j}+s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1}$$

  实现是，直接遍历 $(i,j)$ 求和即可。

  

  有 $$s_{3,3}=a_{3,3}+s_{2,3}+s_{3,2}-s_{2,2}=5+18+15-9=29$$

  可以在 $O(1)$ 时间内完成。

• 逐维前缀和

  对于一般的情形，给定 $k$ 维数组 $a$，大小为 $n$，同样要求得其前缀和 $s$。这里，

  $$s_{i_1,\cdots,i_k}=\begin{aligned} \sum_{i'_1\le i_1}\end{aligned}\cdots\begin{aligned} \sum_{i'_k\le i_k}\end{aligned}a_{i'_1,\cdots,i'_k}$$.

  从上式可以看出，$k$ 维前缀和就等于 $k$ 次求和。所以，一个显然的算法是，每次只考虑一个维度，固定所有其它维度，然后求若干个一维前缀和，这样对所有 $k$ 个维度分别求和之后，得到的就是 $k$ 维前缀和。

  提供一个3维的高维前缀和参考代码：

  int a[n+1][n+1][n+1],b[1<<n];
  int fun(int i,int j,int k){
  	return i*4+j*2+k;
  }
  int main(){
  	//高维前缀和
  	for(int i=2;i<=n;i++)
  		for(int j=1;j<=n;j++)
  			for(int k=1;k<=n;k++)
  				a[i][j][k]+=a[i-1][j][k];
  	for(int i=1;i<=n;i++)
  		for(int j=2;j<=n;j++)
  			for(int k=1;k<=n;k++)
  				a[i][j][k]+=a[i][j-1][k];
  	for(int i=1;i<=n;i++)
  		for(int j=1;j<=n;j++)
  			for(int k=2;k<=n;k++)
  				a[i][j][k]+=a[i][j][k-1];
    //等价于
  	for(int i=2;i<=n;i++)
  		for(int j=1;j<=n;j++)
  			for(int k=1;k<=n;k++)
  				b[fun(i,j,k)]+=b[fun(i-1,j,k)];
  	for(int i=1;i<=n;i++)
  		for(int j=2;j<=n;j++)
  			for(int k=1;k<=n;k++)
  				b[fun(i,j,k)]+=b[fun(i,j-1,k)];
  	for(int i=1;i<=n;i++)
  		for(int j=1;j<=n;j++)
  			for(int k=2;k<=n;k++)
  				b[fun(i,j,k)]+=b[fun(i,j-1,k)];
  	//等价于
  	for(int h=1<<(n-1);h>0;h>>=1)
  		for(int i=0;i<1<<n;i++)
  			if(i&h)
  				b[i]+=b[i-h];
  	return 0;
  }
  

  因为考虑每一个维度的时候，都只遍历了整个数组一遍，这样的算法复杂度是 $O(k\cdot N)$ 的，通常可以接受。

树上前缀和

设 $sum_i$ 表示结点 $i$ 到根节点的权值总和。 然后：

• 若是点权，$x,y$ 路径上的和为 $sum_x+sum_y-sum_{lca}-sum_{fa_{lca}}$。
• 若是边权，$x,y$ 路径上的和为 $sum_x+sum_y-2\cdot sum_{lca}$。
  $\operatorname{LCA}$ 的求法参见 最近公共祖先。

差分

解释

差分是一种和前缀和相对的策略，可以当做是求和的逆运算。

这种策略的定义是令 $b_i = \begin{cases} a_i - a_{i-1} & i \in [2,n] \\ a_1 & i=1 \end{cases}$

性质

• $a_i$ 的值是 $b_i$ 的前缀和，即 $a_n = \begin{aligned} \sum_{i=1}^n\end{aligned}b_i$
• 计算 $a_i$ 的前缀和 $sum = \begin{aligned} \sum_{i=1}^n\end{aligned}a_i=\begin{aligned} \sum_{i=1}^n\end{aligned}\begin{aligned} \sum_{j=1}^i\end{aligned}b_j=\begin{aligned} \sum_{i=1}^n\end{aligned}(b-i+1)b_i $

它可以维护多次对序列的一个区间加上一个数，并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。

树上差分

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想了。

树上差分通常会结合 最近公共祖先 来进行考察。树上差分又分为 点差分 与 边差分，在实现上会稍有不同。

点差分

举例：对树上的一些路径 $\delta(s_1,t_1), \delta(s_2,t_2), \delta(s_3,t_3)\dots$ 进行访问，问一条路径 $\delta(s,t)$ 上的点被访问的次数。

对于一次 $\delta(s,t)$ 的访问，需要找到 $s$ 与 $t$ 的公共祖先，然后对这条路径上的点进行访问（点的权值加 $1$），若采用 DFS 算法对每个点进行访问，由于有太多的路径需要访问，时间上承受不了。这里进行差分操作：

$$d_s\gets d_s+1$$ $$d_{lca}\gets d_{lca}-1$$ $$d_t\gets d_t+1$$ $$d_{father(lca)}\gets d_{father(lca)}-1$$

其中 $father(x)$ 表示 $x$ 的父亲结点，$d_i$ 为点权 $a_i$ 的差分数组。

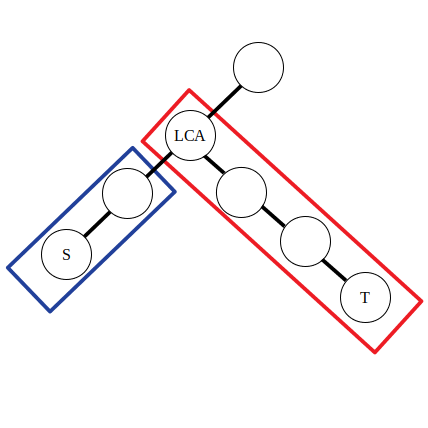
可以认为公式中的前两条是对蓝色方框内的路径进行操作，后两条是对红色方框内的路径进行操作。不妨令 $\textit{lca}$ 左侧的直系子节点为 $\textit{left}$。那么有 $d_{\textit{lca}}-1=a_{\textit{lca}}-(a_{\textit{left}}+1)，d_{f(\textit{lca})}-1=a_{f(\textit{lca})}-(a_{\textit{lca}}+1)$。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。

边差分

若是对路径中的边进行访问，就需要采用边差分策略了，使用以下公式：

$$d_s\gets d_s+1$$ $$d_t\gets d_t+1$$ $$d_{lca}\gets d_{lca}-2$$

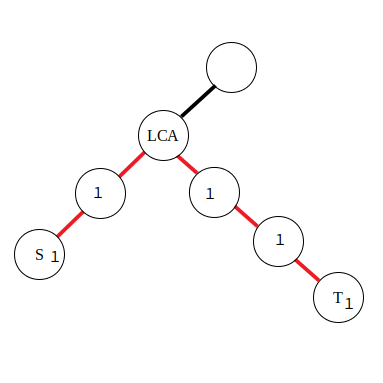
由于在边上直接进行差分比较困难，所以将本来应当累加到红色边上的值向下移动到附近的点里，那么操作起来也就方便了。对于公式，有了点差分的理解基础后也不难推导，同样是对两段区间进行差分。

例题

洛谷P3128

解题思路

需要统计每个点经过了多少次，那么就用树上差分将每一次的路径上的点加一，可以很快得到每个点经过的次数。这里采用倍增法计算 LCA，最后对 DFS 遍历整棵树，在回溯时对差分数组求和就能求得答案了。

参考代码

#include<bits/stdc++.h>
#define endl '\n'

using namespace std;
const int N=5e4+10,L=20;
int n,m,fa[N][L],dep[N],cnt[N],ma,k,pre[N],lg[N];

struct node{
	int to;
	int next;
}a[2*N];

void add(int u,int v){//建边
	a[++k]={v,pre[u]};
	pre[u]=k;
	return ;
}

void init(){//预处理log2
	lg[1]=0;
	for(int i=2;i<=n;i++)
		lg[i]=lg[i>>1]+1;
	return ;
}

void dfs(int x,int fath){//求深度、父亲结点
	dep[x]=dep[fath]+1;
	fa[x][0]=fath;
	for(int i=pre[x];i;i=a[i].next){
		int to=a[i].to;
		if(to!=fath){
			dfs(to,x);
		}
	}
	return ;
}

int lca(int u,int v){//求lca
	if(dep[u]<dep[v]) swap(u,v);
	while(dep[u]!=dep[v]){
		u=fa[u][lg[dep[u]-dep[v]]];
	} 
	if(u==v) return u;
	for(int i=L-1;i>=0;i--){
		if(fa[u][i]!=fa[v][i]){
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	return fa[u][0];
}

void dfs2(int x,int fath){
	for(int i=pre[x];i;i=a[i].next){
		int to=a[i].to;
		if(to!=fath){
			dfs2(to,x);
			cnt[x]+=cnt[to];//差分后前缀和操作
		}
	}
	ma=max(ma,cnt[x]);
	return ;
}

signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1,x,y;i<n;i++){
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	
	init();
	
	dfs(1,0);
	
	//倍增法求lca
	for(int j=1;j<L;j++){
		for(int i=1;i<=n;i++){
			fa[i][j]=fa[fa[i][j-1]][j-1];
		}
	}
	
	for(int i=1,x,y;i<=m;i++){
		scanf("%d%d",&x,&y);
		int lc=lca(x,y);
		//差分
		cnt[x]++;
		cnt[y]++;
		cnt[lc]--;
		cnt[fa[lc][0]]--;
	}
	
	dfs2(1,0);
	
	printf("%d",ma);
	return 0;
}